Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелінійні регресії 1-го класуСтр 1 из 4Следующая ⇒
Поліноміальна модель Степенева функція виду Y = а0 + а1 Х1 + а 2 Х 2 +... + а т Х т + u, що часто характеризує ту чи іншу економічну залежність можна звести до лінійної регресійної моделі. Заміняючи X на Х1, X2 на Х2,..., Хт на Хт, одержимо модель множинної лінійної регресїі із т змінними Х1, Х2, …, Хт: Y = а 0 + а 1 Х1 + а2 X2 +... + а mXm + u, параметри якої знаходяться за МНК (за допомогою статистичної функції «ЛИНЕЙН»). При цьому для оцінювання тісноти лінійного зв’язку можна використовувати лінійний коефіцієнт кореляції. · Кубічна функція Y = а0 + а1X + а2 Х 2 + а 3 Х 3 + u у мікроекономіці моделює залежність загальних витрат ТС від об'єму випуску Q (рис. 3,а). · Аналогічно квадратична функція Y = а0 + а1Х + а2 Х 2 + u може характеризувати залежність між об'ємом випуску Q і середніми (АС)або граничними (МС) витратами (рис.3, б); або між витратами на рекламу C і прибутком π (рис.3, в) тощо.
Рис.3 Гіперболічна модель Гіперболічна модель у загальному випадку має такий вигляд: Y = a0 + a1 · Її можна звести до лінійної регресійної моделі, заміняючи 1/ X на Z. Графіки гіперболічних моделей визначаються знаками параметрів â0, â1. · â0 < 0, â1 > 0: на рис. 4 зображена так звана крива Філліпса.
Рис. 4 · При â0 > 0, â1 > 0 крива залежності між факторними ознаками Y та X набуде вигляду:
Рис.5 Така залежність, що зображена на рис. кривою, має місце при дослідженні зв'язку між середніми фіксованими витратами Y і обсягом випуску продукції X.
· â0 > 0, â1 < 0: кpива залежності між змінними Y та X набере вигляду:
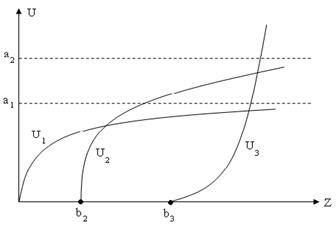
Рис.6 Зображена функція – це функція Торнквіста, за допомогою якої описується залежність між попитом Y на товари першої необхідності й доходом X. Шведський економіст П.Торнквіст запропонував спеціальні функції попиту для груп товарів першої, другої необхідності, предметів розкоші (рис. 7):
Рис. 7. Функції Торнквіста
· ·
· Нелінійні регресії 2-го класу Показникова моделі Модель Y = аеβх досить широко застосовується в економетричному аналізі. Найбільш важливим її застосуванням є ситуація, коли аналізується зміна фактора Y із постійним темпом приросту в часі: X символічно заміняється змінною t: Y = а еβt. Степенева модель Нехай деяка економічна залежність моделюється формулою Y = а0 Х а1 (*), де а0 і а1 - параметри моделі, що підлягають визначенню. Ця функція може характеризувати: · залежність попиту Y на благо від його ціни X (у цьому випадку (а1 < 0) або від доходу X (у цьому випадку а1 > 0); при такій інтерпретації змінних X і Y функція називається функцією Енгеля; · залежність обсягу випуску Y від використання ресурсу X (виробнича функція), 0 < а1 < 1.
Модель (*) не є лінійною функцією відносно X (похідна залежної змінної Y по X, щовказує на зміну Y щодо зміни X, буде залежати від X: Стандартним підходом до аналізу функцій даного роду в економетриці є логарифмування за експонентою е: 1п Y =1п а0 + а1 ln X. Після заміни 1п а0 = βо, а1 = β церівняння (6) матиме вигляд 1п Y = βо + β· lnX.
З метою статистичної оцінки коефіцієнтів введемо до моделі випадкову похибку u й одержимо так звану подвійну логарифмічну модель (і залежна, і пояснююча змінна задані в логарифмічному вигляді): 1п Y = β0 + β ln Х + u. Дане рівняння є лінійним відносно 1п Х і 1п Y, а також щодо параметрів β0 і β. Вводячи заміни Y* = 1п Y і Х* = 1пХ, цю модель можна переписати у вигляді: Y* = βо + β Х* + u. Отримана модель є лінійною моделлю. Якщо всі необхідні передумови класичної лінійної регресійної моделі для неї виконуються, то за МНК («ЛIНIЙН») можна визначити незміщені оцінки коефіцієнтів βо і β. Але при цьому коефіцієнт детермінації розраховується не для фактичних зміннихYі Х, а для їх логарифмів. Тобто для оцінювання якості розрахованої моделі потрібно додатково розрахувати коефіцієнти детермінації:
R2 = 1 - Коефіцієнт β є константою, яка характеризує сталу, тобто процентну зміну Y для даної процентної зміни X. Тому найчастіше подвійна логарифмічна модель називається моделлю постійної еластичності. Дійсно, продиференціювавши ліву й праву частини (7) по X, отримаємо:
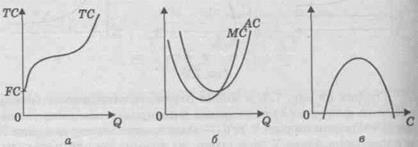
Дана модель легко узагальнюється на більшу кількість змінних. Наприклад, 1п Y = β0 + β1 lnX1 + β 2 lnX2 + u. Тут коефіцієнти β 1, β2 є еластичностями змінної Y за змінними X1 і Х2 відповідно. Напівлогарифмічні моделі Моделі виду Ln Y = βо + βХ + u, (**), Y = βо + β lnХ + u (***) називаються напівлогарифмічними моделями. Лог - лінійна модель Напівлогарифмічна модель (**) легко зводиться до лінійної моделі заміною Y* = 1пY. Коефіцієнт β y моделі (**) характеризує темп приросту змінної Y по змінній X, тобто характеризує відношення відносної зміни Y до абсолютної зміни X. Дійсно, продиференціювавши (**) по X, маємо:
Помноживши β на 100, одержимо процентну зміну змінної Y (темп приросту змінної Y). Тому напівлогарифмічна модель (**) зазвичай використовується для вимірювання темпу приросту економічних показників: наприклад, при аналізі банківського вкладу за первісним внеском й процентною ставкою, при дослідженні залежності приросту об'єму випуску від відносного (процентного) збільшення витрат ресурсу, бюджетного дефіциту від темпу росту ВНП, темпу росту інфляції від об'єму грошової маси тощо. До такої моделі зводиться залежність, відомa в банківському й фінансовому аналізі: Yt = Y0 (1 + r) t, де Yо - початкова величина змінної Y (наприклад, первісний внесок у банку); r - складний темп приросту величини Y (процентна ставка); Yt - значення величини Y нa момент часу t (внесок дo банкy нa момент часу t). Прологарифмувавши попередній вираз маємо: 1п Yt = 1п Y0 + t ·1п(1 + r). Уведемо позначення: 1п Y 0 = β0 , 1п(1 + r) = β. Тоді отримаємо таку модель: 1п Yt = β0 + β t + u t. В цій моделі використали додатково випадковий доданок u t (вразі можливої мінливості процентної ставки). Крім того, співвідношення β = 1п(1 + r) визначає темп приросту r показника Y: 1 + r = eβ, r = 1 - eβ. При цьому коефіцієнт β визначає миттєвий темп приросту, а коефіцієнт r – узагальнений (складний) темп приросту величини Y.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.81.94 (0.021 с.) |
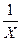 + u.
+ u. Модель Y = a0 + a1 ·
Модель Y = a0 + a1 · 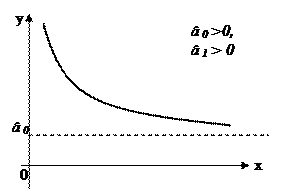
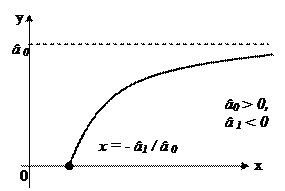
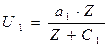 - функція Торнквіста для товарів I необхідності: зростання попиту на першочергові товари зі зростанням доходу поступово уповільнюється і має границю
- функція Торнквіста для товарів I необхідності: зростання попиту на першочергові товари зі зростанням доходу поступово уповільнюється і має границю 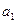 (крива попиту асимптотично наближається до прямої
(крива попиту асимптотично наближається до прямої 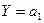 );
); , де
, де 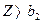 - функція Торнквіста на товари II необхідності має свою границю
- функція Торнквіста на товари II необхідності має свою границю 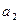 більш вищого рівня (
більш вищого рівня (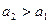 ), причому попит на групу цих товарів з’являється лише за умови досягнення доходу рівня
), причому попит на групу цих товарів з’являється лише за умови досягнення доходу рівня 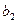 ;
;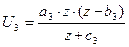 , де
, де 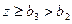 - функція Торнквіста для предметів розкошу: не має границі, і попит на ці товари виникає тільки за умови підвищення доходу рівня
- функція Торнквіста для предметів розкошу: не має границі, і попит на ці товари виникає тільки за умови підвищення доходу рівня  і далі зростає дуже швидко.
і далі зростає дуже швидко.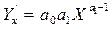 ),тобто не буде константою, що властиве лише нелінійним моделям.
),тобто не буде константою, що властиве лише нелінійним моделям.



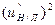
 =
= 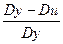 , Dу =
, Dу =  ,
, 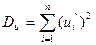 =
=  .
.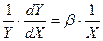 ,
, 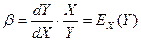
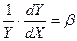 ,
,