Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность гипотез. Формула Бейеса ⇐ ПредыдущаяСтр 3 из 3
Пусть событие А может наступить при условии появления одного из несовместных событий Blt Ва,..., Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности Р (А) = Р (В1) PВ1 (A)+ P (В2) РB2 (A) +.. + P (Вn) РBn (A) Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности Найдем сначала условную вероятность РА (В1). По теореме умножения имеем Р (AB1) = Р (A) РА (В1) = Р (В1) PB1 (A). Из двойного равенства получим Р (A) РА (В1) = Р (В2) PB1 (A). Итак, РА (В1) = (Р (В1)· PB1 (A)): Р (A) или РА (В1) = (Р (В1)· PB1 (A)): (В1) PВ1 (A)+ P (В2) РB2 (A) +.. + P (Вn) РBn (A))
Аналогично определяющие условные вероятности остальных гипотез, Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Задания 4-9 1. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму - 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым - 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер. Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения: 1) деталь проверил первый контролер (гипотеза B1)', 2) деталь проверил второй контролер (гипотеза В2). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса: РА (В1) = (Р (В1)· PB1 (A)): (В1) PВ1 (A)+ P (В2) РB2 (A) +.. + P (Вn) РBn (A)) *** По условию задачи имеем: P(B1)= 0,6 -вероятность того, что деталь попадает к первому контролеру; P (В2) =0,4 -вероятность того, что деталь попадет ко второму контролеру; PВ1 (A)=0,94 -вероятность того, что годная деталь будет признана первым контролером стандартной);
РB2 (A) = 0,98 - вероятность того, что годная деталь будет признана вторым контролером стандартной), Искомая вероятность PB1 (A)) = (0,6 • 0,94)/(0,б • 0,94 + 0,4-0,98) =0,59.
Задания 4-10. 1. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым -0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень. Ответ. 0,88. 2. У сборщика имеется 16 деталей, изготовленных заводом № 1, н 4 детали завода №2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется наготовленной заводом № 1. Ответ. 92/95. 3. В группе спортсменов 20 лыжников, б велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника - 0,9, для велосипедиста - 03 и для бегума - 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму. Ответ. 0,86. 4. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, н 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2-0,9, Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь. Ответ. 0,84. 5. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором-30 деталей, из них 24 стандартных; в третьем - 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика стандартная. Ответ. 43/60. 6. В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы. Ответ. 0,875. 7. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Иэ первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной. Ответ. 13/132. 8. Из полного набора' 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую извлеченную наудачу кость можно приставить к первой. Ответ. 7/18.
9. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей: когда он берет билет первым или последним? Ответ. Вероятности одинаковы в обоих случаях. 10. В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике. Ответ. 0,625. 11. При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-И срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором СИ или С-11, соответственно равны 0,6 н 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-Ш. Ответ. Вероятность того, что автомат снабжен сигнализатором С-1, равна 6/11. а С-11-5/11. 12. Для участия в спортивных студенческих отборочных соревнованиях выделено из первой группы курса 4, из второй - 6, из третьей группы - 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент? Ответ. Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59. Повторение испытаний. Формула Бернулли Рассмотрим практические ситуации. 1. Садовник покупает саженцы в магазине, где продавец сообщил ему, что вероятность проживания деревьев равна 90%. Сколько нужно купит садовнику саженцев, чтобы быть уверенным, что приживутся у него не менее 10 саженцев; ровно 10 саженцев; 2. Спортсмен бросает мяч по кольцу. Вероятность попадания в кольцо у него составляет 60%. Какова вероятность того, что при 15 бросках он попадет в кольцо равно 10 раз. Сформулируем общую таковую ситуацию. Вероятность наступления одного события равна p. Необходимо вычислить вероятность наступления k таких событий при n испытаниях Материал данного раздела позволит ответить на такие задания и решить много других ситуаций иного направления, связанных с повторными испытаниями.
Испытания называют независимыми относительно события А, е Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний. В независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность. Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность не наступления события А в каждом испытании также постоянна и равна q=1 - p. Рассмотрим задачу: Вычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз. и, следовательно, не осуществится п - k раз
Очевидно, что событие А повторилось ровно k раз в произвольной последовательности. Это значит, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: АААĀ, ААĀА, АĀАА, ĀААА, где.символ А обозначает, что событие наступила, а символ Ā – не наступило. Искомую вероятность обозначают Рп (k) или Pn,k, которая соответствует вероятности наступления события ровно k при n испытаниях. Такие задачи решаются по формуле Бернулли:
p - вероятность наступления события, q - вероятность не наступления события (q =1-p) Задание 4-11 1. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы. Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р=0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q=1- 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна: P6(4)=C64·0,754·0,252=0,30. 2. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,8 и не зависит от номера выстрела. Требуется найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень. Решение. п = 5, р = 0,8 и k = 2; по формуле Бернулли: Р5(2) =0,0512. 3. [3, №231]. Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз? 4. [3,№232]. По данным технического контроля 2% изготовленных автоматических станков нуждаются в дополнительной регулировке. Найдите вероятность того, что из 6 изготовленных станков 4 нуждаются в дополнительной регулировке. 5. [3, №240]. Вероятность того, что покупателю потребуется обувь 41-го размера, равна 0,2. Найдите вероятность того, что из 5 первых покупателей обувь этого размера понадобится: а) одному; б) по крайней мере, одному.
Локальная теорема Лапласа Выше была выведена формула Бернулли, позволяющая вычислить вероятность того, что событие появится в п испытаниях ровно k раз. При выводе мы предполагали, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях л достаточно трудно, так как формула требует выполнения действий над громадными числами. Правда, можно несколько упростить вычисления, пользуясь специальными таблицами логарифмов факториалов. Однако и этот путь остается громоздким и к тому же имеет существенный недостаток: таблицы содержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности; в итоге окончательный результат может значительно отличаться от истинного.
Локальная теорема Лапласа позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико. Теорема. Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции
Для удобства вычислений составлены таблицы значений функции Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна Pn(k)≈ Задание 4-12 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Решение. По условию, n = 400; k = 80; р=0,2; q= 0,8. Воспользуемся асимптотической формулой Лапласа: P400(80) = 0,04986. . 2. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз. Решение. По условию, п = 10; k = 8; р = 0,75; q = 0,25. Воспользуемся асимптотической формулой Лапласа: P10 (8)= 0,273.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.170 (0.028 с.) |
 , где n - число исходов, k – число положительных исходов,
, где n - число исходов, k – число положительных исходов, , причем,
, причем, 
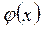 =
=  , соответствующие положительным значениям аргумента x. Функция
, соответствующие положительным значениям аргумента x. Функция  четная.
четная.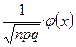 , где
, где