
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элемент «Исключающее ИЛИ» (XOR)
Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый. Эквивалентная схема примерно такая:
Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4. Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем. Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.
58. Интегральные оценки качества САР: Интегральные оценки дают обобщенную оценку быстроты затухания и величины отклонения регулируемой координаты, в виде единого числового значения. Находят применение первые три ИТ-оценки из перечисленных в списке: 1. I 1 и I 2 – линейные ИТ-оценки (не чувствительны к высшим производным координат САР). 2. I и I ′ – квадратичные ИТ-оценки (первая не чувствительна к высшим производным координат САР; вторая – к неподвижному режиму). 3. I + T 12 I ′ – улучшенная квадратичная ИТ-оценка (чувствительна к постоянной и к скоростной составляющим в движении координат САР). 4. I + T 12 I ′+ T 24 I ″+… – ИТ-оценки более высоких порядков (чувствительны к постоянной составляющей в движении координат САР, к их скорости, к ускорению,...).
Очевидно, что чем меньше значение оценки I 1 или I 2, тем лучше переходный процесс, но: a. Оценка I 1 не может применяться к колебательному переходному процессу. b. Аналитическое вычисление оценки I 2 по коэффициентам уравнения ошибки затруднено. c. Одно значение оценки I 2 может соответствовать переходным процессам с разной колебательностью (если совпадают мажоранты и миноранты).
Заметим, что оценку I ′ можно получить нахождением оценки I, если подать на вход САР не ступенчатую 1(t), а дельта функцию δ(t)=1′(t). Применение оценки I ′ ограничено тем, что она не чувствительна к установившемуся значению ошибки x ∞.
Очевидно, что I + T 12 I ′ будет минимальна при T 1 x ′+ x =(T 1 p +1) x =0. Решение этого ДУ есть экспонента: x (t)= x 0 e − t / T 1, а y (t)=1− x (t)= y 0(1− e − t / T 1). Т.е. улучшенная квадратичная ИТ-оценка I + T 12 I ′ будет иметь минимум при приближении переходной функции к экспоненте с заданной постоянной времени T 1.
Здесь оценка будет иметь минимум, только при перемещениях координат САР с определенными скоростью и ускорением, которые задаются постоянными времени T 1 и T 2 соответственно. Идея другого способа выбора параметров оценки заключена в том, что коэффициенты ДУ второго порядка можно выразить в виде затухания ζ и резонансной частоты q, которыми должна обладать настраиваемая САР.
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.168 (0.004 с.) |
 Он вот такой:
Он вот такой: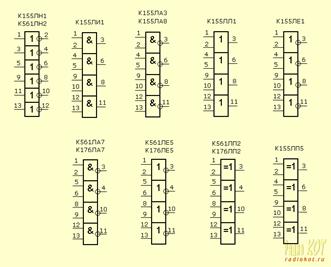 Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры. Ее запоминать не обязательно.
Ее запоминать не обязательно. Пусть имеем переходные функции h (t).
Пусть имеем переходные функции h (t). Рассмотрим линейные ИТ-оценки:
Рассмотрим линейные ИТ-оценки: .
. Ограничения "a" и "b" для оценок I 1 и I 2 преодолеваются квадратичными ИТ-оценками I и I ′:
Ограничения "a" и "b" для оценок I 1 и I 2 преодолеваются квадратичными ИТ-оценками I и I ′: .
. Ограничение "c" и другие ограничения оценок I 1, I 2, I и I ′ снимаются улучшенной квадратичной ИТ-оценкой:
Ограничение "c" и другие ограничения оценок I 1, I 2, I и I ′ снимаются улучшенной квадратичной ИТ-оценкой: , где: x 0 – начальное значение отклонения в переходном процессе; I + T 12 I ′ – не формула, а составной символ обозначения данной ИТ-оценки.
, где: x 0 – начальное значение отклонения в переходном процессе; I + T 12 I ′ – не формула, а составной символ обозначения данной ИТ-оценки. Можно использовать улучшенные ИТ-оценки более высоких порядков. Например:
Можно использовать улучшенные ИТ-оценки более высоких порядков. Например: .
.


