Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскости частного положения. Особенности их проекций
Плоскость, перпендикулярная одной плоскости проекций.
Любой элемент, лежащий в этой плоскости, проецируется на плоскость П 1 в прямую Г 1, называемую горизонтальным следом плоскости. Угол наклона горизонтально проецирующей плоскости к плоскости проекций П 2 на комплексном чертеже определяется как угол 1, заключенный между горизонтальным следом Г 1 данной плоскости и прямой, перпендикулярной линиям связи (рис.3.7-б).
Фронтально проецирующей плоскостью (рис.3.8) называют плоскость, перпендикулярную к плоскости проекций П 2. Любой элемент этой плоскости проецируется на фронтальную плоскость проекций в прямую Ф 2 - фронтальный след плоскости. Угол наклона фронтально проецирующей плоскости к плоскости П 1 на комплексном чертеже определяется как угол 2, заключенный между фронтальным следом Ф 2 и прямой, перпендикулярной линиям связи. Профильно проецирующей плоскостью называют плоскость, перпендикулярную к профильной плоскости проекций (рис.3.9). Любой элемент, лежащий в этой плоскости, проецируется на профильную плоскость проекций в прямую 3 - профильный след плоскости. На профильной проекции углы и наклона профильно проецирующей плоскости к плоскостям П 2 и П 2изображаются без искажения.
Плоскости частного положения, перпендикулярные двум плоскостям проекций и параллельные третьей плоскости проекций, называются плоскостями уровня: фронтальная плоскость уровня параллельна плоскости проекций V и перпендикулярна плоскостям Н и W.Её признаки: её горизонтальная и профильная проекции представляют собой прямые, параллельные осям Х и Z. Горизонтальная плоскость уровня параллельна плоскости проекций Н и перпендикулярна плоскостям V и W; Признаки: ее фронтальная и профильная проекции проецируются в прямые, параллельные осям Х и У. Профильная плоскость уровня параллельна плоскости проекций W и перпендикулярна плоскостям V и Н; Признаки: ее фронтальная и горизонтальная проекции представляют собой прямые, перпендикулярные оси Х.
Образование поверхности. Определитель поверхности. Каркас поверхности. Поверхность - совокупность всех последовательных положений перемещающейся в пространстве линии по определенному закону. Этот подход предполагает формирование поверхности в результате перемещения одной кривой U (образующей) по другой кривой V (направляющей) в соответствии с рисунком 1.
а) Ф (а, m) [ А1 ] б) Ф (с, m) [ А2 ] в) Ф (р, m) [ А3 ]
Образование поверхности вращения. Очерк поверхности. Рис. 3.15
Рис. 3.16
Рис 3.17
Сферическая поверхность образуется за счет вращения окружности вокруг оси, проходящей через центр окружности и лежащей в ее плоскости (рис.3.18). Экватор и меридианы сферической поверхности являются равными между собой окружностями. Поэтому при ортогональном проецировании на любую плоскость сферическая поверхность проецируется в круги.
11.ПОЗИЦИОННЫЕ ЗАДАЧИ.ПРИНАДЛЕЖНОСТЬ ТОЧКИ, ЛИНИИ ПОВЕРХНОСТИ.ТЕОРЕМА МОНЖА. Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности). К позиционным относятся также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам. Первая группа задач может быть объединена под общим названием задачи на принадлежность. К ним, в частности, относятся задачи на определение:1) принадлежности точки линии;2) принадлежности точки поверхности;3) принадлежности линии поверхности.Ко второй группе относятся задачи на пересечение. Эта группа содержит также три типа задач:1) на пересечение линии с линией;2) на пересечение поверхности с поверхностью;3) на пересечение линии с поверхностью. Принадлежность точки поверхности. Основное положение при решении задач для этого варианта принадлежности следующее: точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. В этом случае линии надо выбирать наиболее простыми, чтобы легче было построить проекции такой линии, затем использовать то обстоятельство, что проекции точки, лежащие на поверхности, должны принадлежать одноименным проекциям линии этой поверхности. Пример решение этой задачи показан на рисунке. Здесь есть два пути решения, поскольку можно провести две простейших линии, принадлежащих конической поверхности. В первом случае — проводится прямая линия - образующая конической поверхности S1 так, чтобы она проходила через какую-либо заданную проекцию точки С. Тем самым предполагаем, что точка С принадлежит образующей S1 конической поверхности, а следовательно - самой конической поверхности. В этом случае одноименные проекции точки С должны лежать на соответствующих проекциях этой образующей.Другая простейшая линия - окружность с диаметром 1-2 (радиус этой окружности - отсчитывается от оси конуса до очерковой образующей). Этот факт известен еще из школьного курса геометрии: при пересечении кругового конуса плоскостью, параллельной его основанию, или перпендикулярной к его оси, в сечении будет получаться окружность. Второй способ решения позволяет найти недостающую проекцию точки С, заданной своей фронтальной проекцией, принадлежащей поверхности конуса и совпадающей на чертеже с осью вращения конуса, без построения третьей проекции. Всегда следует иметь в виду, видима или не видима точка, лежащая на поверхности конуса (в случае, если она не видна, соответствующая проекция точки будет заключена в скобки). Очевидно, что в нашей задаче точка С принадлежит поверхности, поскольку проекции точки принадлежат одноимённым проекциям линий, использованных для решения как при первом, так и при втором способе решения. Принадлежность линии поверхности. Основное положение: линия принадлежит поверхности, если все точки линии принадлежат заданной поверхности. Это означает, что в данном случае принадлежности должна быть несколько раз решена задача о принадлежности точки поверхности. Торема Монжа:если две поверхности второго порядка описаны около третьей или вписаны в неё, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения окружности касания.
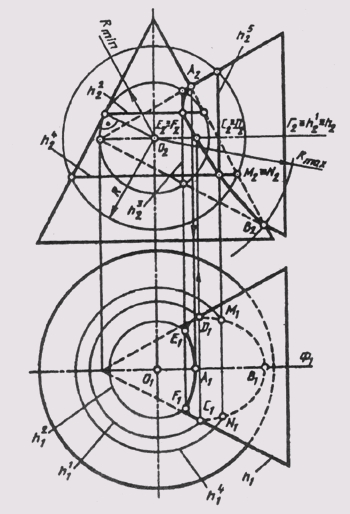
№13.Соосные поверхности. Метод концентрических сфер. При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, соосные с данными поверхностями. К соосным поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены соосные цилиндр и сфера (рис. 134, а), соосные конус и сфера (рис. 134, б) и соосные цилиндр и конус (рис. 134, в) .Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 1 и 2 пересечения их главных меридианов. Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения. Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер. При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:1) пересечение поверхностей вращения;2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях. Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф1) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П2 или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h', лежащих в одной вспомогательной секущей плоскости Г(Г2), определены точки видимости С и D линии пересечения относительно плоскости П1. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О1; О2), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах Rmin < R < Rmах- Радиус максимальной сферы определяется расстоянием от центра О наиболее удаленной точки В (Rmax = О2В2), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (по окружности h2) и пересекающей другую (по окружности h3).Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей: h22 ^ h32 = E2(F2); Е2Е1 || А2А1; Е2Е1 ^ h21 =E1; F2F ^ h1 = F1 Промежуточная сфера радиуса R пересекает поверхности по окружностям h4 и h5, в пересечении которых находятся точки Ми N:h42 ^ h52 = M2(N2); M2M1 || А2А1, М2М1 ^ h41 = М1; N2N1 ^ h41 = N1 Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.
№14. построение линии пересечения поверхностей, если хотя бы одна из них проецирующая. Характерные точки линии пересечения. Прежде чем приступить к построению линии пересечения поверхностей, необходимо внимательно изучить условие задачи, т.е. какие поверхности пересекаются. Если одна из поверхностей является проецирующей, то решение задачи упрощается, т.к. на одной из проекций линия пересечения совпадает с проекцией поверхности. И задача сводится к нахождению второй проецирующей линии. При решении задачи следует отметить в первую очередь «характерные» точки или «особые». Это: · Точки на крайних образующих · Точки, делящие линию на видимую и невидимую часть · Верхние и нижние точки и др. Далее следует разумно выбрать способ, каким будем пользоваться при построении линии пересечения поверхностей. Мы будем пользоваться двумя способами: 1. вспомогательных секущих плоскостей. 2. вспомогательных секущих сфер. К проецирующим поверхностям относятся: 1) цилиндр, если его ось перпендикулярна плоскости проекций; 2) призма, если ребра призмы перпендикулярны плоскости проекций. Проецирующая поверхность проецируется в линию на плоскость проекций. Все точки и линии, принадлежащие боковой поверхности проецирующего цилиндра или проецирующей призме проецируются в линию на ту плоскость, которой ось цилиндра или ребро призмы перпендикулярно. Линия пересечения поверхностей принадлежит обеим поверхностям одновременно и, если одна из этих поверхностей проецирующая, то для построения линии пересечения можно использовать следующее правило: если одна из пересекающихся поверхностей проецирующая, то одна проекция линии пересечения есть на чертеже в готовом виде и совпадает с проекцией проецирующей поверхности (окружность, в которую проецируется цилиндр или многоугольник, в который проецируется призма). Вторая проекция линии пересечения строится исходя из условия принадлежности точек этой линии другой не проецирующей поверхности. Рассмотренные особенности характерных точек позволяют легко проверить правильность построения линии пересечения поверхностей, если она построена по произвольно выбранным точкам. В данном случае десяти точек достаточно для проведения плавных проекций линии пересечения. При необходимости может быть построено любое количество промежуточных точек. Построенные точки соединяют плавной линией с учетом особенностей их положения и видимости. Сформулируем общее правило построения линии пересечения поверхностей: выбирают вид вспомогательных поверхностей; строят линии пересечения вспомогательных поверхностей с заданными поверхностями; находят точки пересечения построенных линий и соединяют их между собой. Вспомогательные секущие плоскости выбираем таким образом, чтобы в пересечении с заданными поверхностями получались геометрически простые линии (прямые или окружности). Выбираем вспомогательные секущие плоскости. Чаще всего, в качестве вспомогательных секущих плоскостей выбирают проецирующие плоскости, в частности, плоскости уровня. При этом необходимо учитывать линии пересечения, получаемые на поверхности, в результате пресечения поверхности плоскостью. Так конус является наиболее сложной поверхностью по числу получаемых на нем линий. Только плоскости, проходящие через вершину конуса или перпендикулярные оси конуса, пересекают его соответственно по прямой линии и окружности (геометрически простейшие линии). Плоскость, проходящая параллельно одной образующей пересекает его по параболе, плоскость параллельная оси конуса пересекает его по гиперболе, а плоскость, пересекающая все образующие и наклонные к оси конуса, пересекает его по эллипсу. На сфере, при пересечении ее плоскостью, всегда получается окружность, а если пересекать ее плоскостью уровня, то эта окружность проецируется на плоскости проекции соответственно в прямую линию и окружность. Итак, в качестве вспомогательных плоскостей выбираем горизонтальные плоскости уровня, которые пересекают и конус, и сферу по окружностям (простейшие линии). Некоторые особые случаи пересечения поверхностей В некоторых случаях расположение, форма или соотношения размеров криволинейных поверхностей таковы, что для изображения линии их пресечения никаких сложных построений не требуется. К ним относятся пересечение цилиндров с параллельными образующими, конусов с общей вершиной, соосных поверхностей вращения, поверхностей вращения, описанных вокруг одной сферы.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.184.214 (0.023 с.) |
 Рис. 3.7-а
Рис. 3.7-а  Рис. 3.7-б
Рис. 3.7-б Рис. 3.8-а
Рис. 3.8-а  Рис. 3.8-б
Рис. 3.8-б Рис. 3.9.
Рис. 3.9. Поверхности вращения имеют весьма широкое применение во всех областях техники. Поверхностью вращения называют поверхность, получающуюся от вращения некоторой образующей линии 1 вокруг неподвижной прямой i - оси вращения поверхности (рис.3.15). На чертеже поверхность вращения задается своим очерком. Очерком поверхности называются линии, которые ограничивают области ее проекций. При вращении каждая точка образующей описывает окружность, плоскость которой перпендикулярна оси. Соответственно, линия пересечения поверхности вращения плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями (рис. 3.15). Параллель наибольшего радиуса называют экватором, наименьшего - горлом. Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхностью вращения - меридианом. Меридиан, лежащий в плоскости, параллельной плоскости проекций, называют главным меридианом. В практике выполнения чертежей наиболее часто встречаются следующие поверхности вращения: цилиндрическая, коническая, сферическая, торовая.
Поверхности вращения имеют весьма широкое применение во всех областях техники. Поверхностью вращения называют поверхность, получающуюся от вращения некоторой образующей линии 1 вокруг неподвижной прямой i - оси вращения поверхности (рис.3.15). На чертеже поверхность вращения задается своим очерком. Очерком поверхности называются линии, которые ограничивают области ее проекций. При вращении каждая точка образующей описывает окружность, плоскость которой перпендикулярна оси. Соответственно, линия пересечения поверхности вращения плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями (рис. 3.15). Параллель наибольшего радиуса называют экватором, наименьшего - горлом. Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхностью вращения - меридианом. Меридиан, лежащий в плоскости, параллельной плоскости проекций, называют главным меридианом. В практике выполнения чертежей наиболее часто встречаются следующие поверхности вращения: цилиндрическая, коническая, сферическая, торовая. Цилиндрическую поверхность вращения. В качестве направляющей а следует взять окружность, а в качестве прямой b - ось i (рис.3.16). Тогда получим, что образующая l, параллельная оси i, вращается вокруг последней. Если ось вращения перпендикулярна горизонтальной плоскости проекций, то на П 1 цилиндрическая поверхность проецируется в окружность, а на П 3 - в прямоугольник. Главным меридианом цилиндрической поверхности являются две параллельные прямые.
Цилиндрическую поверхность вращения. В качестве направляющей а следует взять окружность, а в качестве прямой b - ось i (рис.3.16). Тогда получим, что образующая l, параллельная оси i, вращается вокруг последней. Если ось вращения перпендикулярна горизонтальной плоскости проекций, то на П 1 цилиндрическая поверхность проецируется в окружность, а на П 3 - в прямоугольник. Главным меридианом цилиндрической поверхности являются две параллельные прямые.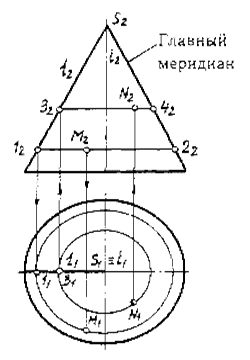 Коническую поверхность вращения получим, вращая прямолинейную образующую l вокруг оси i. При этом образующая l пересекает ось i в точке S, называемой вершиной конуса (рис.3.17). Главным меридианом конической поверхности являются две пересекающиеся прямые. Если в качестве образующей взять отрезок прямой, а ось конуса перпендикулярной П 1, то на П 1коническая поверхность проецируется в круг, а на П 2 - в треугольник.
Коническую поверхность вращения получим, вращая прямолинейную образующую l вокруг оси i. При этом образующая l пересекает ось i в точке S, называемой вершиной конуса (рис.3.17). Главным меридианом конической поверхности являются две пересекающиеся прямые. Если в качестве образующей взять отрезок прямой, а ось конуса перпендикулярной П 1, то на П 1коническая поверхность проецируется в круг, а на П 2 - в треугольник. Рис. 3.18 При вращении окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, образуется поверхность, называемая торовой (рис.3.19).
Рис. 3.18 При вращении окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, образуется поверхность, называемая торовой (рис.3.19). Рис. 3.19
Рис. 3.19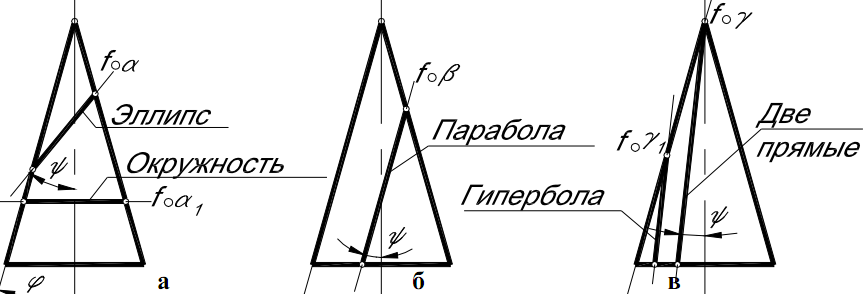
 12.СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ. При пересечении поверхностей тел проецирующими плоскостями, одна проекция сечения совпадает с проекцией проецирующей плоскости. Конус может иметь в сечении пять различных фигур. Треугольник - если секущая плоскость пересекает конус через вершину по двум образующим. Окружность - если плоскость пересекает конус параллельно основанию (перпендикулярно оси). Эллипс - если плоскость пересекает все образующие под некоторым углом. Параболу - если плоскость параллельна одной из образующих конуса. Гиперболу - если плоскость параллельна оси или двум образующим конуса. Сечение поверхности плоскостью представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности. При пересечении плоскостью многогранника в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника. Пример. Построить проекции линии пересечения L поверхности прямого кругового конуса ω плоскостью β. Решение. В сечении получается парабола, вершина которой спроецируется в точку А (А′, А′′). Точки A, D, E линии пересечения являются экстремальными. На рис. построение искомой линии пересечения осуществлено с помощью горизонтальных плоскостей уровня αi, которые пересекают поверхность конуса ω по параллелям рi, а плоскость β - по отрезкам фронтально проецирующих прямых. Линия пересечения L полностью видима на плоскостях.
12.СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ. При пересечении поверхностей тел проецирующими плоскостями, одна проекция сечения совпадает с проекцией проецирующей плоскости. Конус может иметь в сечении пять различных фигур. Треугольник - если секущая плоскость пересекает конус через вершину по двум образующим. Окружность - если плоскость пересекает конус параллельно основанию (перпендикулярно оси). Эллипс - если плоскость пересекает все образующие под некоторым углом. Параболу - если плоскость параллельна одной из образующих конуса. Гиперболу - если плоскость параллельна оси или двум образующим конуса. Сечение поверхности плоскостью представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности. При пересечении плоскостью многогранника в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника. Пример. Построить проекции линии пересечения L поверхности прямого кругового конуса ω плоскостью β. Решение. В сечении получается парабола, вершина которой спроецируется в точку А (А′, А′′). Точки A, D, E линии пересечения являются экстремальными. На рис. построение искомой линии пересечения осуществлено с помощью горизонтальных плоскостей уровня αi, которые пересекают поверхность конуса ω по параллелям рi, а плоскость β - по отрезкам фронтально проецирующих прямых. Линия пересечения L полностью видима на плоскостях.