
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопередача при наличии внутренних источников теплоты
В ряде случаев в середине стенки могут происходить процессы, в результате которых выделяется или поглощается тепло. Примерами таких процессов могут быть: выделение джоулевой теплоты при прохождении электрического тока по проводникам, объемное выделение теплоты в результате протекания экзотермической реакции или поглощения теплоты при протекании эндотермической реакции и т.д. При исследовании переноса теплоты в таких случаях важно знать интенсивность объемного выделения (поглощения) теплоты, которая количественно определяется мощностью внутреннего источника (стока) теплоты qn. В частном случае, когда выделяется джоулево тепло при прохождении электрического тока через проводник цилиндрической формы, мощность внутреннего источника тепла может быть определена из уравнения:
где Q – количество теплоты; d – диаметр проводника, l – длина проводника. Количество теплоты, выделяющейся при прохождении электрического тока по проводнику (джоулево тепло), определяется через параметры электрического тока: силу тока (I), напряжение (U), электрическое сопротивление
Теплопроводность плоской стенки (плоский ТВЭЛ)
Для стационарного процесса (¶t/¶t=0) одномерного распространения теплоты в плоской стенке (m=0) при наличии внутреннего источника теплоты (qn) дифференциальное уравнение теплопроводности
принимает вид
С учетом того, что
Имеем уравнения второго порядка. Для его решения необходимо снизить порядок, введя новую функцию
После разделения переменных и интегрирования имеем:
После разделения переменных и интегрирования имеем:
После интегрирования окончательно получим:
Постоянные интегрирования С 1 и С 2 определяются из граничных условий. Последнее уравнение описывает в общем виде распределение температуры в плоской стенке при наличии внутренних источников тепла. Из общего решения можно получить уравнения для конкретных задач.
Теплопроводность пластины при одинаковой температуре ее поверхностей
Дана плоская стенка толщиной 2d. В стенке действует постоянный по объему внутренний источник тепла мощностью qv. На поверхностях стенки поддерживается постоянная температура t ст (симметричная задача). Необходимо определить распределение температуры в стенке и количество теплоты, отдаваемое стенкой в окружающую среду.
Поместим начало координат в центре стены. Тогда координаты правой и левой граней стенки будут равны соответственно + d и - d. Исходя из условий задачи, можно составить граничные условия: при при
Второе граничное условие называется условием тепловой симметрии. Действительно, при одинаковой температуре поверхностей стенки тепловые потоки через правую и левую грани должны быть одинаковые, но противоположно направлены. Поэтому в центре стенки тепловой поток будет равен нулю, то есть:
Но l¹0, следовательно Используя граничные условия, можно определить постоянные интегрирования С 1 и С 2 в уравнении Поскольку Из второго граничного условия
откуда
Подставляя значения С 1 и С 2 в уравнение, получим:
Имеем параболическое распределение температуры в стенке (см. Рис.). Нетрудно определить максимальную температуру (t max) в стенке. Очевидно, что максимальная температура в стенке (t max) будет иметь место при х = 0. Тогда:
Для определения количества тепла, отводимого через левую и правую грани стенки, воспользуемся уравнением Фурье:
Количество тепла, отводимого через правую грань стенки при (х=+d), равно:
Аналогично можно определить количество тепла, выделяемого через левую грань (х= -d), то есть:
Согласно
Тогда имеем:
Общее количество тепла, выделяемого стенкой толщиной 2 d, равно: q=|qлев|+|qпр|=2d . qn.
Однородный цилиндр (ТВЭЛ)
Условия теплоотдачи со всех сторон одинаковы (симметричная задача), то есть можно рассматривать только правую половину цилиндра. Дифференциальное уравнение теплопроводности для стационарного режима имеет вид
получим дифференциальное уравнение теплопроводности для цилиндра при стационарном режиме:
Граничные условия:
это уравнение параболы.
Температура на оси цилиндра находится при r = 0:
Температура стенке цилиндра находится при r = r 0:
Удельный тепловой поток, Вт/м² находится из последнего соотношения и теплота, отданная от цилиндра к окружающей его жидкости, Вт
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.48.131 (0.011 с.) |
 ,
, :
: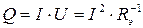 .
.
 .
. , последнее уравнение можно записать в другом виде:
, последнее уравнение можно записать в другом виде: .
. . Тогда данное уравнение примет вид:
. Тогда данное уравнение примет вид: .
. .
. .
.
 ,
, .
.

 .
. .
. , то С 1=0.
, то С 1=0. ,
, .
. .
. .
.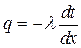 .
. .
.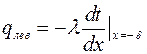 .
. при С 1=0
при С 1=0 .
. ;
; .
. Для бесконечного цилиндрического стержня
Для бесконечного цилиндрического стержня  , при стационарном режиме
, при стационарном режиме

 где оператор Лапласа в полярных координатах
где оператор Лапласа в полярных координатах В бесконечном цилиндре температура изменяется только по радиусу, то есть:
В бесконечном цилиндре температура изменяется только по радиусу, то есть: после деления на коэффициент температуропроводности
после деления на коэффициент температуропроводности

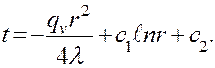 После двойного интегрирования имеем
После двойного интегрирования имеем Определив константы интегрирования и подставив их в последнее уравнение, имеем:
Определив константы интегрирования и подставив их в последнее уравнение, имеем:







