
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление средней арифметической
В общем виде расчет проводится по формуле:
где
Контрольный пример
Вычисление взвешенной средней арифметической Для случая, если показатели повторяются, и они сгруппированы т.е. результаты измерений представлены в виде вариационного ряда – ранжированного ряда вариант с указанием их частоты. В общем виде расчет проводится по формуле:
где
Вычисление взвешенной средней арифметической по средним величинам Тогда формула приобретает вид:
где
Контрольный пример
Оценку точности полученной средней величины производят с помощью производного показателя отношения стандартной ошибки среднего значения m к среднему значению
Этот показатель в определенной мере может характеризовать репрезентативность (представительность) исследуемой выборки. Если показатель Тс будет менее 5%, то можно с достаточной уверенностью утверждать, что полученная выборка хорошо отражает центральную тенденцию генеральной совокупности, из которой эта выборка взята. Если прирост результатов в спортивной тренировке оценивают по отношению к некоторому уровню в процентах, в этом случае вычисляется средняя геометрическая по формуле:
где П – знак произведения Контрольный пример: Прирост результатов за три периода тренировки составил 40%, 25% и 8%.
Однако вычисление средних величин еще не полностью характеризует изучаемую группу испытуемых. Предположим, что были получены одинаковые средние результаты в подтягивании – 10 раз. в двух группах испытуемых. Однако в первой группе результаты колебались в пределах от 7 до 18, а в другой с 12 до 18. Естественно предположить, что вторая группа более однородна по своей подготовке, а в первой группе имеется значительное число лиц слабо подготовленных в этом упражнении. Средние результаты в данном случае маскируют качество проведенной работы, не показывают разнообразия результатов, которое присуще анализируемой совокупности. То есть, часть информации о совокупности теряется.
Кроме средних величин, для полной характеристики совокупности, необходимо использовать и показатели разнообразия полученных результатов. Наиболее полную характеристику степени разнообразия (или вариативности) можно получить при помощи среднеквадратического отклонения. В общем виде расчет проводится по формуле:
исходя из этой формулы, для вычисления среднего квадратичного отклонения необходимо последовательно провести следующие вычисления: а) найти среднюю квадратичную б) вычислить отклонение каждой варианты от средней арифметической и затем возвести все эти отклонения в квадрат - в) суммировать все квадраты отклонений от средней арифметической - г) разделить полученную сумму на число вариант без одной и извлеч квадратный корень - При распределении близком к нормальному в интервале + 0,67 Контрольный пример:
Для быстрого, но приближенного вычисления сигмы можно использовать формулу С. И. Ермолаева и Р. Н. Бирюковой (1962):
где
к – табличный коэффициент, соответствующий определенному числу вариант. Например при: N = 10 – 20 –30 – 40 –50 – 60 – 70 – 80 – 90 - 100 к = 3,08 – 3,74 –4,09 –4,30 – 4,50 – 4,64 - 4,76 – 4,85 – 4,94 – 5,02.
В практике исследований по физической подготовке широкое распространение получило выражение экспериментальных данных в 9 – балльной шкале оценок, которая может быть основана на показателях стандартного отклонения.
Таблица 39
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.130.13 (0.006 с.) |
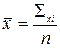 ,
,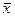 - средняя арифметическая величина;
- средняя арифметическая величина;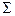 - знак суммирования;
- знак суммирования;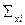 - сумма всех показателей;
- сумма всех показателей;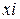 - варианта (отдельное значение изучаемого признака);
- варианта (отдельное значение изучаемого признака); - количество этих показателей (вариант).
- количество этих показателей (вариант).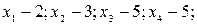
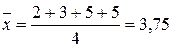
 ,
,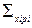 - сумма произведений каждой величины (варианты) xi на их количество pi;
- сумма произведений каждой величины (варианты) xi на их количество pi;
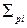 - общее количество вариант.
- общее количество вариант. небольших рядов, содержащих разное количество вариант
небольших рядов, содержащих разное количество вариант 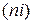 .
. ,
, - сумма произведений каждой средней величины на количество вариант из которых она выведена;
- сумма произведений каждой средней величины на количество вариант из которых она выведена;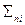 - общее количество всех вариант.
- общее количество всех вариант.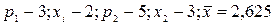
 , который вычисляется по формуле:
, который вычисляется по формуле: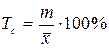
 ,
,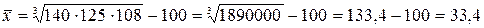
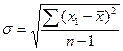
 по уже известной нам формуле;
по уже известной нам формуле; ;
;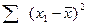
 .
.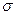 от среднего значения, как правило располагается 50% возможных значений признака, в интервале
от среднего значения, как правило располагается 50% возможных значений признака, в интервале  располагается 68,3% вариаций, а в интервале
располагается 68,3% вариаций, а в интервале 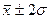 располагается 95,% и в интервале
располагается 95,% и в интервале 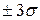 - 99,7% вариант. Минимальное и максимальное значения признака не удаляется от среднего значения больше, чем на три
- 99,7% вариант. Минимальное и максимальное значения признака не удаляется от среднего значения больше, чем на три 
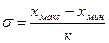 ,
, - наибольшее значение варианты
- наибольшее значение варианты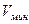 - наименьшее значение варианты
- наименьшее значение варианты


