Комплексная плоскость. Арифметические действия над комплексными числами

Ко́мпле́ксная плоскость ^[1] — это двумерное вещественное пространство , которое изоморфно полю комплексных чисел . Каждая точка такого пространства — этоупорядоченная пара вида 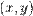, где и — вещественные числа, и где первый элемент пары соответствует вещественной части, а второй элемент пары соответствует мнимой части комплексного числа :

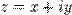Упорядоченную пару естественно интерпретировать как радиус-вектор с началом в нуле и с концом в точке . В силу изоморфизма между и , алгебраические операции над комплексными числами переносятся на операции над соответствующими им радиус-векторами: сложение комплексных чисел — это сложение соответствующих радиус-векторов; умножение комплексных чисел — это преобразование радиус-вектора, связанное с его поворотом и растяжением. Результатом компактификации комплексной плоскости является расширенная комплексная плоскость — комплексная плоскость, дополненная бесконечно удалённой точкой, изоморфная комплексной сфере. Комплексная плоскость связана с комплексной сферой, например, стереографической проекцией. Комплекснозначные функции комплексного переменного обычно интерпретируются как отображения комплексных плоскости или сферы в себя. Поскольку прямые на плоскости (при стереографической проекции) переходят в окружности на сфере, содержащие бесконечно удалённую точку, комплексные функции удобнее рассматривать на сфере. Рассматривая на комплексной плоскости топологию , можно вводить понятия открытых, замкнутых множеств, и давать определения таким объектам как кривые и формулировать такие свойства комплексных функций как непрерывность, дифференцируемость и аналитичность, а комплексное представление позволяет компактно описывать эти свойства на языке соотношений между вещественными и мнимыми частями, а также, между модулями и аргументами соответствующих комплексных чисел. Особую роль в комплексном анализе играют конформные отображения.

Сумма Суммой комплексных чисел z1 = a + bi и z2 = с + di называется комплексное число (a + c) + (b + d)i. Таким образом: z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i. Сумма комплексных чисел обладает свойствами:  коммутативности: z1 + z2 = z2 + z1  ассоциативности: (z1 + z2) + z3 = z1 + (z2 + z3) Произведение Произведением комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число (ac - bd)+(ad + bc)i. Определение произведения устанавливается с таким расчетом, чтобы (a + bi) и (c + di) можно было перемножить как алгебраические двучлены, считая при этом, что i*i = -1. Произведение комплексных чисел обладает свойствами:  коммутативности: z1 * z2 = z2 * z1  ассоциативности: (z1 * z2) * z3 = z1 * (z2 * z3)  дистрибутивности: z1 * (z2 + z3) = z1 * z2 + z1 * z3 На основании определения произведения комплексных чисел можно определить натуральную степень комплексного числа: z(в степени n); = z * z *... * z n раз. Разность Разностью комплексных чисел z1 = a + bi и z2 = c + di называется комп­лек­сное число z = z1 - z2 = (a - c) + (b - d)i. ЧастноеЧастным от деления комплексного числа z1 на комплексное число z2 на­зывается такое число z, которое удовлетворяет условию z? z2 = z2? z= = z1.