
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Початкове рівняння напишемо в матричній формі
Матричне рівняння виду
Для даної матриці
и
Відповідь:
2) Зайти невідому матрицю
Розв’язання. Початкове рівняння напишемо в матричній формі
Матричне рівняння виду
Для даної матриці
Тоді
Відповідь:
Індивідуальні завдання
Варіант № 1
1.1.
1.4.
1.5.
Варіант № 2
2.1.
2.4.
2.5.
Варіант № 3
3.1
3.4.
3.5.
Варіант № 4
4. 1.
4.4.
4.5.
Варіант № 5
5.1.
5.4.
5.5.
Варіант № 6
6.1.
6.4.
6.5.
Варіант № 7
7.1.
7.4.
7.5.
Варіант № 8
8.1.
8.4.
8.5.
Варіант № 9
9.1.
9.4.
9.5.
Варіант № 10
10.1.
10.4.
10.5.
Варіант № 11
11.1.
11.4.
11.5.
Варіант № 12
12.1.
12.4.
12.5.
Варіант № 13
13.1.
13.4.
13.5.
Варіант № 14
14.1.
14.4.
14.5.
Варіант № 15
15.1.
15.4.
15.5.
Варіант № 16
16.1.
16.4.
16.5.
Варіант № 17
17.1.
17.4.
17.5.
Варіант № 18
18.1.
18.4.
18.5.
Варіант № 19
19.1.
19.4.
19.5.
Варіант № 20
20.1.
20.4.
20.5.
Варіант № 21
21.1.
21.4.
21.5.
Варіант № 22
22.1.
22.4.
22.5.
Варіант № 23
23.1.
23.4.
23.5.
Варіант № 24
24.1.
24.4.
24.5.
Варіант № 25
25.1.
25.4.
25.5.
Варіант № 26
26.1.
26.4.
26.5.
Варіант № 27
27.1.
27.4.
27.5.
Варіант № 28
28.1.
28.4.
28.5.
Варіант № 29
29.1.
29.4.
29.5.
Варіант № 30
30.1.
30.4.
30.5.
1.2 СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ Завдання 1.2 Методом Крамера знайти розв’язання системи лінійних алгебраїчних рівнянь. Встановити, що система рівнянь має єдиний розв’язок, і знайти його за допомогою оберненої матриці. Методом Гауса (або методом виключення невідомих) знайти розв’язання системи лінійних алгебраїчних рівнянь. Знайти загальний розв'язок однорідної системи лінійних алгебраїчних рівнянь. 5. При яких значеннях Зразок розв’язання. Методом Крамера знайти розв’язок системи лінійних алгебраїчних рівнянь.
Розв’язання. Розв’язок системи знаходимо за формулами Крамера
Обчислимо визначник системи
Послідовно замінивши в
Відповідь:
Задана система з трьох рівнянь з трьома невідомими. Встановити, що система рівнянь має єдиний розв’язок, і знайти його за допомогою оберненої матриці.
Розв’язання. Якщо визначник системи відмінний від нуля, то система має єдиний розв’язок (теорема Крамера). Обчислимо визначник даної системи:
отже, система має єдиний розв’язок. Дану систему можна записати у матричній формі:
Оскільки Знайдем обернену матрицю
де
Тоді
Відповідь:
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.166.7 (0.149 с.) |
 , де
, де  ,
,  .
.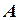 і
і 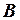 – квадратні матриці однакового порядку і матриця
– квадратні матриці однакового порядку і матриця  . У цьому випадку для матриці
. У цьому випадку для матриці 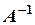 . Помноживши ліворуч обидві частини рівняння
. Помноживши ліворуч обидві частини рівняння  , де
, де  одинична матриця,
одинична матриця, шукана матриця.
шукана матриця. . Отже, існує
. Отже, існує  , де
, де  алгебраїчне доповнення елемента
алгебраїчне доповнення елемента  матриці
матриці  . Тогда
. Тогда 

 .
. .
.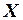 з рівняння
з рівняння .
. , де
, де  ,
,  .
. , тобто для матриці
, тобто для матриці  , де
, де  одинична матриця, або
одинична матриця, або  , або
, або шукана матриця.
шукана матриця. . Отже, існує
. Отже, існує  и
и .
.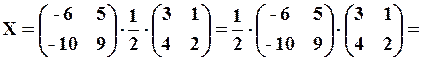
 .
. .
. 1.2.
1.2. 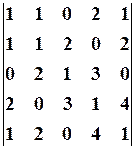 1.3.
1.3. 
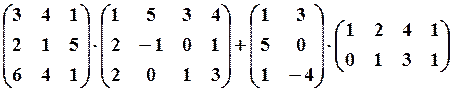
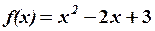 ,
,  1.6.
1.6. 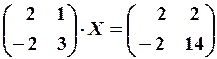
 2.2.
2.2. 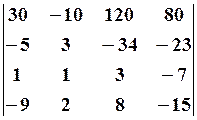 2.3.
2.3. 

 ,
, 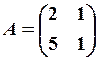 2.6.
2.6. 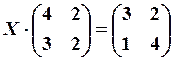
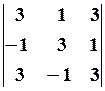 3.2.
3.2. 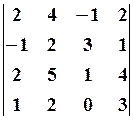 3.3.
3.3. 
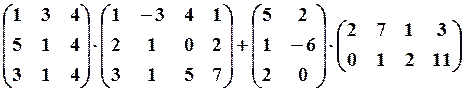
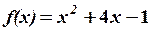 ,
, 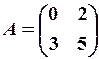 3.6.
3.6. 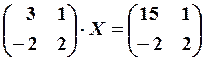
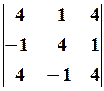 4.2.
4.2. 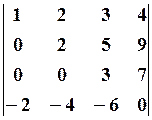 4.3.
4.3. 
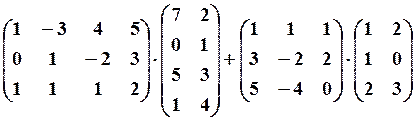
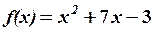 ,
,  4. 6.
4. 6. 
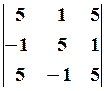 5.2.
5.2. 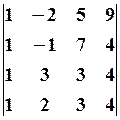 5.3.
5.3. 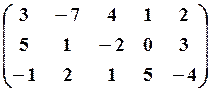
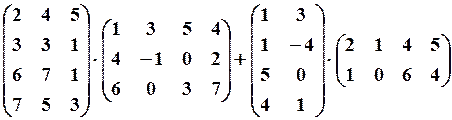
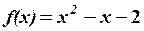 ,
, 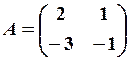 5.6.
5.6. 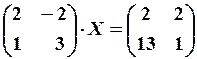
 6.2.
6.2. 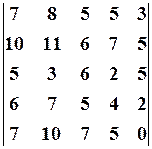 6.3.
6.3. 

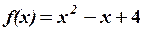 ,
, 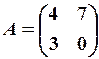 6.6.
6.6. 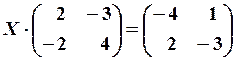
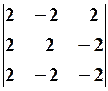 7.2.
7.2. 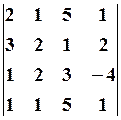 7.3.
7.3. 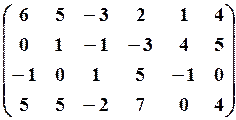
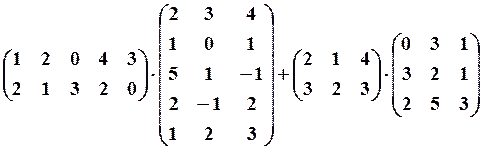
 ,
, 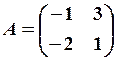 7. 6.
7. 6. 
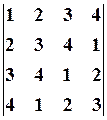 8.3.
8.3. 

 ,
, 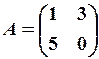 8.6.
8.6. 
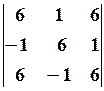 9.2.
9.2. 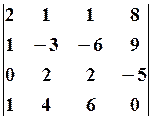 9.3.
9.3. 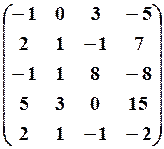
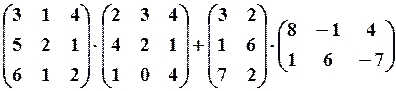
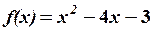 ,
,  9.6.
9.6. 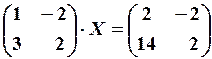
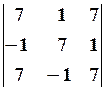 10.2.
10.2. 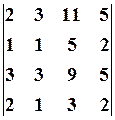 10.3.
10.3. 

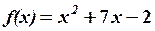 ,
,  10.6.
10.6. 
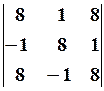 11.2.
11.2.  11.3.
11.3. 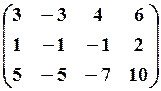
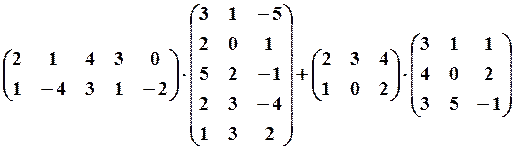
 ,
, 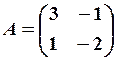 11. 6.
11. 6. 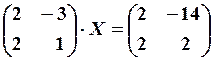
 12.2.
12.2.  12.3.
12.3. 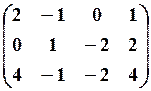
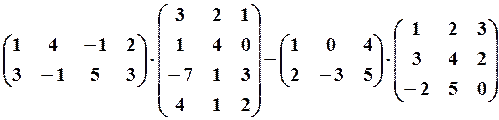
 ,
, 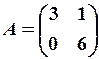 12.6.
12.6. 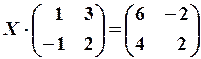
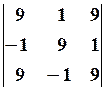 13.2.
13.2.  13.3.
13.3. 
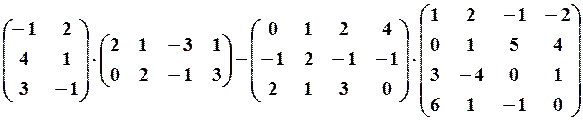
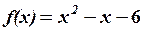 ,
, 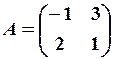 13.6.
13.6. 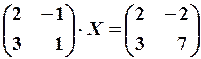
 14.2.
14.2.  14.3.
14.3. 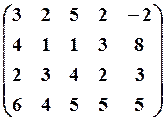
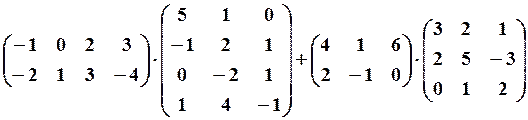
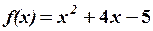 ,
, 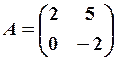 14.6.
14.6. 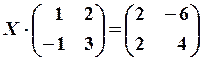
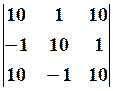 15.2.
15.2. 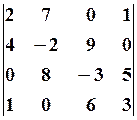 15.3.
15.3. 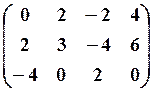

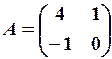 15.6.
15.6. 
 16.2.
16.2.  16.3.
16.3. 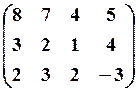

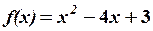 ,
, 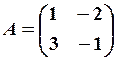 16.6.
16.6. 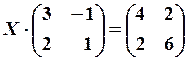
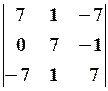 17.2.
17.2. 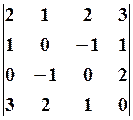 17.3.
17.3. 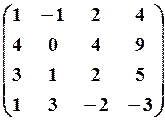

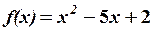 ,
, 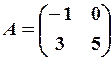 17.6.
17.6. 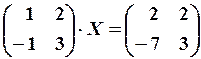
 18.2.
18.2. 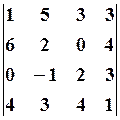 18.3.
18.3. 

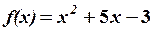 ,
, 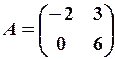 18.6.
18.6. 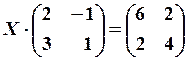
 19.2.
19.2.  19.3.
19.3. 

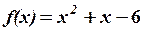 ,
, 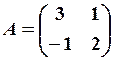 19.6.
19.6. 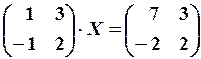
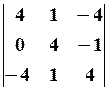 20.2.
20.2. 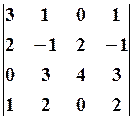 20.3.
20.3. 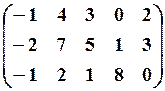

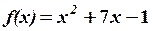 ,
, 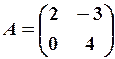 20.6.
20.6. 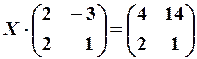
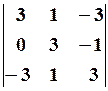 21.2.
21.2. 
 21.3.
21.3. 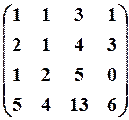

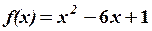 ,
, 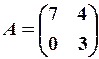 21.6.
21.6. 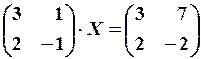
 22.2.
22.2. 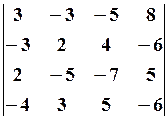 22.3.
22.3. 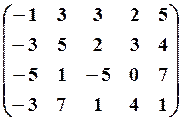

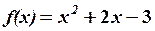 ,
, 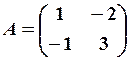 22.6.
22.6. 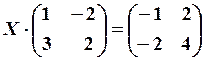
 23.2.
23.2.  23.3.
23.3. 

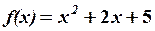 ,
, 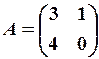 23.6.
23.6. 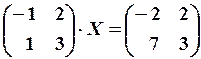
 24.2.
24.2.  24.3.
24.3. 
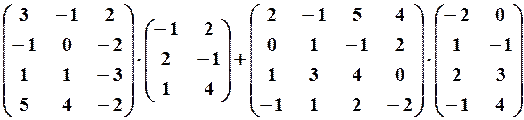
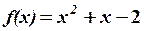 ,
, 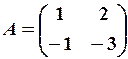 24.6.
24.6. 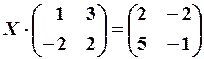
 25.2.
25.2.  25.3.
25.3. 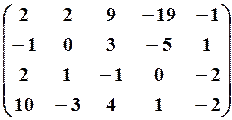
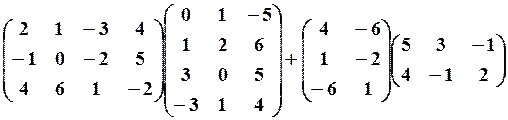
 25.6.
25.6. 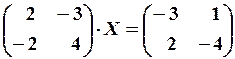
 26.3.
26.3. 

 ,
, 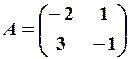 26.6.
26.6. 
 27.2.
27.2.  27.3.
27.3. 
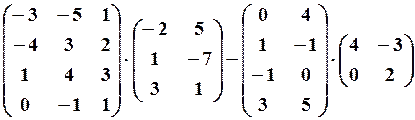
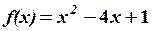 ,
, 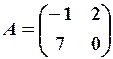 27.6.
27.6. 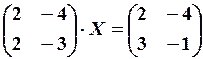
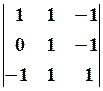 28.2.
28.2. 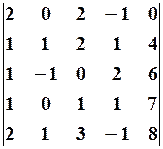 28.3.
28.3. 

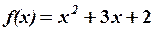 ,
,  28.6.
28.6. 
 29.2.
29.2. 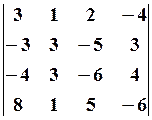 29.3.
29.3. 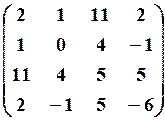

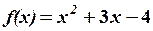 ,
, 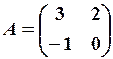 29.6.
29.6.  .
.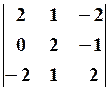 30.2.
30.2. 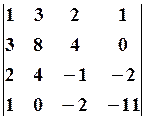 30.3.
30.3. 

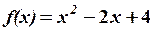 ,
,  30.6.
30.6.  .
. система рівнянь має нетривіальні (ненульові) розв’язки? Знайти ці розв’язки.
система рівнянь має нетривіальні (ненульові) розв’язки? Знайти ці розв’язки. .
. .
.
 .
. ;
; ;
; .
. .
. .
. ,
, , де
, де  ,
,  ,
,  .
. , то для матриці
, то для матриці  , звідки
, звідки  , або
, або  .
. ,
, ,
, ,
, .
. .
.
 .
. .
.


