
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунково-графічна робота №1Стр 1 из 3Следующая ⇒
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА №1
ЛІНІЙНА АЛГЕБРА
1.1 МАТРИЦІ І ВИЗНАЧНИКИ Завдання 1.1.
1. Обчислити визначник 3-го порядку, використовуючи метод Саррюса (або метод трикутників) і метод розкладання за мінорами для довільного ряду. 2. Обчислити визначник вищого порядку. 3. Привести матрицю до ступінчастого вигляду і обчислити ранг матриці. 4. Виконати дії з матрицями. 5. Обчислити значення многочлена від матриці 6. Знайти невідому матрицю Зразок розв’язання
1.Обчисліть визначник 3-го порядку: 1) за правилом Саррюса (або правило трикутників). Це правило полягає в наступній рівності:
Таким чином,
2) Друге правило обчислення називається розкладанням за елементами довільного рядка (або стовпця). Наприклад, розкладання за елементами першого рядка має вигляд:
Визначник
Розкладемо за елементами третього стовпця, тобто
Як видно з наведених прикладів, обчислення визначників значно спрощується, якщо ряд визначника має тільки один елемент, відмінний від нуля. Цього можна завжди досягти, використовуючи властивості визначників. У визначнику
помножимо перший рядок на 2 і додаємо до другого, додаємо перший рядок до третього, отримаємо
2. Обчислити визначник вищого порядку
Розв’язання:
Використовуючи властивості визначника, знизимо порядок визначника. З цією метою додаємо п'ятий стовпець до першого:
в отриманому визначнику 4-го порядку четвертий стовпець помножимо на 3 і додаєм до першого стовпця, потім помножимо його на 2 і додаєм до другого стовпця, помножимо його на 8 і додаємо до третього стовпця, отримуємо
З наведеного прикладу зрозуміло, що обчислення визначників вищих порядків значно спрощується, якщо визначник привести до трикутного вигляду.
3. Привести матрицю до ступінчастого вигляду і обчислити ранг матриці
Розв’язання.
Говорять, що квадратна матриця має східчастий вигляд, якщо нижче її головної діагоналі стоять нульові елементи. Матриця приводиться до східчастого виду і за допомогою елементарних перетворень: а) перестановка рядків, б) множення рядка на число, в) додавання до одного рядка іншого, помноженого на деяке число. Ранг матриці
У першому стовпці цієї матриці
Щоб отримати нулі в матриці до другої рядку додаємо третій рядок, помножений на (-1), результат напишемо на місці другого рядка. Далі, поділимо третій рядок на (-2), четвертий рядок на (-1), маємо
У другому стовпці отриманої матриці нижче другого елементу отримаємо нульові елементи. Послідовно помножимо другий рядок отриманої матриці на 2 і додаємо до третьому рядку, помножимо на 7 і додаємо до четвертого рядку, потім третій рядок поділимо на 9, четвертий рядок поділимо на 18. У новоствореній матриці в третьому стовпці нижче третього елемента отримаємо нульовий елемент: третій рядок помножимо на (-1) і додаємо до четвертого рядку, маємо
Звідки,
4. Виконати дії з матрицями
Розв’язання. Позначимо
Добуток
Добуток
Різниця
Відповідь: Результатом є матриця
5. Обчислити значення многочлена
Розв’язання. При обчисленні значення многочлена
1)
2)
3)
Маємо
Відповідь:
6. 1) Знайти невідому матрицю
Розв’язання. Індивідуальні завдання
Варіант № 1
1.1.
1.4.
1.5.
Варіант № 2
2.1.
2.4.
2.5.
Варіант № 3
3.1
3.4.
3.5.
Варіант № 4
4. 1.
4.4.
4.5.
Варіант № 5
5.1.
5.4.
5.5.
Варіант № 6
6.1.
6.4.
6.5.
Варіант № 7
7.1.
7.4.
7.5.
Варіант № 8
8.1.
8.4.
8.5.
Варіант № 9
9.1.
9.4.
9.5.
Варіант № 10
10.1.
10.4.
10.5.
Варіант № 11
11.1.
11.4.
11.5.
Варіант № 12
12.1.
12.4.
12.5.
Варіант № 13
13.1.
13.4.
13.5.
Варіант № 14
14.1.
14.4.
14.5.
Варіант № 15
15.1.
15.4.
15.5.
Варіант № 16
16.1.
16.4.
16.5.
Варіант № 17
17.1.
17.4.
17.5.
Варіант № 18
18.1.
18.4.
18.5.
Варіант № 19
19.1.
19.4.
19.5.
Варіант № 20
20.1.
20.4.
20.5.
Варіант № 21
21.1.
21.4.
21.5.
Варіант № 22
22.1.
22.4.
22.5.
Варіант № 23
23.1.
23.4.
23.5.
Варіант № 24
24.1.
24.4.
24.5.
Варіант № 25
25.1.
25.4.
25.5.
Варіант № 26
26.1.
26.4.
26.5.
Варіант № 27
27.1.
27.4.
27.5.
Варіант № 28
28.1.
28.4.
28.5.
Варіант № 29
29.1.
29.4.
29.5.
Варіант № 30
30.1.
30.4.
30.5.
1.2 СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ Завдання 1.2 Індивідуальні завдання
Варіант 1
1.1
1.3
Варіант 2
2.1
2.3
Варіант 3
3.1
3.3
Варіант 4
4.1
4.3
Варіант 5
5.1
5.3
Варіант 6
6.1
6.3
Варіант 7
7.1
7.3
Варіант 8
8.1
8.3
Варіант 9
9.1
9.3
Варіант 10
10.1
10.3
Варіант 11
11.1
11.3
Варіант 12
12.1
12.3
Варіант 13
13.1
13.3
Варіант 14
14.1
14.3
Варіант 15
15.1
15.3
Варіант 16
16.1
16.3
Варіант 17
17.1
17.3
Варіант 18
18.1
18.3
Варіант 19
19.1
19.3
Варіант 20
20.1
20.3
Варіант 21
21.1
21.3 Варіант 22
22.1
22.3
Варіант 23
23.1
23.3
Варіант 24
24.1
24.3
Варіант 25
25.1
25.3
Варіант 26
26.1
26.3
Варіант 27
27.1
27.3
Варіант 28
28.1
28.3
Варіант 29
29.1
29.3
Варіант 30
30.1
30.3
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА №1
ЛІНІЙНА АЛГЕБРА
1.1 МАТРИЦІ І ВИЗНАЧНИКИ Завдання 1.1.
1. Обчислити визначник 3-го порядку, використовуючи метод Саррюса (або метод трикутників) і метод розкладання за мінорами для довільного ряду. 2. Обчислити визначник вищого порядку. 3. Привести матрицю до ступінчастого вигляду і обчислити ранг матриці. 4. Виконати дії з матрицями. 5. Обчислити значення многочлена від матриці 6. Знайти невідому матрицю Зразок розв’язання
1.Обчисліть визначник 3-го порядку: 1) за правилом Саррюса (або правило трикутників). Це правило полягає в наступній рівності:
Таким чином,
2) Друге правило обчислення називається розкладанням за елементами довільного рядка (або стовпця). Наприклад, розкладання за елементами першого рядка має вигляд:
Визначник
Розкладемо за елементами третього стовпця, тобто
Як видно з наведених прикладів, обчислення визначників значно спрощується, якщо ряд визначника має тільки один елемент, відмінний від нуля. Цього можна завжди досягти, використовуючи властивості визначників. У визначнику
помножимо перший рядок на 2 і додаємо до другого, додаємо перший рядок до третього, отримаємо
2. Обчислити визначник вищого порядку
Розв’язання:
Використовуючи властивості визначника, знизимо порядок визначника. З цією метою додаємо п'ятий стовпець до першого:
в отриманому визначнику 4-го порядку четвертий стовпець помножимо на 3 і додаєм до першого стовпця, потім помножимо його на 2 і додаєм до другого стовпця, помножимо його на 8 і додаємо до третього стовпця, отримуємо
З наведеного прикладу зрозуміло, що обчислення визначників вищих порядків значно спрощується, якщо визначник привести до трикутного вигляду.
3. Привести матрицю до ступінчастого вигляду і обчислити ранг матриці
Розв’язання.
Говорять, що квадратна матриця має східчастий вигляд, якщо нижче її головної діагоналі стоять нульові елементи. Матриця приводиться до східчастого виду і за допомогою елементарних перетворень: а) перестановка рядків, б) множення рядка на число, в) додавання до одного рядка іншого, помноженого на деяке число. Ранг матриці
У першому стовпці цієї матриці
Щоб отримати нулі в матриці до другої рядку додаємо третій рядок, помножений на (-1), результат напишемо на місці другого рядка. Далі, поділимо третій рядок на (-2), четвертий рядок на (-1), маємо
У другому стовпці отриманої матриці нижче другого елементу отримаємо нульові елементи. Послідовно помножимо другий рядок отриманої матриці на 2 і додаємо до третьому рядку, помножимо на 7 і додаємо до четвертого рядку, потім третій рядок поділимо на 9, четвертий рядок поділимо на 18. У новоствореній матриці в третьому стовпці нижче третього елемента отримаємо нульовий елемент: третій рядок помножимо на (-1) і додаємо до четвертого рядку, маємо
Звідки,
4. Виконати дії з матрицями
Розв’язання. Позначимо
Добуток
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.183.137 (0.475 с.) |
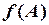 .
.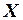 з рівняння
з рівняння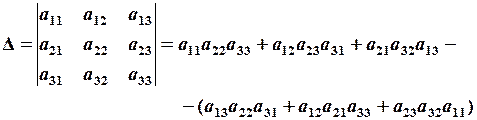 .
.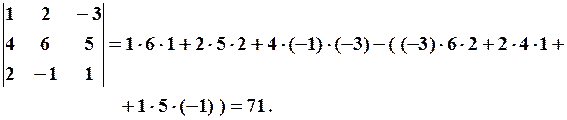
 .
.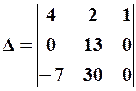
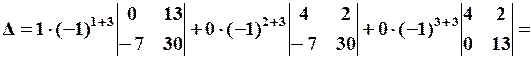
 .
.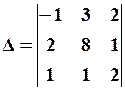
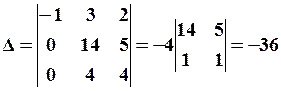 .
.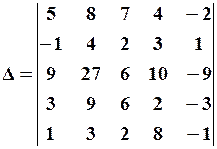 .
.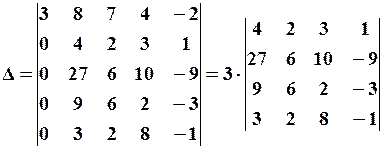 ;
;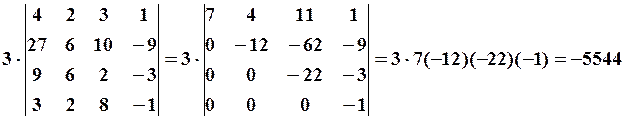 .
.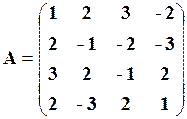 .
.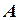 ,
, 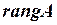 , дорівнює кількості ненульових рядків еквівалентної їй матриці східчастого виду.
, дорівнює кількості ненульових рядків еквівалентної їй матриці східчастого виду.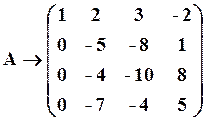 .
.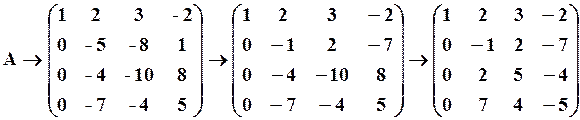 .
.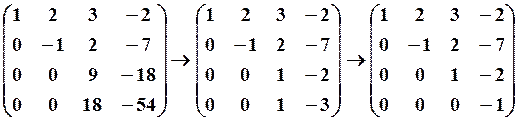 .
. .
.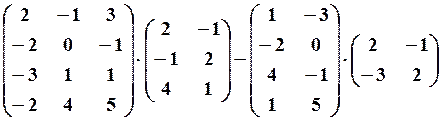 .
.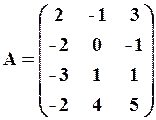 ,
, 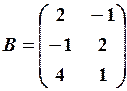 ,
,  ,
, 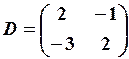 .
. має сенс, оскільки число стовпців матриці
має сенс, оскільки число стовпців матриці 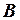 . Знаходимо матрицю
. Знаходимо матрицю 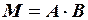 ,елементи якої
,елементи якої 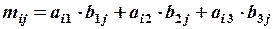 ,
, 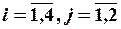 . Маємо
. Маємо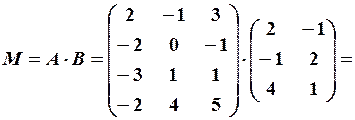
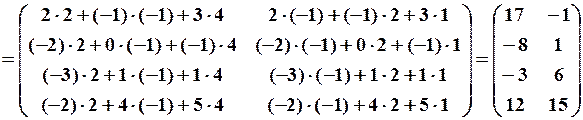 .
.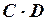 має сенс, оскільки таж кількість стовпчиків матриці
має сенс, оскільки таж кількість стовпчиків матриці 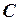 дорівнює числу рядків матриці
дорівнює числу рядків матриці  . Знаходимо матрицю
. Знаходимо матрицю  , елементи якої
, елементи якої 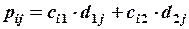 ,
, 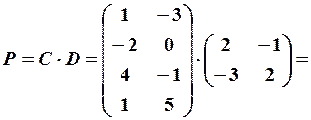
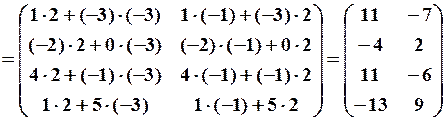 .
. має сенс, оскільки матриці
має сенс, оскільки матриці 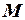 і
і  мають однакову розмірність
мають однакову розмірність 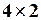 . Знаходимо шукану матрицю
. Знаходимо шукану матрицю 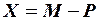 , елементи якої
, елементи якої 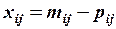 ,
, 
 .
. .
. від матриці
від матриці 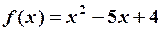 ,
, 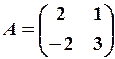 .
.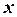 підставляємо дану матрицю
підставляємо дану матрицю  , де
, де 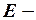 одинична матриця того ж порядку, що й дана матриця
одинична матриця того ж порядку, що й дана матриця 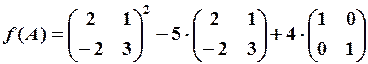 ,
,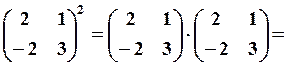
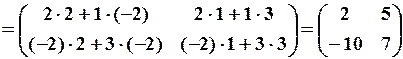 ,
,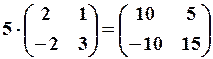 ,
, .
.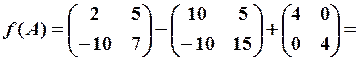
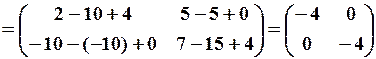 .
.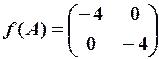 .
.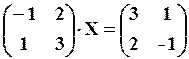 .
. 1.2.
1.2. 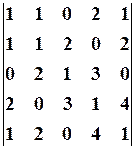 1.3.
1.3. 
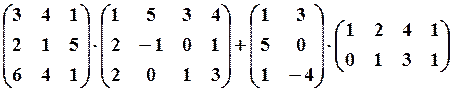
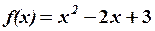 ,
,  1.6.
1.6. 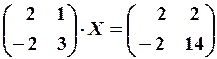
 2.2.
2.2. 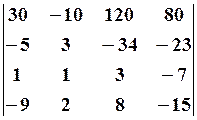 2.3.
2.3. 

 ,
, 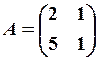 2.6.
2.6. 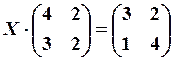
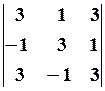 3.2.
3.2. 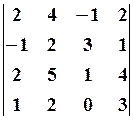 3.3.
3.3. 
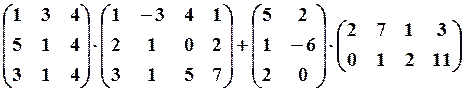
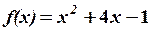 ,
, 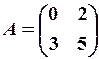 3.6.
3.6. 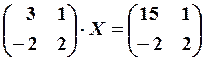
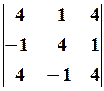 4.2.
4.2. 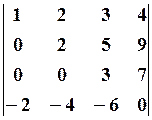 4.3.
4.3. 
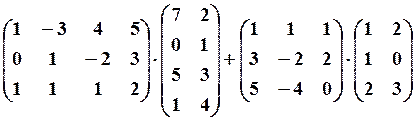
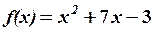 ,
,  4. 6.
4. 6. 
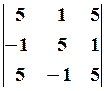 5.2.
5.2. 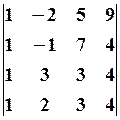 5.3.
5.3. 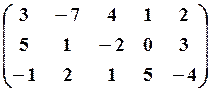
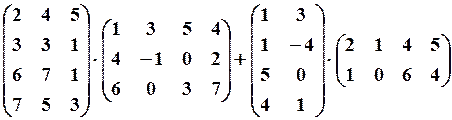
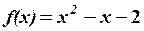 ,
, 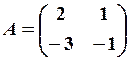 5.6.
5.6. 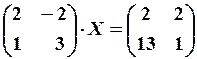
 6.2.
6.2. 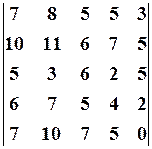 6.3.
6.3. 

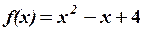 ,
, 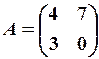 6.6.
6.6. 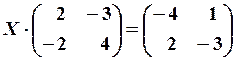
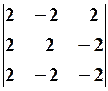 7.2.
7.2. 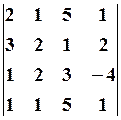 7.3.
7.3. 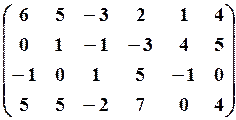
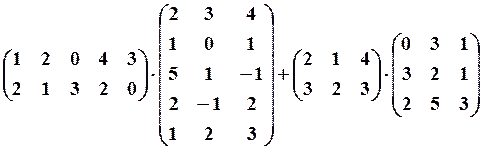
 ,
, 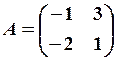 7. 6.
7. 6. 
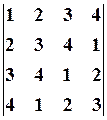 8.3.
8.3. 

 ,
, 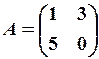 8.6.
8.6. 
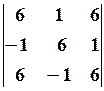 9.2.
9.2. 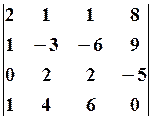 9.3.
9.3. 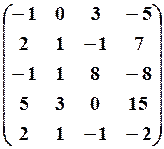
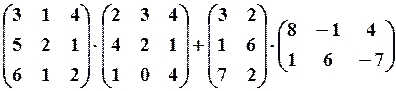
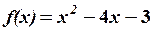 ,
,  9.6.
9.6. 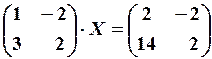
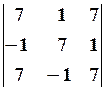 10.2.
10.2. 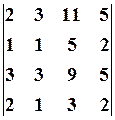 10.3.
10.3. 

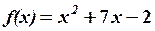 ,
,  10.6.
10.6. 
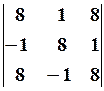 11.2.
11.2.  11.3.
11.3. 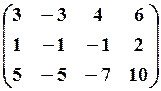
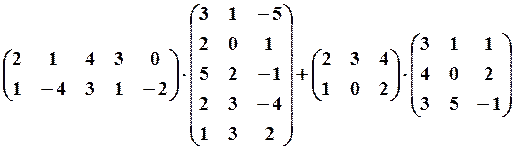
 ,
, 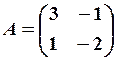 11. 6.
11. 6. 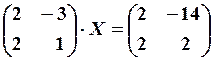
 12.2.
12.2.  12.3.
12.3. 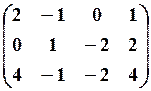
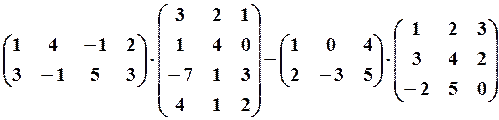
 ,
, 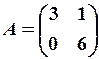 12.6.
12.6. 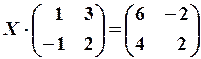
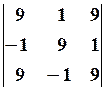 13.2.
13.2.  13.3.
13.3. 
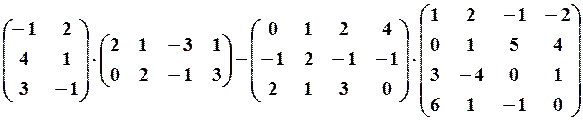
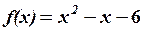 ,
, 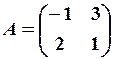 13.6.
13.6. 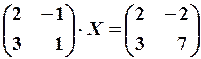
 14.2.
14.2.  14.3.
14.3. 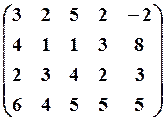
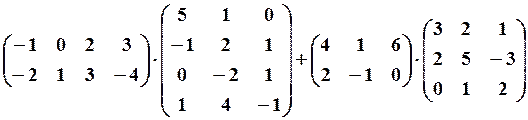
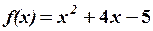 ,
, 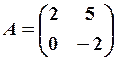 14.6.
14.6. 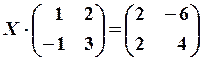
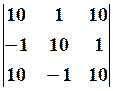 15.2.
15.2. 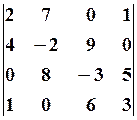 15.3.
15.3. 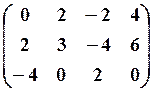

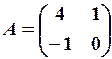 15.6.
15.6. 
 16.2.
16.2.  16.3.
16.3. 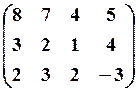

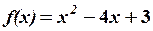 ,
, 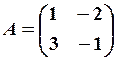 16.6.
16.6. 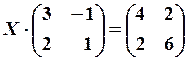
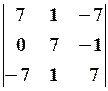 17.2.
17.2. 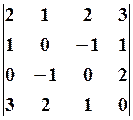 17.3.
17.3. 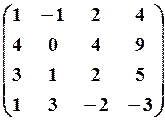

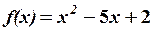 ,
, 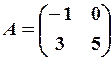 17.6.
17.6. 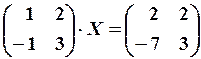
 18.2.
18.2. 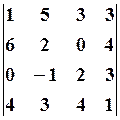 18.3.
18.3. 

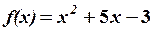 ,
, 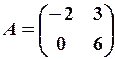 18.6.
18.6. 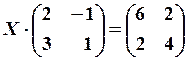
 19.2.
19.2.  19.3.
19.3. 

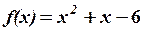 ,
, 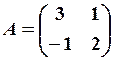 19.6.
19.6. 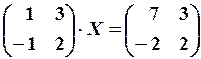
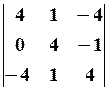 20.2.
20.2. 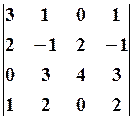 20.3.
20.3. 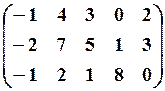

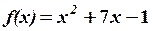 ,
, 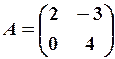 20.6.
20.6. 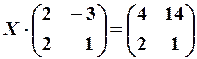
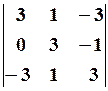 21.2.
21.2. 
 21.3.
21.3. 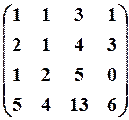

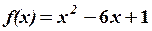 ,
, 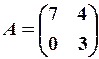 21.6.
21.6. 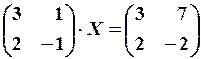
 22.2.
22.2. 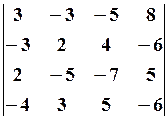 22.3.
22.3. 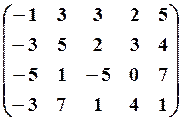

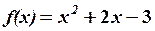 ,
, 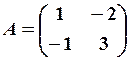 22.6.
22.6. 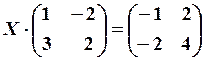
 23.2.
23.2.  23.3.
23.3. 

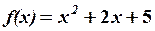 ,
, 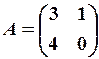 23.6.
23.6. 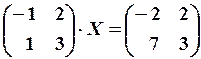
 24.2.
24.2.  24.3.
24.3. 
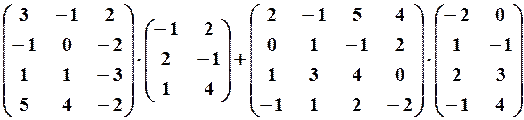
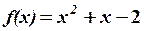 ,
, 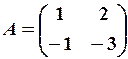 24.6.
24.6. 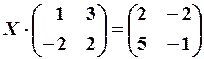
 25.2.
25.2.  25.3.
25.3. 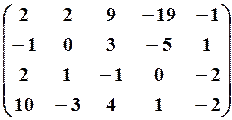
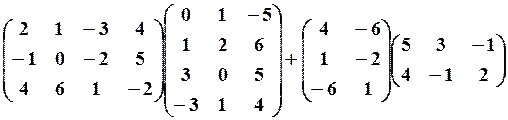
 25.6.
25.6. 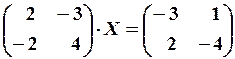
 26.3.
26.3. 

 ,
, 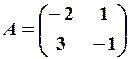 26.6.
26.6. 
 27.2.
27.2.  27.3.
27.3. 
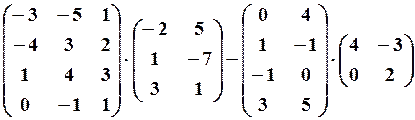
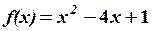 ,
, 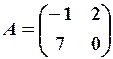 27.6.
27.6. 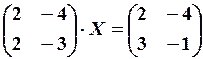
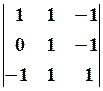 28.2.
28.2. 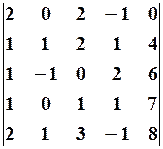 28.3.
28.3. 

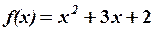 ,
,  28.6.
28.6. 
 29.2.
29.2. 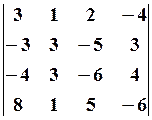 29.3.
29.3. 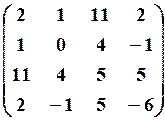

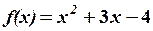 ,
, 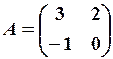 29.6.
29.6.  .
.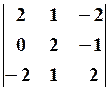 30.2.
30.2. 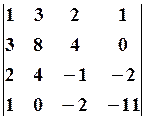 30.3.
30.3. 

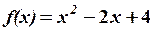 ,
,  30.6.
30.6.  .
.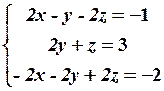 1.2
1.2 
 1.4
1.4 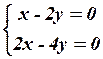 1.5
1.5 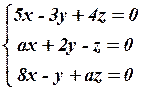
 2.2
2.2 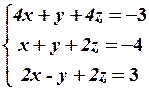
 2.4
2.4 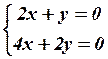 2.5
2.5 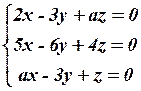
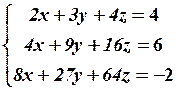 3.2
3.2 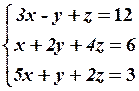
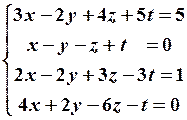 3.4
3.4  3.5
3.5 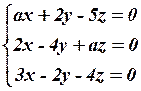
 4.2
4.2 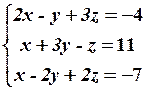
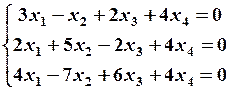 4.4
4.4 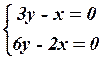 4.5
4.5 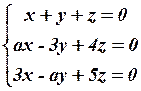
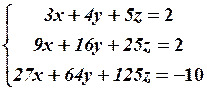 5.2
5.2 
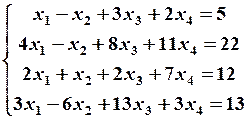 5.4
5.4  5. 5
5. 5 
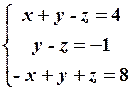 6.2
6.2 
 6.4
6.4 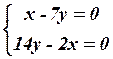 6.5
6.5 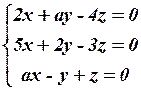
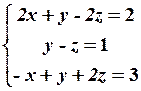 7.2
7.2 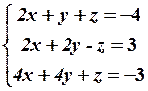
 7.4
7.4 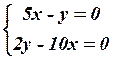 7.5
7.5 
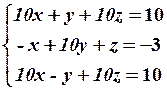 8.2
8.2 
 8.4
8.4 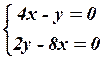 8.5
8.5 
 9.2
9.2 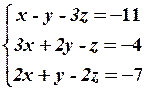
 9.4
9.4 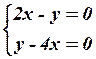 9.5
9.5 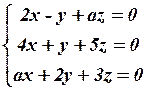
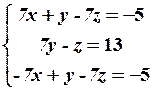 10.2
10.2 
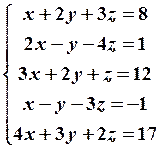 10.4
10.4  10.5
10.5 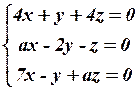
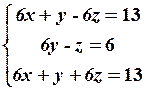 11.2
11.2 
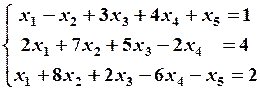 11.4
11.4 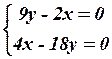 11.5
11.5 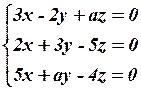
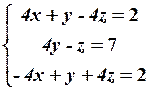 12.2
12.2 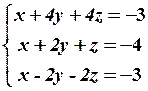
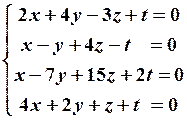 12.4
12.4 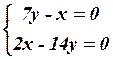 12.5
12.5 
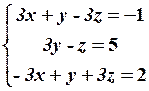 13.2
13.2 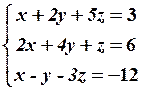
 13.4
13.4 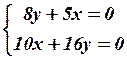 13.5
13.5 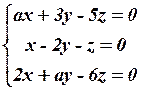
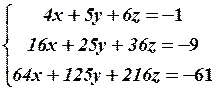 14.2
14.2 
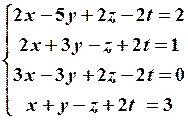 14.4
14.4 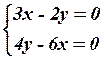 14.5
14.5 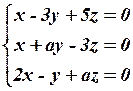
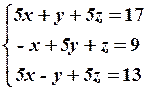 15.2
15.2 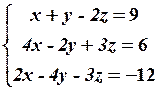
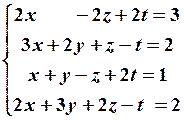 15.4
15.4 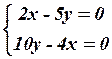 15.5
15.5 
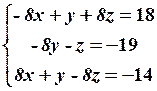 16.2
16.2 
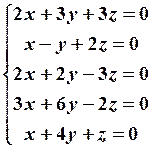 16.4
16.4 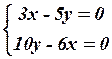 16.5
16.5 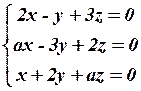
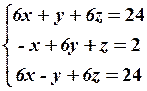 17.2
17.2 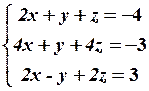
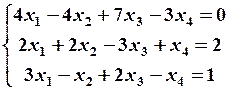 17.4
17.4 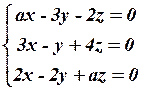
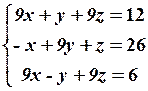 18.2
18.2 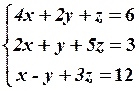
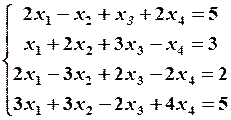 18.4
18.4  18.5
18.5 
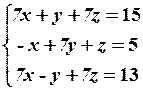 19.2
19.2 
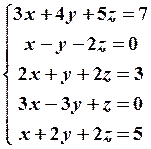 19.4
19.4  19.5
19.5 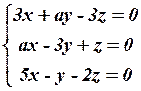
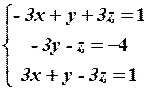 20.2
20.2 
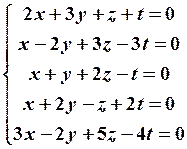 20.4
20.4 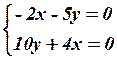 20.5
20.5 
 21.2
21.2 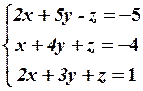
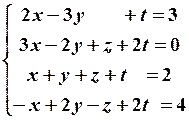 21.4
21.4 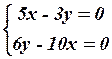 21.5
21.5 
 22.2
22.2 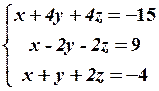
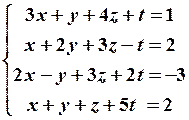 22.4
22.4 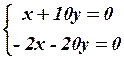 22.5
22.5 
 23.2
23.2 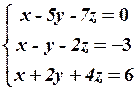
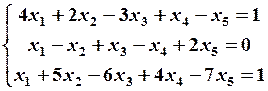 23.4
23.4  23.5
23.5 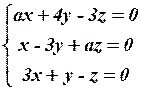
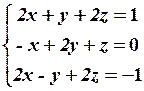 24.2
24.2 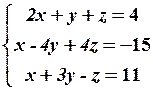
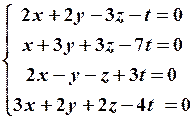 24.4
24.4 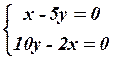 24.5
24.5 
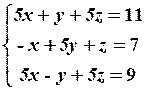 25.2
25.2 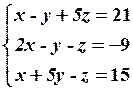
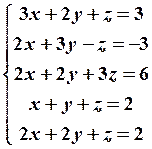 25.4
25.4  25.5
25.5 
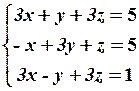 26.2
26.2 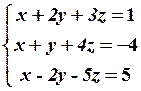
 26.4
26.4 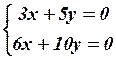 26.5
26.5 
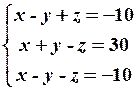 27.2
27.2 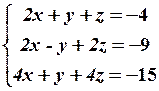
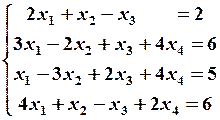 27.4
27.4 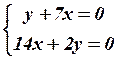 27.5
27.5 
 28.2
28.2 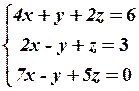
 28.4
28.4  28.5
28.5 
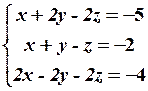 29. 2
29. 2 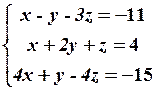
 29.4
29.4 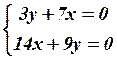 29.5
29.5 
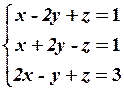 30.2
30.2 
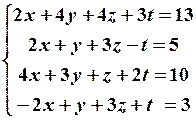 30.4
30.4 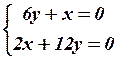 30.5
30.5  .
.


