
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение и устройство аэродинамической трубы
Большинство задач экспериментальной механики жидкости и газа связано с изучением движения тел с некоторой скоростью Обращенное движение изучается в специальных устройствах – аэродинамических или гидродинамических трубах. Исследуемое тело располагают в рабочем участке трубы и затем перед ним создают равномерный, прямолинейный, установившийся поток жидкости или газа с постоянной скоростью. Схема простейшей аэродинамической трубы малых скоростей, используемой для проведения лабораторных работ, представлена на рис. 1.1. Неподвижный воздух засасывается из помещения лаборатории вентилятором 12, установленным на выходе из трубы, и поступает в сопло 2. Сопло ускоряет поток и создает на входе в рабочий участок однородное поле скоростей (V 0»20 м/с). В закрытом рабочем участке 4 прямоугольного поперечного сечения для испытаний устанавливаются обтекаемые тела: крыловые профили, пластины и т.д. Диффузор 9 преобразует кинетическую энергию выходящего из рабочего участка потока в энергию давления, уменьшая потери энергии в трубе. Для предотвращения отрыва потока в диффузоре по его длине установлены три сетки 7. К рабочему участку и потоку в нём предъявляются следующие требования: 1. Однородность. 2. Малое изменение распределений скоростей и давлений по длине рабочего участка. 3. Низкая турбулентность набегающего потока. 4. Стационарность. 5. Границы рабочего участка не должны существенно влиять на обтекание тел, что требует применения рабочих участков, размеры которых велики по сравнению с размерами обтекаемых тел.
2. Измерение параметров потока и контрольно‑измерительные приборы
При вычислении давлений в потоке сжимаемого воздуха с некоторой погрешностью можно пренебрегать изменением плотности и пользоваться уравнением Бернулли для несжимаемой жидкости. Погрешность уменьшается с уменьшением числа Маха М= V 0/ a, представляющего собой отношение скорости жидкости V 0 к скорости звука a. При скорости V 0=68 м/с и a =340 м/с число М=0,2 и, как показывают расчеты, погрешности вычисления давлений и плотностей не превышают 1 и 2% соответственно. В данной аэродинамической трубе, где V 0<40 м/с, указанные погрешности будут еще меньшими. Температура воздуха t в градусах Цельсия измеряется термометром 14. Абсолютная температура в градусах Кельвина: T =(273+ t) K (1.1) Атмосферное давление p ат в Па определяется по барометру. Плотность r в кг/м3 вычисляется по уравнению состояния идеальных газов r= p / RT, (1.2) где p = p ат – абсолютное давление воздуха, Па; R =287,14 Дж/кг×К– газовая постоянная воздуха.
Динамическая вязкость воздуха m при умеренных давлениях не зависит от давления и увеличивается с ростом температуры t. Эта зависимость показана на рис. 1.2. (Единицей динамической вязкости в системе СИ является 1 паскаль–секунда=1 кг/м×с=1 Па×с).
Избыточные давления или вакуумы измеряются чашечными микроманометрами с наклонной трубкой (рис.1.3). Избыточное давление или вакуум в Па равны: p и= - p в=rр glK, (1.3) где K =sin a – постоянная микроманометра; a– угол наклона трубки микроманометра к горизонту; rр= 790 кг/м3 – плотность рабочей жидкости микроманометра; g =9.81 м/с2 – ускорение свободного падения; l – отсчет по шкале микроманометра, м. С уменьшением угла a точность измерения заданного давления возрастает, так как при этом увеличивается l. Скорость набегающего потока V 0 в м/с в рабочем участке находим по падению давления на сопле. Составим уравнение Бернулли для двух точек линии тока, показанной на рис. 1.1. Одну точку выберем на удалении от сопла в помещении лаборатории, где давление равно атмосферному p ат, а скорость равна нулю. Другую точку – на входе в рабочий участок, где давление p 0, а скорость V 0. Уравнение Бернулли примет вид:
p ат= p 0+ r V 02/2+ z r V 02/2, где r– плотность воздуха; z– коэффициент потерь энергии. Из этого уравнения получаем
где D p 0= p ат- p 0 – падение давления на сопле. Измерения показали, что с погрешностью не более 0.5% можно принять z=0. Так как в соответствии с (1.3) D p 0=rр gl 0 K 0, то
и r V 02/2=rр gl 0 K 0 (1.5)
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.203.143 (0.006 с.) |
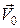 в неподвижной на бесконечно большом удалении от тел среде (движение судна, движение крыла самолета и т.п.). Если ко всем частицам жидкости и точкам тела добавить такую же по величине, но противоположную по направлению скорость –
в неподвижной на бесконечно большом удалении от тел среде (движение судна, движение крыла самолета и т.п.). Если ко всем частицам жидкости и точкам тела добавить такую же по величине, но противоположную по направлению скорость – 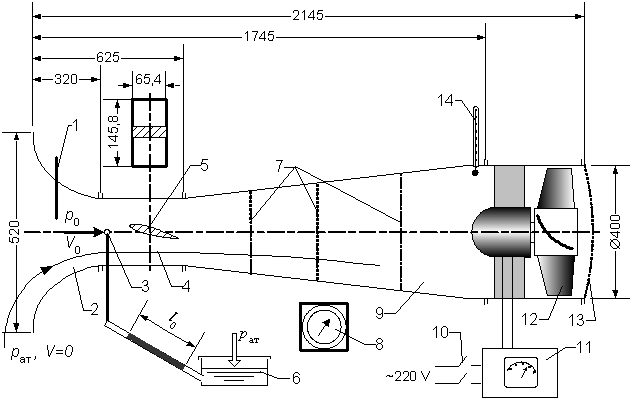


 ,
,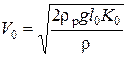 (1.4)
(1.4)


