
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр класса, дисперсия и среднеквадратичное отклонение
Пусть имеется некоторый класс
Центром класса
Таким образом, центр класса
Дисперсия – это мера «размытости» класса, или мера отклонения значений существенных признаков объектов от центра данного класса. В
Здесь, как и раньше, Стандартным или среднеквадратичным отклонением называется корень квадратный из дисперсии
Эта величина измеряется в тех же единицах, что и среднее значение существенных признаков данного класса. 2.3.1.2. Скейлинг (масштабное преобразование) и стандартизованное расстояние В общем случае значения существенных признаков, подаваемые на вход системы классификации, являются размерными величинами. Например, это может быть сила тока, измеряемая датчиком в некоторых единицах, предположим в амперах. Следовательно, в этом случае и расстояния между объектами и центрами классов будут измеряться в амперах. Дисперсия тогда будет измеряться в Чтобы сделать расстояние безразмерной величиной, т.е. не зависящей от единицы измерения существенных признаков, произведем масштабное преобразование расстояния. Для этого разделим обычное расстояние
Безразмерная величина
Приведем в развернутом виде формулу для вычисления стандартизованного расстояния между объектом
Здесь компоненты
где Для иллюстрации понятия скейлинга рассмотрим следующий пример. Более характерной для скейлинга является следующая ситуация. Предположим, что системе для распознавания предъявлены три треугольника - Ковариационная матрица Ковариация – это численное выражение свойства ковариантности двух существенных признаков объектов. Свойство ковариантности означает, что признаки имеют тенденцию изменяться совместно (ковариантно). В этом случае, говорят еще, что признаки коррелируют. Пусть, например, к некоторому классу принадлежат три объекта:
Ковариационная матрица состоит из ковариаций между всеми парами существенных признаков объектов, относящихся к одному классу. Пусть количество существенных признаков равно
Элементы ковариационной матрицы – ковариации – для объектов
где Ковариации обладают следующими важными свойствами: – если при переходе от одного объекта класса к другому – если при переходе от одного объекта класса к другому – если при переходе от одного объекта класса к другому – –
Таким образом, ковариация 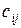 представляет собой число в интервале представляет собой число в интервале  , которое является мерой корреляции между , которое является мерой корреляции между  -ым и -ым и  -ым существенными признаками, причем, -ым существенными признаками, причем,  , если , если  -ый и -ый и  -ый существенные признаки независимы. Соответствие между ковариацией и формой класса объектов показано на рис. 2.11. -ый существенные признаки независимы. Соответствие между ковариацией и формой класса объектов показано на рис. 2.11.
Отметим, что ковариационная матрица 1. Если количество объектов 2. Если степень корреляции существенных признаков максимальна, т.е. В этих двух случаях нельзя обратить матрицу
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.60 (0.048 с.) |
 , который содержит
, который содержит  объектов, у каждого из которых
объектов, у каждого из которых  существенных признаков, то есть
существенных признаков, то есть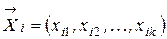 ,
,  ,
,  .
. является вектор
является вектор  , компоненты которого – средние значения одноименных, существенных признаков всех объектов данного класса. Другими словами, с редним значением
, компоненты которого – средние значения одноименных, существенных признаков всех объектов данного класса. Другими словами, с редним значением  того класса является арифметическое среднее:
того класса является арифметическое среднее: . (2.8)
. (2.8) .
.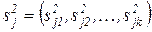 , причем элементы этой матрицы - дисперсии
, причем элементы этой матрицы - дисперсии  того признака - определяются из соотношения:
того признака - определяются из соотношения: . (2.9.)
. (2.9.) , причем среднеквадратическое отклонение
, причем среднеквадратическое отклонение  . (2.10.)
. (2.10.) , а среднеквадратичное отклонение в амперах. Если же значения существенных признаков измеряются в вольтах, то в тех же единицах будут измеряться и расстояние, среднее значение и среднеквадратичное отклонение.
, а среднеквадратичное отклонение в амперах. Если же значения существенных признаков измеряются в вольтах, то в тех же единицах будут измеряться и расстояние, среднее значение и среднеквадратичное отклонение.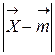 на среднеквадратичное отклонение
на среднеквадратичное отклонение  :
: . (2.11)
. (2.11) называется стандартизованным расстоянием.
называется стандартизованным расстоянием. и некоторым классом
и некоторым классом  .(2.11а)
.(2.11а) среднеквадратического отклонения
среднеквадратического отклонения  для класса
для класса 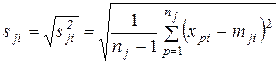 ,
, - дисперсия
- дисперсия  - количество объектов в данном классе.
- количество объектов в данном классе. ,
,  и
и  . Причем вследствие, например, ошибок измерения длины сторон этих треугольников принимают следующие значения:
. Причем вследствие, например, ошибок измерения длины сторон этих треугольников принимают следующие значения: 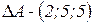 ,
,  и
и  . Очевидно, что эти треугольники подобны и могут быть отнесены к одному и тому же классу. Но, поскольку, они имеют разные длины сторон, эти треугольники могут, при определенных условиях, восприниматься системой классификации как объекты, принадлежащие разным классам. С другой стороны, необходимо использовать, в определенной степени, сложные решающие правила, учитывающие подобие треугольников. Чтобы в данной ситуации упростить процедуру классификации и сделать ее более надежной, поступим следующим образом: выберем в каждом треугольнике наибольшую сторону, а затем разделим все его стороны на наибольшую. В результате получим треугольники со сторонами:
. Очевидно, что эти треугольники подобны и могут быть отнесены к одному и тому же классу. Но, поскольку, они имеют разные длины сторон, эти треугольники могут, при определенных условиях, восприниматься системой классификации как объекты, принадлежащие разным классам. С другой стороны, необходимо использовать, в определенной степени, сложные решающие правила, учитывающие подобие треугольников. Чтобы в данной ситуации упростить процедуру классификации и сделать ее более надежной, поступим следующим образом: выберем в каждом треугольнике наибольшую сторону, а затем разделим все его стороны на наибольшую. В результате получим треугольники со сторонами:  ,
,  и
и  . Таким образом, после выполненного масштабного преобразования имеем три равных треугольника.
. Таким образом, после выполненного масштабного преобразования имеем три равных треугольника. ,
,  ,
,  . Как видно, при переходе от первого объекта к третьему значения первого и второго существенных признаков возрастают, то есть признаки изменяются совместно или ковариантно. Аналогичная ковариантность признаков будет наблюдаться и в таком случае
. Как видно, при переходе от первого объекта к третьему значения первого и второго существенных признаков возрастают, то есть признаки изменяются совместно или ковариантно. Аналогичная ковариантность признаков будет наблюдаться и в таком случае  ,
,  . Здесь первый признак возрастает, а второй убывает, однако между ними также существует сильная корреляция. Если же существенные признаки объектов имеют, например, такие значения
. Здесь первый признак возрастает, а второй убывает, однако между ними также существует сильная корреляция. Если же существенные признаки объектов имеют, например, такие значения  ,
,  ,
,  , то они не коррелируют между собой и, следовательно, изменяются не ковариантно.
, то они не коррелируют между собой и, следовательно, изменяются не ковариантно.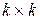 , имеющая вид:
, имеющая вид: .
. -того класса вычисляются по формуле:
-того класса вычисляются по формуле: , (2.12)
, (2.12) - номер объекта данного класса,
- номер объекта данного класса, 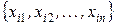 и
и  - множества, состоящее из
- множества, состоящее из  значений соответственно
значений соответственно  и
и  - средние значения соответственно
- средние значения соответственно  ;
; ;
; ;
; , где
, где  и
и  – стандартные отклонения
– стандартные отклонения  , где
, где  – дисперсия
– дисперсия 
 будет вырожденной в следующих двух случаях:
будет вырожденной в следующих двух случаях: .
. .
. .
.


