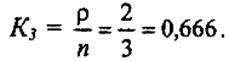Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многоканальная СМО с неограниченной очередью
На многоканальную СМО с ожиданием и неограниченной длиной очереди поступает поток заявок с интенсивностью λ, интенсивность обслуживания каждого канала μ. Размеченный граф состояний представлен на рисунке.
Граф СМО имеет бесконечное число состояний: S0 - все каналы свободны, k= 0; S1 - занят один канал, остальные свободны, k = 1; S2 - заняты два канала, остальные свободны, k = 2; ………………… Sn - заняты все n каналов, k = n, очереди нет; ………………. Sn+1 - заняты все n каналов, одна заявка в очереди, Sn+r - заняты все n каналов, r заявок в очереди, k = n + r;
Вероятности состояний получим из формул для многоканальной СМО с ограниченной очередью при переходе к пределу при m → ∞. Сумма геометрической прогрессии в выражении для р0 расходится при уровне загрузки р/n ≥1, очередь будет бесконечно возрастать, а при p/n < 1 ряд сходится, что определяет установившийся стационарный режим работы СМО, для которого и определим выражения для предельных вероятностей состояний:
Поскольку отказа в обслуживании в таких системах не может быть, то характеристики пропускной способности равны: ротк = 0; Q =1; A = λ·Q =λ; среднее число заявок в очереди – среднее время ожидания в очереди – среднее число заявок в СМО – Lсмо = Lоч + ρ. Вероятность того, что СМО находится в состоянии So, когда нет заявок и не занято ни одного канала, определяется выражением
Эта вероятность определяет среднюю долю времени простоя канала обслуживания. Вероятность занятости обслуживанием к заявок – На этом основании можно определить вероятность, или долю времени занятости всех каналов обслуживанием. Если же все каналы уже заняты обслуживанием, то вероятность состояния определяется выражением Вероятность оказаться в очереди равна вероятности застать все каналы уже занятыми обслуживанием. Среднее число заявок, находящихся в очереди и ожидающих обслуживания, равно: среднее время ожидания заявки в очереди начала обслуживания: среднее время пребывания заявки в СМО – среднее число занятых каналов обслуживанием равно - среднее число свободных каналов - коэффициент занятости каналов обслуживанием - среднее число заявок в СМО - Важно заметить, что параметр р характеризует степень согласования входного потока, например, покупателей в магазине с интенсивностью потока обслуживания. Процесс обслуживания будет стабилен при р < n. Если же р ≥ n, в системе будут возрастать средняя длина очереди и среднее время ожидания покупателями начала обслуживания, и, следовательно, СМО будет работать неустойчиво.
Пример 1. В столовой к узлу расчета поступает пуассоновский поток посетителей с интенсивностью λ = 120 человек в час. Средняя продолжительность обслуживания контролером-кассиром одного посетителя составляет Тобс = 1,0 мин. Определим оптимальное число контролеров-кассиров n0, при котором общие издержки С, определяемые затратами, с одной стороны, на содержание контролеров-кассиров Сио, а с другой - пребыванием посетителей в очереди Сип, были бы минимальны. На этом основании целевую функцию можно записать так: С=(Сио + Сип) → min Издержки Сио определяются числом каналов обслуживания n, величиной затрат, связанных с содержанием в системе одной обслуживающей единицы в течение одной единицы времени Ск (руб./ч) и интенсивностью входного потока λ. Сип определяются величиной удельных потерь Cоч связанных с пребыванием в очереди одного покупателя в течение единицы времени и средним временем ожидания в очереди Точ. Тогда целевую функцию затрат, связанную с пребыванием покупателей в системе в течение единицы времени, можно записать так: C = (Cк·n·1/λ + Соч tоч) → min, Для удобства проведения вычислений предположим, что Соч/Ск = 3/1, что позволит определить соотношение стоимостей обслуживания для разных вариантов организации системы. Для наглядности решения задачи построим график целевой функции С = f(n), по которому найдем минимум затрат, величина которого укажет на оптимальную численность контролеров-кассиров. Следует заметить, что длина очереди - один из основных показателей эффективности СМО. Причем если длина очереди в системе может бесконечно возрастать, то рациональной организации системы нельзя получить. Только при условии р < n очередь может быть конечна, т. е. число заявок, поступающих в СМО за промежуток времени, равный средней длительности обслуживания То6с, меньше числа обслуживающих каналов. Это обусловлено вероятностным характером как потока заявок, так и временем их обслуживания. Поэтому о рациональности варианта организации СМО можно рассуждать лишь в том случае, если n > р. Поскольку из условия задачи следует, что интенсивность нагрузки р = λ/μ = 2, то вычисления показателей системы следует начать с n = 3.
Сначала определяем долю времени простоя контролеров-кассиров в течение рабочего дня, т.е. при условии отсутствия покупателей.
Следовательно, 3 контролера-кассира будут простаивать 11 % времени от всей продолжительности рабочего дня. Результаты вычислений
Вероятность застать всех контролеров-кассиров занятыми определяется по формуле Эрланга.
Вероятность оказаться в очереди -
среднее число покупателей, находящихся в очереди, -
среднее время ожидания покупателями в очереди начала обслуживания -
относительная величина затрат для n = 3 и Соч = 3Ск составляет:
среднее время пребывания посетителя в узле расчета –
среднее число занятых обслуживанием контролеров-кассиров-
среднее число свободных контролеров-кассиров –
Коэффициент занятости контролеров-кассиров обслуживанием, т. е. нагрузка на одного контролера-кассира, или доля занятых обслуживанием каналов, составляет
Среднее число покупателей в узле расчета -
абсолютная пропускная способность узла расчета в столовой -
Затем проводим аналогичные вычисления по определению перечисленных показателей для других значений n = 4, 5, 6, 7 Оптимальное число контролеров-кассиров в узле расчета n° = 4 для соотношения Соч: Сk = 3: 1, при этом общие затраты будут минимальными.
Графическая модель связи относительно затрат СМО и числа кассиров Для целей расширения анализа проведены вычисления для разных вариантов соотношения Соч: Ck = 4,5, которое, влияет на оптимальную численность контролеров-кассиров.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.0.61 (0.009 с.) |

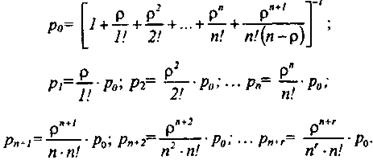
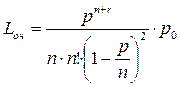 ;
;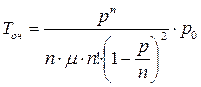
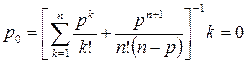
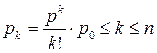 .
. .
.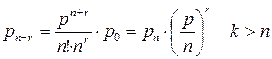
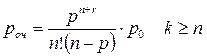
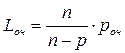
 ;
;