
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория массового обслуживания в исследовании процессов управления
Теория массового обслуживания в исследованиях процессов управления(ТМО) – это область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно. Основная задача ТМО сводится к определению оптимального соотношения между входным потоком требований и числом обслуживающих каналов, при котором общие суммарные затраты минимальны.
Общие суммарные затраты складываются из затрат обслуживания и затрат ожидания, причём по мере улучшения сервиса затраты обслуживания увеличиваются, а затраты ожидания уменьшаются. СМО (система массового обслуживания) можно описать с помощью следующих элементов: ü Входной поток требований характеризуется вероятностным законом распределения моментов поступления требований системы и количеством требований в каждом поступлении. В настоящее время теоретически наиболее разработанной и удобной в практическом применении методы решения таких задач, в которых поток требований является простейшим (пуассоновским). Пуассоновский поток обладает 3 свойствами: 1. Стационарностью – постоянным количеством событий в единицу времени 2. Отсутствие последействия – независимость количества событий после любого момента времени от количества событий до него 3. Ординарность – практическая невозможность одновременного поступления нескольких требований. Для простейшего случая частота наступления событий подчиняется закону Пуассона Рк(t)= Вероятность того, что произойдёт к-событий, где лямбда – количество событий в единицу времени (интенсивность потока). Пуассоновский поток заявок удобен при решении задач ТМО. Простейшие потоки редки на практике, однако многие моделируют потоки допустимо рассматривать как простейшие ü Дисциплина очереди описывает порядок обслуживания требований системы, длина очереди может быть ограниченной или неограниченной. Правила постановки в очередь, а также по другим приоритетам ü Механизм обслуживания характеризуется продолжительностью процедур обслуживания и количеством одновременно обслуживаемых требований. Время обслуживания требований к системе является случайной величиной и обычно описывается экспоненциальным законом распределения. Вероятность того, что время обслуживания не превосходит некоторые величины t проверяется выражением:
F(t)=1- µ – величина обратная времени обслуживания. Введём параметр a – коэффициент загрузки системы или среднее число каналов, которое необходимо иметь, чтобы обслужить в единицу времени все поступающие требования: а=λ**tобслуживания λ – среднее число требований, поступающих в единицу времени, µ – среднее число требований, удовлетворяемых в единицу времени, t обслуживания – среднее время обслуживания 1 каналом 1 требования. Если а меньше количества каналов обслуживания, то очередь не может расти безгранично, т.о. число обслуживающих каналов должно быть больше среднее числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступающие требования. 36.ТМО. Основные понятия (входной поток, дисциплина очереди, механизм обслуживания). ТМО- область прикладной математики, занимабщаяся анализом процессов в системах производства, обсуживния м управления, в к-х однородные события повторяются многократно. основная задача теории масс обсл сводится к определению оптимального соотношения между входным потоком требований и числом обслуживащих каналов, при которых общие суммарные затраты миню. Общая сумма затрат складывается из затрат обслуживания и затрат ожидания. Этапы сист масс обсл: входной поток требований, дисциплина очереди, механизм обслуживания. Входной поток –характся вероят-ным законом распределения в моменты поступления требований в систему и ком-ом требований. Простейщий поток облад 3-мя свойствами: 1) стационарность-пост. Кач-во событий в единицу времени отсутствие последствия-независимость количества событий после любого момента времени от количества событий до него. 2) Однородность-практическая невозможность одновременного поступления нескольких требований.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.112.111 (0.007 с.) |

 Входной поток требований Канал
Входной поток требований Канал









 Выходной поток
Выходной поток

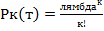 *
* 



