
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о методе наименьших квадратов ⇐ ПредыдущаяСтр 7 из 7
Пусть проводится серия из
где коэффициенты В общем случае в силу ошибок в измерениях при проведении опытов или «несовершенства» выбранной системы функций
Сформируем разности между левыми и правыми частями приближенных равенств (6.14)
Очевидно, если бы удалось подобрать систему функций
называемый вектором невязки, состоял бы из нулевых элементов и его длина была бы минимально возможной (равной нулю). Теперь мы можем уточнить, что следует понимать под приближением «наилучшим образом» зависимости
была минимально возможной для данной системы функций
Ясно, что если
Дифференцируя правую часть формулы (6.17) по переменным
¼ ¼ ¼ ¼ ¼ ¼
Сокращая на 2 обе части полученных равенств и записывая их в компактной форме, получаем систему
Раскрывая скобки и перенося известные величины в правые части, в итоге получаем систему, которая называется системой нормальных уравнений:
Заметим, что система (6.19) получена из необходимых условий экстремума функции Рассмотренный метод нахождения наилучшего в указанном смысле приближения к неизвестной функциональной зависимости
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.161.222 (0.004 с.) |
 опытов. Результатами наблюдений являются численные значения
опытов. Результатами наблюдений являются численные значения  некоторой величины. Поставим задачу: представить приближенным способом измеряемую величину
некоторой величины. Поставим задачу: представить приближенным способом измеряемую величину 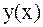 в виде линейной комбинации известных (базисных) функций –
в виде линейной комбинации известных (базисных) функций – 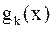 ,
,  ,
,  , так, чтобы полученная зависимость согласовывалась с результатами наблюдений «наилучшим образом». Словосочетание «наилучшим образом» будет далее пояснено. Итак, будем искать зависимость
, так, чтобы полученная зависимость согласовывалась с результатами наблюдений «наилучшим образом». Словосочетание «наилучшим образом» будет далее пояснено. Итак, будем искать зависимость 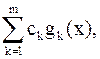
 подлежат определению.
подлежат определению.

 ,
, . Будем требовать, чтобы длина вектора
. Будем требовать, чтобы длина вектора 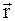 , которая вычисляется по формуле
, которая вычисляется по формуле ,
,
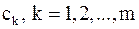 . Далее вместо длины вектора
. Далее вместо длины вектора 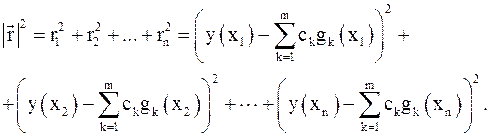
 минимален, то и выбор коэффициентов
минимален, то и выбор коэффициентов  переменных, в роли которых выступают коэффициенты
переменных, в роли которых выступают коэффициенты 

 ,
,
 ,
,



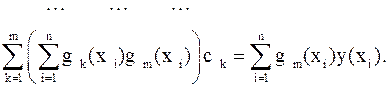
 , однако, ввиду громоздкости выкладок, мы этот вопрос здесь не рассматриваем.
, однако, ввиду громоздкости выкладок, мы этот вопрос здесь не рассматриваем. , если задана система базисных функций
, если задана система базисных функций  , основанный на нахождении решения системы уравнений (6.19), называется методом наименьших квадратов.
, основанный на нахождении решения системы уравнений (6.19), называется методом наименьших квадратов.


