
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вариационно-итерационные методы решения СЛАУ
Преимущество данных методов – они не используют никакой дополнительной информации об операторе 1. Метод минимальных невязок.
Для
Меняя знаки и группируя слагаемые соответствующим образом, получаем:
Параметр
Продифференцируем
2. Метод скорейшего спуска. Получается из условия минимума энергетической нормы погрешности
Дифференцируя
Пример выполнения лабораторной работы №4
Решите систему уравнений методом Якоби, Зейделя, наименьших невязок и методом скорейшего спуска
Задаем матрицу коэффициентов и столбец свободных членов
Вводим начальное приближение решения
Устанавливаем значение погрешности расчета
Метод Якоби для решения СЛАУ Вводим функцию, реализующую алгоритм метода Якоби: Вызываем данную функцию
Выводим решение СЛАУ и количество итераций
Выводим значение вектора невязки
Метод Зейделя для решения СЛАУ Вводим функцию, реализующую алгоритм метода Зейделя:
Вызываем данную функцию
Выводим решение СЛАУ и количество итераций
Выводим значение вектора невязки
Метод минимальных невязок для решения СЛАУ Вводим функцию, реализующую алгоритм метода минимальных невязок:
Вызываем данную функцию
Выводим решение СЛАУ и количество итераций
Выводим значение вектора невязки
Метод скорейшего спуска для решения СЛАУ
Вводим функцию, реализующую алгоритм метода скорейшего спуска:
Вызываем данную функцию
Выводим решение СЛАУ и количество итераций
Выводим значение вектора невязки
Варианты заданий к лабораторной работе №4 Решите системы уравнений итерационными методами 1) 3) 5)
7)
9)
Содержание отчета Отчет должен содержать: 1) титульный лист; 2) постановку задачи (согласно варианту);
3) краткое описание итерационных методов расчета СЛАУ; 4) программную реализацию данных методов; 5) выводы о проделанной работе. Контрольные вопросы и задания 1. Какие методы решения СЛАУ вы знаете? 2. Запишите каноническую форму одношаговых (двухслойных) итерационных схем. 3. От чего зависит скорость сходимости итерационных методов? 4. Какие преимущества у вариационно-итерационных методов? 5. Каким образом определяется окончание итераций? 6. Запишите метод Якоби в векторной форме. 7. Запишите метод Зейделя в векторной форме. 8. Запишите формулу расчета итерационного параметра согласно методу скорейшего спуска. 9*. Условие применимости метода минимальных невязок. 10*. Условие применимости метода скорейшего спуска. Методы решения задачи Коши
Метод Эйлера. Пусть требуется решить задачу Коши: найти функцию
Решение задачи (5.1) существует и единственно, если функции Ставится задача нахождения приближенных значений функции Одним из простейших методов численного решения задачи Коши (5.1) является метод Эйлера, основанный на использовании разностной схемы Эйлера:
Разностная схема (5.2) называется явной, так как значения
В результате получаем приближенные значения функции
называется погрешностью разностной схемы. Подставляя
где
Невязка Оценим величину
Учитывая, что Таким образом, разностная схема (5.2) имеет первый порядок аппроксимации.
Докажем сходимость разностной схемы Эйлера (5.2), т.е. что
В этом случае разностная схема (5.2) называется сходящейся и имеющей первый порядок точности. Таким образом, метод Эйлера достаточно прост, но обеспечивает низкую точность. Метод Рунге–Кутта Повышение порядка точности осуществляется путем усложнения разностной схемы. На практике широко распространенными являются разностные схемы Рунге–Кутта второго и четвертого порядка точности.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.230 (0.047 с.) |
 , т.е.
, т.е.  и
и  , входящие в оценку
, входящие в оценку  и необходимые для выбора
и необходимые для выбора  , здесь не требуются. Рассмотрим методы минимальных невязок и скорейшего спуска.
, здесь не требуются. Рассмотрим методы минимальных невязок и скорейшего спуска.
 получим равенство, умножив обе части равенства (4.13) на матрицу
получим равенство, умножив обе части равенства (4.13) на матрицу  .
. или
или
 будем выбирать из условия минимума невязки
будем выбирать из условия минимума невязки  по норме
по норме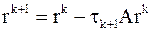 .
.
 по
по  ,
,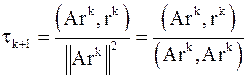 .
.
 где
где  ,
,  – точное решение исходной системы. Поскольку
– точное решение исходной системы. Поскольку  , и учитывая, что
, и учитывая, что , получим
, получим
 по
по  , откуда
, откуда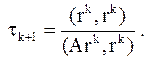

 ,
,  .
. .
. .
.

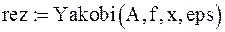 .
. ,
, 
 .
. .
.
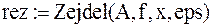 .
.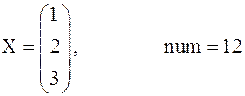 .
. .
.
 .
. .
. .
.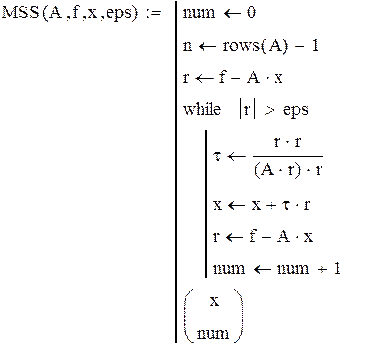
 .
. .
. .
. 2)
2) 
 4)
4) 
 6)
6) 
 8)
8) 
 10)
10) 
 , непрерывную при
, непрерывную при  , удовлетворяющую при
, удовлетворяющую при 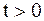 дифференциальному уравнению и начальному условию при
дифференциальному уравнению и начальному условию при  :
: .
.
 и
и  непрерывны в области
непрерывны в области  , содержащей точку
, содержащей точку  .
.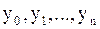 в точках
в точках  соответственно отрезка
соответственно отрезка  . Совокупность точек
. Совокупность точек  называется сеткой; точки
называется сеткой; точки  – узлами сетки,
– узлами сетки,  – шагом сетки.
– шагом сетки. .
. находятся последовательно, начиная с
находятся последовательно, начиная с  по явной формуле
по явной формуле ,
,  ,
,  , т.е. сеточную функцию
, т.е. сеточную функцию  ,
, 
 из (5.3) в уравнение (5.2), имеем
из (5.3) в уравнение (5.2), имеем ,
,
 ,
,  .
. , которую имеет разностная схема (5.2) на решении задачи (5.1), называется погрешностью аппроксимации разностной схемы (5.2).
, которую имеет разностная схема (5.2) на решении задачи (5.1), называется погрешностью аппроксимации разностной схемы (5.2). . Для этого, разлагая по формуле Тейлора функцию
. Для этого, разлагая по формуле Тейлора функцию  в окрестности точки
в окрестности точки 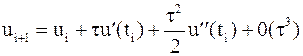 .
.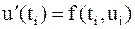 , имеем
, имеем  или
или  .
. . Действительно, определяя величину
. Действительно, определяя величину 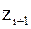 из (5.4) и оценивая ее, имеем
из (5.4) и оценивая ее, имеем



