
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение потерь напора при движении жидкости
При решении гидравлических задач, связанных с движением жидкости, для определения того или другого параметра движущейся жидкости необходимо предварительно определить потери напора, которые учитываются в четвертом члене уравнения Бернулли (1). Потери напора обычно считают состоящими из двух видов: потери напора по длине трубопровода hтp, обусловленные затратами энергии на преодоление сил внутреннего трения в жидкости, и потери напора в местных сопротивлениях hм, обусловленные затратами энергии жидкости не только на преодоление сил внутреннего трения, но и на перемешивание жидкости
Потери напора на трение по длине трубы при любом режиме движения определяются по формуле Дарси:
При ламинарном движении жидкости λ=64/Re и формула (5) становится формулой Пуазейля:
где hтр - потери напора; ∆Ртр- потери, выраженные через величину давления; λ - коэффициент гидравлического трения; l - длина расчетного участка трубы; d - диаметр трубопровода; υ - средняя скорость движения жидкости; ρ - плотность жидкости; g - ускорение силы тяжести; Re - число Рейнольдса.
Где ν - кинематический коэффициент вязкости жидкости. Потери напора по длине трубы при турбулентном движении определяются также по формуле Дарси (5), но здесь уже λ - коэффициент трения определяется по другим зависимостям, чем в ламинарном потоке. Таким образом, формулы (5, 6) универсальны - их можно применить для любых жидкостей, в любом интервале температур и при любом режиме движения. Коэффициент λ при ламинарном движении зависит от числа Рейнольдса
а при турбулентном движении - от числа Рейнольдса Re и относительной шероховатости ∆э/d (или d/∆э), т.е.
где ∆э - эквивалентная шероховатость трубы; d - диаметр трубы. Имеется рад эмпирических формул для расчета коэффициента λ в зависимости от режима движения. Однако пользоваться этими формулами не всегда удобно. Для облегчения расчета здесь приводится опытный график Никурадзе (рисунок 1), из которого λ определяется весьма просто: по известным Re и ∆э/d (d/∆э). Величина местных гидравлических потерь определяется по формуле Вейсбаха
где hм - местные потери напора; ∆Pм - местные потери, выраженные через величину давления;
ξ - безразмерный коэффициент местного сопротивления; υ - средняя скорость в сечении, как правило, за местным сопротивлением. Значения коэффициентов местных сопротивлений зависят от конфигурации местного сопротивления, а так же от режима потока, подходящего к сопротивлению. Теоретическое определение коэффициента λ представляет значительные трудности ввиду большой сложности происходящих явлений, поэтому он определяется опытным путем. Значения некоторых из них приводятся в таблицах 1 и 2. Пользоваться приведенными здесь значениями коэффициентов местных сопротивлений можно лишь в тех случаях, когда расстояние между отдельными сопротивлениями не меньше 20..30 диаметров трубопровода. В противном случае сопротивления работают как одна система, для которой необходимо определить свое значение коэффициента местного сопротивления экспериментальным путем.
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.87 (0.004 с.) |

 или
или  (5)
(5) или
или  (5)
(5) , (7)
, (7) , (8)
, (8)
 , (9)
, (9)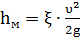 или
или  , (10)
, (10)


