
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кванты – переносчики взаимодействия
В классической электродинамике взаимодействие между зарядами осуществляется через поле, каждый заряд создает поле и это поле действует на другие заряды. В квантовой теории поле представляется как поток фотонов, взаимодействие между зарядом и полем выглядит как поглощение и испускание кванта поля – фотона. Зададимся вопросом: как возможно испускание фотонов, если частица при этом теряет энергию и может быть нарушен закон сохранения энергии. Чтобы объяснить возможность обмена фотонами с энергетической точки зрения, следует учесть принцип неопределенности Гейзенберга. Отношение неопределенности связывает энергию частицы со временем ее существования: Понятие вакуумного состояния. Минимальная энергия поля В квантовой механике поле представляется как поле фотонов, которое имеет запас энергии и может отдавать ее порциями. Уменьшение энергии поля на величину С точки зрения квантовой теории поля, электромагнитное поле не перестает существовать, а находится в состоянии с минимальной энергией. Поскольку в данном состоянии фотонов нет, его естественно называть вакуумным состоянием электромагнитного поля или фотонным вакуумом. Вакуум – низшее энергетическое состояние поля, но согласно принципу неопределенности, нельзя считать энергию поля нулевой. Физический вакуум не «пустота», а особое состояние, которое проявляет определенные физические свойства. Если полю в вакуумном состоянии сообщить достаточную энергию, то происходит его возбуждение, т. е. рождение частицы – кванта поля. Квантование поля Метод квантования полей был разработан в 1927 г. П.А.М.Дираком, предложившим ввести операторы, описывающие рождение и уничтожение частиц. Чтобы пояснить суть метода Дирака, рассмотрим систему операторов, состоящую из одинаковых частиц в одном и том же состоянии. В квантовой механике состояние системы частиц описывается волновой функцией или вектором состояния. Если через N обозначить число частиц, то
Введем операторы уничтожения частицы а– и оператор рождения частицы а+. По определению а– переводит состояние с N частицами в состояние с N – 1 частицей:
а+ переводит состояние с N частицами в состояние с N + 1 частицей:
В частности, если имеется вакуумное состояние поля где N=0,
Характерным свойством операторов рождения и уничтожения частиц является то, что они не коммутируют.
Операторы рождения и уничтожения частиц удовлетворяют перестановочному отношению
Приведенные выше перестановочные отношения выполняются для полей, кванты которых имеют целый спин, т.е. являются бозонами и могут находиться в одном состоянии. Если описывается система фермионов, то согласно принципу запрета Паули, все частицы должны находиться в различных состояниях. Соответственно операторы рождения и уничтожения частиц следует конкретизировать, добавив указание к какому состоянию частицы эти операторы относятся. С учетом различных состояний частиц перестановочные отношения запишутся в виде
Перестановочные отношения отражают тот факт, что невозможно уничтожить частицы, которых нет, то есть
Квантовая электродинамика (КЭД) Квантовая электродинамика является теорией электромагнитного взаимодействия и представляет собой часть теории поля. В квантовой электродинамике рассматриваются процессы взаимодействия заряженных частиц с электромагнитным полем.. Основные электродинамические явления могут быть сведены к трем процессам: фотон взаимодействует с фотоном, фотон взаимодействует с электроном, электрон взаимодействует с электроном. Диаграммы Фейнмана
Согласно теории относительности длина стрелок находится по формулам для 4-х интервала. С величиной интервала данной стрелки в КЭД связывается амплитуда – плотность вероятности того, что частица, которая находится в данный момент времени в данном месте, окажется в другой момент времени в другом месте. Поэтому диаграммы Фейнмана не только являются иллюстрацией реакций с частицами, но и позволяют сделать оценки соотношения вероятностей процессов. В частности, с их помощью легко доказать доминирующую роль низших по числу вершин (или количеству виртуальных частиц) диаграмм в электромагнитных взаимодействиях.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.158 (0.007 с.) |
 Если рассматривается взаимодействие посредством обмена фотоном, то за
Если рассматривается взаимодействие посредством обмена фотоном, то за  принимается продолжительность одного акта обмена. Энергия частицы не является точно определенной, поэтому законы сохранения энергии и импульса не препятствуют испусканию и поглощению квантов взаимодействия, если только эти кванты существуют в течении времени
принимается продолжительность одного акта обмена. Энергия частицы не является точно определенной, поэтому законы сохранения энергии и импульса не препятствуют испусканию и поглощению квантов взаимодействия, если только эти кванты существуют в течении времени 
 означает исчезновение одного фотона частоты
означает исчезновение одного фотона частоты 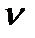 , т.е. переход поля в состояние с уменьшением числа фотонов на единицу. Если процесс исчезновения фотонов будет продолжаться, то образуется состояние, в котором число фотонов равно нулю и дальнейшая отдача энергии не возможна.
, т.е. переход поля в состояние с уменьшением числа фотонов на единицу. Если процесс исчезновения фотонов будет продолжаться, то образуется состояние, в котором число фотонов равно нулю и дальнейшая отдача энергии не возможна. определяет вероятность данного состояния. Если число частиц N точно известно, то
определяет вероятность данного состояния. Если число частиц N точно известно, то  , т.е. вектор состояния для любого фиксированного N нормирован на единицу.
, т.е. вектор состояния для любого фиксированного N нормирован на единицу. .
. .
. ,где
,где  – вектор состояния, характеризующий вакуум. Таким образом, получается одночастичное состояние, которое получается в результате рождения из вакуума одной частицы. Определение вакуума
– вектор состояния, характеризующий вакуум. Таким образом, получается одночастичное состояние, которое получается в результате рождения из вакуума одной частицы. Определение вакуума  , т.к. невозможно уничтожить частицу в состоянии в котором частиц нет. Вакуумный вектор состояние
, т.к. невозможно уничтожить частицу в состоянии в котором частиц нет. Вакуумный вектор состояние  имеет в квантовой теории поля особое значение, так как из него при помощи оператора а+, можно получить любые состояния, применив его соответствующее количество раз.
имеет в квантовой теории поля особое значение, так как из него при помощи оператора а+, можно получить любые состояния, применив его соответствующее количество раз. .
.

 где n, m – целые числа, обозначающие номера частиц.
где n, m – целые числа, обозначающие номера частиц. . Данные соотношения имеют место для полей, кванты которых имеют полуцелый спин и подчиняются принципу запрета Паули, запрещающего наличие в одной системе двух систем в одинаковых состояниях.
. Данные соотношения имеют место для полей, кванты которых имеют полуцелый спин и подчиняются принципу запрета Паули, запрещающего наличие в одной системе двух систем в одинаковых состояниях. Для описания этих процессов используются диаграммы Фейнмана, которые представляют собой графики движения частиц в 4-х мерном пространстве-времени. В диаграммах Фейнмана физическому процессу сопоставляется его графическая схема. Движение фотона отображается волнистой линией движение электрона – прямой, движение античастиц изображается как движение вспять по времени. Взаимодействие частиц на диаграмме изображается вершиной (или узлом), в котором сходятся две фермионных и одна бозонная линии (см. рис. 5.9). Линии, один из концов которых свободен, соответствуют свободным частицам. Данный рисунок иллюстрирует процесс испускания фотона электроном.
Для описания этих процессов используются диаграммы Фейнмана, которые представляют собой графики движения частиц в 4-х мерном пространстве-времени. В диаграммах Фейнмана физическому процессу сопоставляется его графическая схема. Движение фотона отображается волнистой линией движение электрона – прямой, движение античастиц изображается как движение вспять по времени. Взаимодействие частиц на диаграмме изображается вершиной (или узлом), в котором сходятся две фермионных и одна бозонная линии (см. рис. 5.9). Линии, один из концов которых свободен, соответствуют свободным частицам. Данный рисунок иллюстрирует процесс испускания фотона электроном.


