
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стационарное уравнение Шредингера
Требуется найти оператор энергии для частицы, которая движется вдоль оси х со скоростью vx и энергией E в поле с потенциальной энергией V. Полная энергия частицы H равна сумме ее кинетической и потенциальной V (x) энергий: H = Воспользуемся тем, что импульс px = m vx и выразим кинетическую энергию через импульс: H = Учитывая, что оператор импульса px ≡ H ≡ Чтобы найти собственные значения этого оператора надо решить уравнение для собственных значений.
Удовлетворяющие данному уравнению значения E являются собственными числами оператора энергии, то есть совпадают со всевозможными допустимыми значениями энергии материальной точки. Если мы перенесем все в левую часть, то получим частный вид уравнения Шредингера:
Это стационарное уравнение Шредингера, решение которого зависит от вида потенциала V (x). Если предположить, что частица движется свободно, то есть, что потенциальная энергия V(x)=0, можно найти частный вид решения этого уравнения: ψ(х) = х Видно, что решение этого уравнения — мнимая величина, но физическая величина должна быть вещественной. Мнимая величина не имеет физического смысла. Какой смысл имеет ψ – функция (волновая функция) до сих пор остается открытым вопросом. Проблема интерпретации этого результата называется проблемой ψ – функции. Физическую интерпретацию получил лишь квадрат ψ – функции: |ψ|2 = ψ* ψ. Он имеет смысл плотности вероятности обнаружить частицу в данной области пространства. Амплитуда вероятности Обычная вероятность описывает некоторую систему, которая может находиться в различных альтернативных состояниях. Вероятность – это действительное число, которое изменяется в пределах от нуля до единицы 0 ≤ p ≤ 1. Понятие вероятности в квантовой механике аналогично классическому, с той лишь разницей, что р – комплексное число.
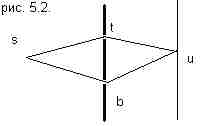
Вернемся к эксперименту с двумя щелями (рис. 5.2.). Какова классическая вероятность найти электрон в точке u? Если открыта только верхняя щель, она равна произведению вероятностей того, что электрон попадет из точки s в точку t, а из точки t в точку u. P(s,t)× P(t,u) Если открыта только нижняя щель, она равна произведению вероятностей того, что электрон попадет из точки s в точку b, а из точки b в точку u.
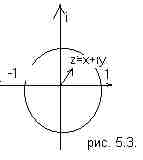
P(s,b)× P(b,u) Если открыты обе щели, то полная вероятность равна сумме этих двух вероятностей P(s,u) = P(s,t)× P(t,u)+ P(s,b)× P(b,u) В квантовой механике правила вычислений будут аналогичными, но вместо вероятности будет стоять амплитуда вероятности. A(s,u) = A(s,t)× A(t,u)+ A(s,b)× A(b,u) Как можно интерпретировать амплитуду вероятности? Комплексное число z=x+iy можно представить, в виде вектора с началом в точке O и концом в точке (x,y) на комплексной плоскости (см. рис. 5.3.) Для получения классической вероятности надо взять квадрат модуля амплитуды |z|2 = x2+y2, который является вещественным числом и, если необходимо, нормировать. Если открыта только одна щель, то амплитуда того, что электрон попадет на экран, равна произведению амплитуд, что он из точки s попадет в точку t, а из точки t попадет в точку u: А(s, t)*А(t, u). Если открыта другая щель, то амплитуда будет равна А(s, b)*А(b, u). Квадрат модуля произведения равен произведению квадратов |zw|2 = |z|2|w|2, Если открыт более чем один маршрут, надо образовать суммы. Сумма комплексных чисел зависит от угла между ними |w+z|2 = |w|2+|z|2+2|z||w|cos θ, где –1<cos θ<1. В тех областях экрана, где фазы колебаний совпадают, cos θ = 1 и волны усиливают друг друга. Освещенность в таких местах экрана возрастает в 4 раза. Там где волны находятся в противофазе cos θ = –1 и волны гасятся, образуя темную полосу нулевой освещенности. В промежуточных положениях освещенность убывает пропорционально разности амплитуд. Волновой пакет Если бы элементарная частица была точечной, то вероятность ее нахождения в некоторой точке пространства, была бы равна нулю, если частицы там нет, или единице, если частица там есть. Но элементарные частицы не точки и, строго говоря, их нельзя считать локализоваными в бесконечно малой области пространства. Свободно движущийся электрон представляет собой волновой пакет, т. е. «сгусток» распространяющихся вместе электронных волн. Ширина волнового пакета не остается постоянной во времени, а непрерывно увеличивается. В квантовой механике каждому состоянию частицы с определенным значением импульса и энергии соответствует волна де Бройля, т.е. волна с определенным значением частоты и длины волны, занимающая все пространство. Если частица имеет энергию Е и импульс р, то с ней связана волна, частота которой
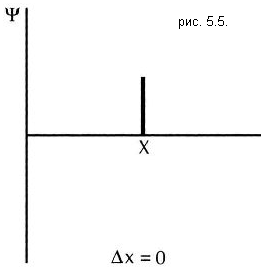
Координата частицы с точно определенным импульсом является полностью неопределенной – частица с равной вероятностью может быть обнаружена в любой точке пространства, что соответствует соотношению неопределенностей. Если же частица локализована в некоторой ограниченной области пространства, то ее импульс уже не является точно определенной величиной (см. рис. 5.5. и рис. 5.6.).
Состояние каждой частицы представляется как сумма волн с частотами, соответствующими интервалу возможных значений импульса. Наложение (суперпозиция) группы таких волн, имеющих почти одинаковое направление распространения, но слегка отличающихся по частотам и образует волновой пакет: результирующая волна будет отлична от нуля лишь в некоторой ограниченной области пространства. То есть вероятность обнаружить частицу в этой области велика, а вне ее практически равна нулю. Скорость волнового пакета совпадает с механической скоростью частицы. Из того, что электрон представляет собой волновой пакет, не локализованный в одной точке пространства, следует невозможность различить электроны. Тождественность электронов Электроны являются элементарными частицами, каждая из которых обладает одинаковыми физическими свойствами: определенной массой me, зарядом –е, спином es=±1/2 и пропорциональным спину магнитным моментом. Следовательно, электроны при одинаковых внешних условиях движутся одинаково. В классической механике для того, чтобы различать частицы достаточно пометить их в некоторый начальный момент времени. В квантовой механике частицы представлены волновыми пакетами. Допустим мы пометим номерами два волновых пакета. С течением времени они расплываются в пространстве. Если взять точку из области наложения этих расплывшихся волновых пакетов, то можно ли сказать какой из электронов наблюдается? В квантовой механике имеется лишь возможность вычислить вероятность нахождения частицы в той или иной точке пространства. Поэтому волновая функция только определяет область, в которой возможно движение частицы. Если для двух или более частиц области допустимых значений перекрываются, то нельзя определить, какая именно частица обнаружена в данной точке. Следовательно, частицы следует рассматривать как тождественные. Из принципа тождественности частиц следует невозможность различить два состояния системы, которые отличаются друг от друга только перестановкой двух частиц одинаковой природы. Важное следствие принципа тождественности частиц состоит в том, что вол Принцип тождественности математически означает, что распределение плотностей вероятности найти частицу совпадают при замене одного электрона на другой. |Ψ(1,2)|2=|Ψ(2,1)|2. Это возможно если функции пропорциональны Ψ(1,2)=k2 Ψ(2,1), где k2=1, k=±1. Следовательно, перестановка двух одинаковых частиц не повлечет за собой изменения состояния системы тогда и только тогда, когда волновая функция системы является
1) симметричной Ψ(1,2)= Ψ(2,1), 2) антисимметричной Ψ(1,2)= –Ψ(2,1). В общем случае Ψ функция не будет ни симметричной, ни антисимметричной, но из взаимозаменяемости частиц следует, что для системы из частиц одинаковой природы всегда существуют волновые функции, одни симметричные, другие антисимметричные по отношению ко всем парам частиц одинаковой природы. Состояние, волновая функция которого симметрична, называется симметричным состоянием системы, а состояние, волновая функция которого антисимметрична, – антисимметричным состоянием системы. Симметричная зависимость от координат каждой пары частиц означает невозможность осуществить переход системы из симметричного состояния в ассиметричное и обратно. То есть, симметричное и ассиметричное состояния образуют два отдельных ансамбля, между которыми невозможны никакие переходы. То есть для частиц одного типа может осуществляться либо симметричное, либо антисимметричное состояние, поскольку если ансамбль находится в начальный момент времени в состоянии одного типа, то он навсегда останется в этом состоянии. Принцип Паули Волновые функции системы тождественных частиц, обладающих полуцелыми спинами (электроны, протоны, нейтроны) являются антисимметричными. Волновые функции системы тождественных частиц с целыми спинами (фотоны, π-мезоны) являются симметричными. Частицы с полуцелыми спинами носят название фермионов, а частицы с целыми спинами – название бозонов. Частицы с полуцелыми спинами – электроны, протоны, нейтроны и др. являются частицами, из которых состоит вещество, частицы с целыми спинами, например, фотон, являются переносчиками взаимодействия. В соответствии со свойствами симметрии волновых функций при описании состояний частиц говорят о статистике Ферми-Дирака (для фермионов) или о статистике Бозе-Эйнштейна (для бозонов). Принцип Паули формулируется для фермионов, этот принцип не является логически необходимым следствием квантовой механики, поэтому кратко рассмотрим причину его формулировки. При изучении строения атома было отмечено, что существует насыщение энергетических уровней, то есть на каждом энергетическом уровне может находиться не больше определенного числа электронов. Чтобы объяснить этот факт, Паули предположил, что два электрона не могут находиться в строго тождественных состояниях. Таким образом, для частного случая квантовых систем – атомов или молекул – принцип Паули формулируется следующим образом: в атоме или молекуле два электрона никогда не находятся в одном и том же квантовом состоянии. То есть, если существование электрона в некотором квантовом состоянии запрещает появление еще одного электрона в этом же состоянии.
Принцип Паули действует только для фермионов. Для бозонов, волновая функция которых симметрична, одинаковые частицы симметричны в отношении занимаемых ими положений и "не мешают" друг другу занимать одинаковые физические состояния. Следовательно, бозоны могут находиться в одинаковых квантовых состояниях. Значение принципа Паули в том, что он дал возможность объяснить насыщение энергетических уровней. Теперь чтобы узнать максимальное число электронов на данном уровне нужно посчитать число возможных состояний, которые соответствуют различным комбинациям квантовых чисел. Для описания состояния элементарных частиц, используют понятие квантового числа. Например, если электроны находятся в разных состояниях, то все наборы квантовых чисел, характеризующих состояние электрона в атоме, должны быть различными. Рассмотрим понятие квантового числа более подробно.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.6.194 (0.018 с.) |
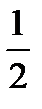 m vx2+ V (x).
m vx2+ V (x). +V(x).
+V(x).
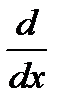 получим
получим
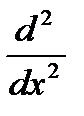 +V(x). (оператор энергии)
+V(x). (оператор энергии)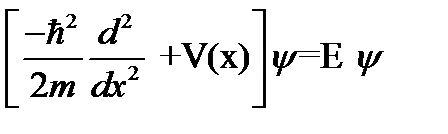 .
.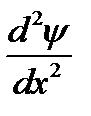 +
+  [ E — V (x)] ψ = 0.
[ E — V (x)] ψ = 0.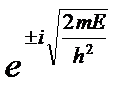 .
.
 .
.
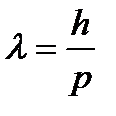
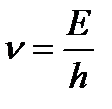 и длина волны
и длина волны 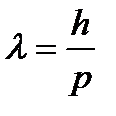 .
.

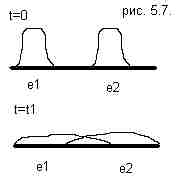 новая функция системы частиц при перестановке координат двух частиц не должна меняться.
новая функция системы частиц при перестановке координат двух частиц не должна меняться.


