
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
История появления понятия «кванта»Стр 1 из 5Следующая ⇒
Квантовые теории Введение Всего в природе известно четыре вида фундаментальных взаимодействий. ОТО описывает одно из этих взаимодействий – гравитационное. Три других вида взаимодействий – электромагнитное, слабое и сильное – описываются квантовыми теориями. Квантовая теория гравитации находится в стадии разработки. В рамках данного курса мы кратко затронем квантовые теории, играющие фундаментальную роль в современной физике: квантовую механику, квантовую теорию поля и такие ее разделы как квантовая электродинамика, квантовая хромодинамика и теории слабого взаимодействия. Классическая картина мира в начале XX в. основывалась на представлениях о двух типах физических объектах: частиц и полей. Квантовая механика рассматривает объекты микромира как частицы, а квантовая теория поля – как кванты полей. Такие теории, как квантовая электродинамика, квантовая хромодинамика и теория электрослабого взаимодействия, описывающие, соответственно, электромагнитное, сильное и слабое взаимодействие, представляют собой воплощение идей квантовой теории поля. Квантовая механика должна объяснять как корпускулярные, так и волновые свойства вещества ирассматривает элементарные частицы как волновые пакеты. Квантовая или волновая механика описывает законы движения микрочастиц, связывая характеристики как частиц (энергия, импульс), так и волн (частота, длина волны). Квантовая механика применима лишь для описания систем с неизменным числом частиц, но не для описания их рождения или уничтожения. Задачи об испускании и поглощении частиц описываются квантовой теорией поля. Квантовая теория поля рассматривает второй элемент классической картины мира – поля. Эта теория является релятивистской квантовой теорией физических систем с бесконечным числом степеней свободы. Эта теория построена для описания одного из самых общих свойств микромира – взаимной превращаемости элементарных частиц. Для описания такого рода процессов требовался переход к квантовому волновому полю. Квантовая теория поля с необходимостью является релятивистской, поскольку если система состоит из медленно движущихся частиц, то их энергия может оказаться недостаточной для образования новых частиц с ненулевой массой покоя. Квантовая теория поля описывает три типа фундаментальных взаимодействий и, соответственно, состоит из трех частей: квантовой электродинамики, квантовой хромодинамики и теории электрослабого взаимодействия.
Квантовая электродинамика, (авторы С. Томонога, Ю.С. Швингер, Р.Ф. Фейнман) сформировавшаяся к началу 1950 г., является теорией электромагнитного взаимодействия и входит в состав теории поля. Квантовая электродинамика – та часть квантовой теории поля, в которой рассматривается взаимодействие электромагнитного поля и заряженных частиц (или электронно-позитронного поля). Квантовая электродинамика описывает взаимодействие квантованных электромагнитных полей, заряженных частиц друг с другом, а также взаимодействие излучения с веществом. Электромагнитное взаимодействие рассматривается как обмен квантами электромагнитного поля – фотонами, любая заряженная частица создает поле, непрерывно излучая и поглощая виртуальные фотоны. Квантовая хромодинамика является теорией сильного взаимодействия, которое описывает взаимодействия между нуклонами (протонами и нейронами) в атомном ядре, а также между частицами, из которых состоят протоны, нейроны и другие адроны – кварками. Кварки могут быть разных типов (ароматов), их состояние описывается посредством 3-х зарядов (цветов). Сильное взаимодействие осуществляется посредством частиц-переносчиков сильного взаимодействия глюонов, обладающих единичным спином и нулевой массой покоя. Теория электрослабого взаимодействия Слабое взаимодействие – один из четырех видов взаимодействий, оно слабее сильного и электромагнитного, но гораздо сильнее гравитационного на малых расстояниях. Первым обнаруженным процессом, протекающим с участием слабого взаимодействия является b-распад. В слабом взаимодействии участвуют и тяжелые частицы – адроны и легкие частицы – лептоны. Оно является единственным типом взаимодействий, в которых участвуют нейтрино. Единая теория электромагнитного и слабого взаимодействия была предложена в 1967-1968 гг. А. Саламом и С. Вайнбергом. Прежде чем перейти к более подробному обсуждению упомянутых теорий, рассмотрим появление понятия кванта.
Понятие кванта Макс Планк, пытаясь найти формулу, согласующуюся с экспериментальными значениями во всем диапазоне частот, предположил, что излучаемая энергия изменяется дискретными порциями – квантами. Физический смысл кванта – минимальное значение переносимой энергии, таким образом, нагретое тело может излучать только те волны, которые могут переносить энергию не меньше, чем некоторая минимальная порция. Планк предположил, что энергия осциллятора пропорциональна его частоте ε0=h ν. Входящая в выражение константа h = 6,625·10-34 Дж·с называется постоянной Планка. Часто она используется в виде ħ = h /2 π = 1,05·10-34 Дж·с и тогда формула Планка перепишется в виде ε0= ħω. В формуле Планка энергия изменяется порциями, кратными величине h. Если энергия волны может быть представлена как сумма n элементарных волн, то энергия электромагнитной волны равна εn= nhν, а энергия всего электромагнитного поля – сумме энергий волн E = Но формула Планка предполагала, что энергия излучается только дискретными порциями – квантами, что противоречило общепринятому пониманию энергии, как непрерывной величины. Сам Планк не давал никакой физической интерпретации своей постоянной ħ и рассматривал введение ее как вынужденный технический прием, чтобы данные экспериментов соответствовали расчетам. Физическая интерпретация понятия кванта позже была дана Эйнштейном, во время исследования проблемы фотоэффекта. Фотоэффект В 1887 году Г. Герц обнаружил, что когда на поверхность металла падает свет, металл испускает электроны. Само явление фотоэффекта не казалось парадоксальным: было известно, что электроны в металлах слабо связаны с ядрами и свет, падающий на металл, вполне мог сообщить энергию, достаточную, чтобы выбить с поверхности электроны. Необычными казались свойства фотоэффекта. При освещении металла светом постоянной частоты и фазы (когерентным), все выбиваемые электроны обладали одинаковой энергией. Казалось бы, что при увеличении интенсивности излучения (яркости света) скорость вылетающих электронов увеличится, так как электромагнитное поле переносит больше энергии. Но с ростом интенсивности света, увеличивалось только число вылетевших электронов, а их скорость не менялась. С уменьшением частоты света выбиваемые электроны уменьшали свою энергию, пока не наступал момент, когда скорость падала до нуля и они переставали вылетать с поверхности, независимо от интенсивности источника света. Волновая теория не могла объяснить фотоэффект, объяснение было дано Эйнштейном, применившим введенное Планком понятия кванта – дискретной порции энергии. Эйнштейн предположил, что не только энергия должна рассматриваться как дискретная, но и световой луч должен рассматриваться как поток микроскопических частиц – фотонов. Он ввел импульс светового кванта по формуле p = hk, где k =
Квантовая механика Амплитуда вероятности Обычная вероятность описывает некоторую систему, которая может находиться в различных альтернативных состояниях. Вероятность – это действительное число, которое изменяется в пределах от нуля до единицы 0 ≤ p ≤ 1. Понятие вероятности в квантовой механике аналогично классическому, с той лишь разницей, что р – комплексное число.
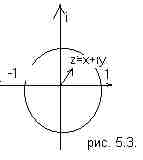
Вернемся к эксперименту с двумя щелями (рис. 5.2.). Какова классическая вероятность найти электрон в точке u? Если открыта только верхняя щель, она равна произведению вероятностей того, что электрон попадет из точки s в точку t, а из точки t в точку u. P(s,t)× P(t,u) Если открыта только нижняя щель, она равна произведению вероятностей того, что электрон попадет из точки s в точку b, а из точки b в точку u. P(s,b)× P(b,u) Если открыты обе щели, то полная вероятность равна сумме этих двух вероятностей P(s,u) = P(s,t)× P(t,u)+ P(s,b)× P(b,u) В квантовой механике правила вычислений будут аналогичными, но вместо вероятности будет стоять амплитуда вероятности. A(s,u) = A(s,t)× A(t,u)+ A(s,b)× A(b,u) Как можно интерпретировать амплитуду вероятности? Комплексное число z=x+iy можно представить, в виде вектора с началом в точке O и концом в точке (x,y) на комплексной плоскости (см. рис. 5.3.) Для получения классической вероятности надо взять квадрат модуля амплитуды |z|2 = x2+y2, который является вещественным числом и, если необходимо, нормировать. Если открыта только одна щель, то амплитуда того, что электрон попадет на экран, равна произведению амплитуд, что он из точки s попадет в точку t, а из точки t попадет в точку u: А(s, t)*А(t, u). Если открыта другая щель, то амплитуда будет равна А(s, b)*А(b, u). Квадрат модуля произведения равен произведению квадратов |zw|2 = |z|2|w|2,
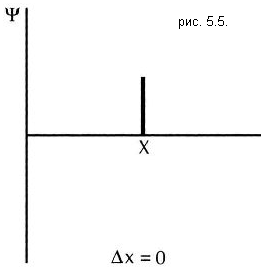
Если открыт более чем один маршрут, надо образовать суммы. Сумма комплексных чисел зависит от угла между ними |w+z|2 = |w|2+|z|2+2|z||w|cos θ, где –1<cos θ<1. В тех областях экрана, где фазы колебаний совпадают, cos θ = 1 и волны усиливают друг друга. Освещенность в таких местах экрана возрастает в 4 раза. Там где волны находятся в противофазе cos θ = –1 и волны гасятся, образуя темную полосу нулевой освещенности. В промежуточных положениях освещенность убывает пропорционально разности амплитуд. Волновой пакет Если бы элементарная частица была точечной, то вероятность ее нахождения в некоторой точке пространства, была бы равна нулю, если частицы там нет, или единице, если частица там есть. Но элементарные частицы не точки и, строго говоря, их нельзя считать локализоваными в бесконечно малой области пространства. Свободно движущийся электрон представляет собой волновой пакет, т. е. «сгусток» распространяющихся вместе электронных волн. Ширина волнового пакета не остается постоянной во времени, а непрерывно увеличивается. В квантовой механике каждому состоянию частицы с определенным значением импульса и энергии соответствует волна де Бройля, т.е. волна с определенным значением частоты и длины волны, занимающая все пространство. Если частица имеет энергию Е и импульс р, то с ней связана волна, частота которой Координата частицы с точно определенным импульсом является полностью неопределенной – частица с равной вероятностью может быть обнаружена в любой точке пространства, что соответствует соотношению неопределенностей. Если же частица локализована в некоторой ограниченной области пространства, то ее импульс уже не является точно определенной величиной (см. рис. 5.5. и рис. 5.6.).
Состояние каждой частицы представляется как сумма волн с частотами, соответствующими интервалу возможных значений импульса. Наложение (суперпозиция) группы таких волн, имеющих почти одинаковое направление распространения, но слегка отличающихся по частотам и образует волновой пакет: результирующая волна будет отлична от нуля лишь в некоторой ограниченной области пространства. То есть вероятность обнаружить частицу в этой области велика, а вне ее практически равна нулю. Скорость волнового пакета совпадает с механической скоростью частицы. Из того, что электрон представляет собой волновой пакет, не локализованный в одной точке пространства, следует невозможность различить электроны. Тождественность электронов Электроны являются элементарными частицами, каждая из которых обладает одинаковыми физическими свойствами: определенной массой me, зарядом –е, спином es=±1/2 и пропорциональным спину магнитным моментом. Следовательно, электроны при одинаковых внешних условиях движутся одинаково. В классической механике для того, чтобы различать частицы достаточно пометить их в некоторый начальный момент времени.
В квантовой механике частицы представлены волновыми пакетами. Допустим мы пометим номерами два волновых пакета. С течением времени они расплываются в пространстве. Если взять точку из области наложения этих расплывшихся волновых пакетов, то можно ли сказать какой из электронов наблюдается? В квантовой механике имеется лишь возможность вычислить вероятность нахождения частицы в той или иной точке пространства. Поэтому волновая функция только определяет область, в которой возможно движение частицы. Если для двух или более частиц области допустимых значений перекрываются, то нельзя определить, какая именно частица обнаружена в данной точке. Следовательно, частицы следует рассматривать как тождественные. Из принципа тождественности частиц следует невозможность различить два состояния системы, которые отличаются друг от друга только перестановкой двух частиц одинаковой природы. Важное следствие принципа тождественности частиц состоит в том, что вол Принцип тождественности математически означает, что распределение плотностей вероятности найти частицу совпадают при замене одного электрона на другой. |Ψ(1,2)|2=|Ψ(2,1)|2. Это возможно если функции пропорциональны Ψ(1,2)=k2 Ψ(2,1), где k2=1, k=±1. Следовательно, перестановка двух одинаковых частиц не повлечет за собой изменения состояния системы тогда и только тогда, когда волновая функция системы является 1) симметричной Ψ(1,2)= Ψ(2,1), 2) антисимметричной Ψ(1,2)= –Ψ(2,1). В общем случае Ψ функция не будет ни симметричной, ни антисимметричной, но из взаимозаменяемости частиц следует, что для системы из частиц одинаковой природы всегда существуют волновые функции, одни симметричные, другие антисимметричные по отношению ко всем парам частиц одинаковой природы. Состояние, волновая функция которого симметрична, называется симметричным состоянием системы, а состояние, волновая функция которого антисимметрична, – антисимметричным состоянием системы. Симметричная зависимость от координат каждой пары частиц означает невозможность осуществить переход системы из симметричного состояния в ассиметричное и обратно. То есть, симметричное и ассиметричное состояния образуют два отдельных ансамбля, между которыми невозможны никакие переходы. То есть для частиц одного типа может осуществляться либо симметричное, либо антисимметричное состояние, поскольку если ансамбль находится в начальный момент времени в состоянии одного типа, то он навсегда останется в этом состоянии. Принцип Паули Волновые функции системы тождественных частиц, обладающих полуцелыми спинами (электроны, протоны, нейтроны) являются антисимметричными. Волновые функции системы тождественных частиц с целыми спинами (фотоны, π-мезоны) являются симметричными. Частицы с полуцелыми спинами носят название фермионов, а частицы с целыми спинами – название бозонов. Частицы с полуцелыми спинами – электроны, протоны, нейтроны и др. являются частицами, из которых состоит вещество, частицы с целыми спинами, например, фотон, являются переносчиками взаимодействия. В соответствии со свойствами симметрии волновых функций при описании состояний частиц говорят о статистике Ферми-Дирака (для фермионов) или о статистике Бозе-Эйнштейна (для бозонов). Принцип Паули формулируется для фермионов, этот принцип не является логически необходимым следствием квантовой механики, поэтому кратко рассмотрим причину его формулировки. При изучении строения атома было отмечено, что существует насыщение энергетических уровней, то есть на каждом энергетическом уровне может находиться не больше определенного числа электронов. Чтобы объяснить этот факт, Паули предположил, что два электрона не могут находиться в строго тождественных состояниях. Таким образом, для частного случая квантовых систем – атомов или молекул – принцип Паули формулируется следующим образом: в атоме или молекуле два электрона никогда не находятся в одном и том же квантовом состоянии. То есть, если существование электрона в некотором квантовом состоянии запрещает появление еще одного электрона в этом же состоянии. Принцип Паули действует только для фермионов. Для бозонов, волновая функция которых симметрична, одинаковые частицы симметричны в отношении занимаемых ими положений и "не мешают" друг другу занимать одинаковые физические состояния. Следовательно, бозоны могут находиться в одинаковых квантовых состояниях. Значение принципа Паули в том, что он дал возможность объяснить насыщение энергетических уровней. Теперь чтобы узнать максимальное число электронов на данном уровне нужно посчитать число возможных состояний, которые соответствуют различным комбинациям квантовых чисел. Для описания состояния элементарных частиц, используют понятие квантового числа. Например, если электроны находятся в разных состояниях, то все наборы квантовых чисел, характеризующих состояние электрона в атоме, должны быть различными. Рассмотрим понятие квантового числа более подробно. Квантовая теория поля Квантовая механика позволяла описать многие атомные явления при помощи дискретного набора значений энергии, момента, но электромагнитное поле по-прежнему описывалось классическими уравнениями Максвелла, т.е. рассматривалось как непрерывное поле. В квантовой теории поля, в отличие от классической электродинамики, поле рассматривается, как состоящее из виртуальных частиц – квантов. Эта особенность обуславливает второе отличие полей от частиц: поле может порождаться и поглощаться, в то время как идея возникновения и уничтожения частиц чужда квантовой механике. В квантовой теории поля испускание и поглощение электромагнитных волн описывается как рождение и уничтожение фотона. Рождаться и исчезать могут не только фотоны, взаимопревращаемость частиц является универсальным свойством микромира. В результате столкновений при высоких энергиях одни частицы превращаются в другие. Квантовая механика является низкоэнергетическим приближением квантовой теории поля, когда энергии недостаточно для взаимопревращений частиц. Чтобы определить количество энергии, достаточной для превращения частиц, нужно воспользоваться отношением между массой и энергией, установленным в специальной теории относительности:
Энергия, необходимая для образования новой частицы не может быть меньше Квантование поля Метод квантования полей был разработан в 1927 г. П.А.М.Дираком, предложившим ввести операторы, описывающие рождение и уничтожение частиц. Чтобы пояснить суть метода Дирака, рассмотрим систему операторов, состоящую из одинаковых частиц в одном и том же состоянии. В квантовой механике состояние системы частиц описывается волновой функцией или вектором состояния. Если через N обозначить число частиц, то Введем операторы уничтожения частицы а– и оператор рождения частицы а+. По определению а– переводит состояние с N частицами в состояние с N – 1 частицей:
а+ переводит состояние с N частицами в состояние с N + 1 частицей:
В частности, если имеется вакуумное состояние поля где N=0,
Характерным свойством операторов рождения и уничтожения частиц является то, что они не коммутируют.
Операторы рождения и уничтожения частиц удовлетворяют перестановочному отношению
Приведенные выше перестановочные отношения выполняются для полей, кванты которых имеют целый спин, т.е. являются бозонами и могут находиться в одном состоянии. Если описывается система фермионов, то согласно принципу запрета Паули, все частицы должны находиться в различных состояниях. Соответственно операторы рождения и уничтожения частиц следует конкретизировать, добавив указание к какому состоянию частицы эти операторы относятся. С учетом различных состояний частиц перестановочные отношения запишутся в виде
Перестановочные отношения отражают тот факт, что невозможно уничтожить частицы, которых нет, то есть Квантовая электродинамика (КЭД) Квантовая электродинамика является теорией электромагнитного взаимодействия и представляет собой часть теории поля. В квантовой электродинамике рассматриваются процессы взаимодействия заряженных частиц с электромагнитным полем.. Основные электродинамические явления могут быть сведены к трем процессам: фотон взаимодействует с фотоном, фотон взаимодействует с электроном, электрон взаимодействует с электроном. Диаграммы Фейнмана
Согласно теории относительности длина стрелок находится по формулам для 4-х интервала. С величиной интервала данной стрелки в КЭД связывается амплитуда – плотность вероятности того, что частица, которая находится в данный момент времени в данном месте, окажется в другой момент времени в другом месте. Поэтому диаграммы Фейнмана не только являются иллюстрацией реакций с частицами, но и позволяют сделать оценки соотношения вероятностей процессов. В частности, с их помощью легко доказать доминирующую роль низших по числу вершин (или количеству виртуальных частиц) диаграмм в электромагнитных взаимодействиях. Рассеяние фотона на фотоне В классической электродинамике электромагнитные волны рассматриваются как невзаимодействующие. В квантовой теории поля могут образовываться виртуальные электрон-позитронные пары, т. е. свет может рассеиваться на свете. Диаграмма на рис. 5.12. соответствует процессу взаимодействия фотонов посредством образования промежуточной электрон-позитронной пары. В начальном состоянии имеется два фотона. Один из них в точке 1 исчезает, образовав электрон-позитронную пару. В точке 2 второй фотон поглощается позитроном. Затем появляются конечные фотоны: один из них рождается в точке 4 виртуальным электроном, а другой возникает в результате аннигиляции пары в точке 3.
Квантовая хромодинамика – это теория сильного взаимодействия, которое ответственно за силы действующие в атомных ядрах. Сильное взаимодействие является короткодействующим и осуществляется на малых расстояниях – 10–13 см. Квантовая хромодинамика изучает и позволяет объяснить основные свойства протонов, нейтонов и других частиц, называемых адронами. В основе квантовой хромодинамики лежит кварковая модель – представление, что все адроны состоят из кварков, которые и считаются по настоящему элементарными частицами. Впервые гипотеза существования кварков была выдвинута Гелл-Маном в 1964 г. Согласно этой модели адроны не являются элементарными частицами, а состоят из других частиц – кварков, которые удерживаются вместе с помощью частиц-переносчиков взаимодействия — глюонов (от английского glue – клей). Мезон состоят из пары кварк-антикварк, а барионы из трех кварков. Кварки находятся на расстоянии порядка 10–13 см. Кварки бывают различных типов (ароматов) и являются частицами с полуцелым спином, т.е. фермионами и, следовательно, их распределение должно подчиняться принципу запрета Паули. То есть в состав одной кварковой системы могут входить частицы с разными наборами квантовых чисел. Чтобы различать состояния кварков были введено квантовое число – ароматом кварка. Основные характеристики кварков
Нуклоны и π-мезоны состоят из u и d кварков, например, протон состоит из p = uud кварков, нейтрон n = udd; в состав странных частиц входит s кварк, очарованные частицы содержат c кварки, а ипсилон частицы содержат b кварки. Поскольку в состав частиц могут входить несколько кварков одного аромата, то чтобы удовлетворить принципу запрета Паули, было введено еще одно квантовое число – цвет. Кварк каждого «аромата» может обладать 3-мя цветовыми зарядами: «красным», «синим», «желтым». Противоположные заряды соответственно называются «антикрасным», «антисиним», «антижелтым». Суммарный цвет частицы должен быть «белым» или бесцветным. Взаимодействие кварков происходит за счёт обмена квантами цветового поля – глюонами, которые также несут различные цвета, но не чистые, а смешанные. Когда кварк испускает глюон, его цвет изменяется в зависимости от цвета глюона. Например, красный кварк, испуская красно-антисиний глюон, превращается в синий. Поляризация вакуума Любая частица в вакууме вызывает явление поляризации вакуума, основанное на рождении виртуальных пар. Аналогичное явление поляризации вакуума имеет место и в случае кварков. Кварк вызывает рождение пар глюонов, глюоны поляризуют глюонный вакуум, но это приводит не к экранировке как в случае электрического заряда, а к антиэкранировке цветового заряда. Цветовой заряд уменьшается внутри облака, то есть на бесконечно малых расстояниях между кварками цветовое взаимодействие выключается (ассимптотическая свобода). Увеличение расстояния приводит к росту сил взаимодействия с расстоянием, что не позволяет кваркам отдаляться друг от друга. Антиэкранировка цветового заряда приводит к тому, что кварк нельзя получить в свободном виде (проблема конфайнмента (confirment) —невылетания кварков из адронов). О существовании кварков можно судить на основе косвенных экспериментов, в которых исследуется внутренняя структура адронов. При рассеивании на адронах частиц высоких энергий на экране выделяются области повышенной плотности, которые и были интерпретированы как кварки. Однако ни кому не удавалось наблюдать свободный кварк. Кварки «пленены» в адронах и никогда не удаляются друг от друга больше, чем на расстояние 10–13 см. В то же время на более близких расстояниях они ведут себя как свободные частицы и это явление известно под названием «ассимптотическая свобода». Слабое взаимодействие Толчком для открытия слабого взаимодействия послужил процесс β-распада ядра, зарегистрированный в 1896 г. А. Беккерелем. При β-распаде нейтрон превращается в протон с образованием электрона и антинейтрино: n → p + e -+ Слабое взаимодействие – один из четырех видов фундаментальных взаимодействий, оно слабее сильного и электромагнитного, но гораздо сильнее гравитационного на коротких расстояниях. Об интенсивности взаимодействий можно судить по скорости процессов, которые оно вызывает. Обычно сравнивают между собой скорости процессов при значениях энергии около 1 ГэВ. При таких энергиях процесс обусловленный сильным взаимодействием происходит за время порядка 10–24 сек.; электромагнитным 10–21 сек.; слабым 10–10 сек. То есть в мире элементарных частиц процессы с участием слабого взаимодействия протекают сравнительно медленно. Слабое взаимодействие обладает очень малым радиусом действия – около 2*10–16 см. На расстояниях между ядрами двух соседних атомов в молекуле 10–8 см слабое взаимодействие чрезвычайно мало, оно гораздо слабее не только электромагнитного, но и гравитационного взаимодействия. На расстояниях <<2*10-16 см слабое и электромагнитное взаимодействие имеют практически одинаковую интенсивность. Это совпадение натолкнуло на мысль, что при высоких энергиях эти два взаимодействия представляют собой единое электрослабое взаимодействие. Теория электрослабого взаимодействия была разработана Саламом и Вайнбергом в 1967 г. Эта теория рассматривает переносчики электромагнитного взаимодействия – фотоны и переносчики слабого взаимодействия – Z, W бозоны как кванты единого калибровочного поля. Слабое взаимодействие играет очень важную роль в природе, оно ответственно за смену ароматов кварками и превращает заряженные лептоны в нейтрино. Именно благодаря слабому взаимодействию осуществляются ядерные реакции в звездах. Если бы не было слабого взаимодействия, были бы стабильны и распространены мюоны, π-мезоны, странные и очарованные частицы, которые распадаются в результате слабого взаимодействия. Слабое взаимодействие ответственно за все процессы, происходящие с участием нейтрино, нейтрино обладают только слабым и гравитационным взаимодействием. Слабое взаимодействие описывается теорией промежуточных векторных бозонов, которая постулирует существование переносчиков слабого взаимодействия – Z0, W+ и W–- бозонов. Первый из них – электрически нейтральный, а обмен двумя другими изменяет электрический заряд взаимодействующих частиц. СРТ-симметрия Сильное и электромагнитное взаимодействия инвариантны относительно некоторых преобразований. Такими преобразованиями являются одновременное отражение всех пространственных осей (Р) и обращения времени (Т). РТ-симметрия, означает инвариантность относительно зеркального отражение системы пространственных координат и обратного отсчета времени. Но слабое взаимодействие не сохраняет инвариантность относительно этих двух операций. Слабое взаимодействие инвариантно относительно СРТ – симметрии, то есть если кроме этих двух операций провести еще одну - операцию зарядового сопряжения (С): замены всех частиц на античастицы. Слабое взаимодействие не подчиняется ряду запретов, характерных для сильного и электромагнитного взаимодействия. Например, сильное и электромагнитное взаимодействие обладают зеркальной симметрией, которая заключается в том, что любые процессы, являющиеся зеркальным отражением друг друга протекают с одинаковой вероятностью. При слабом взаимодействии нарушается пространственная симметрия. Например, спин электронов при β-распаде направлен преимущественно против их импульса, то есть вероятность испускания электрона со спином, направленным по импульсу существенно меньше, чем противоположно импульсу М.Д.Ахундов, Л.Б.Баженов
ФИЛОСОФСКОЕ ПОНЯТИЕ МAТЕРИИ И РAЗВИТИЕ ФИЗИКИ ЭЛЕМЕНТAРНЫХ ЧAСТИЦ*
Проблема материи на протяжении тысячелетий стояла в центре внимания как
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.61.16 (0.075 с.) |
 . Формула εn= nhν давала для энергии значение, соответствующее экспериментальному.
. Формула εn= nhν давала для энергии значение, соответствующее экспериментальному.
 - волновой вектор, длина которого связана с длиной волны λ, частотой ω и скоростью света с. Эйнштейн предположил, что электромагнитное поле передает только определенную порцию (квант) энергии, которая переносится частицей света – фотоном. Электрон выбивается с поверхности, если с ним сталкивается достаточно энергичный фотон, а энергия каждого фотона пропорциональна частоте световой волны h ν = E электрона + const., где константа – работа выхода электрона, зависящая от природы металла. Чтобы вырваться с поверхности, электрон должен получить определенное количество энергии, однако, если частота света слишком мала, энергии сообщаемой фотоном недостаточно, чтобы вырвать электрон. Энергия каждого фотона зависит от частоты света, а с ростом интенсивности увеличивается количество падающих фотонов, следовательно, чтобы увеличить скорость электрона нужно увеличить частоту света, а чтобы увеличить количество электронов – интенсивность.
- волновой вектор, длина которого связана с длиной волны λ, частотой ω и скоростью света с. Эйнштейн предположил, что электромагнитное поле передает только определенную порцию (квант) энергии, которая переносится частицей света – фотоном. Электрон выбивается с поверхности, если с ним сталкивается достаточно энергичный фотон, а энергия каждого фотона пропорциональна частоте световой волны h ν = E электрона + const., где константа – работа выхода электрона, зависящая от природы металла. Чтобы вырваться с поверхности, электрон должен получить определенное количество энергии, однако, если частота света слишком мала, энергии сообщаемой фотоном недостаточно, чтобы вырвать электрон. Энергия каждого фотона зависит от частоты света, а с ростом интенсивности увеличивается количество падающих фотонов, следовательно, чтобы увеличить скорость электрона нужно увеличить частоту света, а чтобы увеличить количество электронов – интенсивность.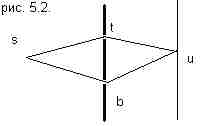
 .
.
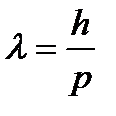
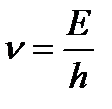 и длина волны
и длина волны 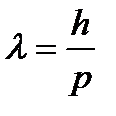 .
.

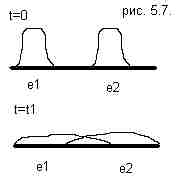 новая функция системы частиц при перестановке координат двух частиц не должна меняться.
новая функция системы частиц при перестановке координат двух частиц не должна меняться.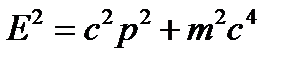 .
.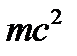 . Если система состоит из медленно движущихся частиц, то их энергия недостаточна для образования новых частиц. Сказанное относится к массивным частицам, но у фотона масса покоя равна нулю и для его образования не требуется больших релятивистских энергий. В квантовой теории поля фотон играет особую роль – он является частицей-переносчиком взаимодействия.
. Если система состоит из медленно движущихся частиц, то их энергия недостаточна для образования новых частиц. Сказанное относится к массивным частицам, но у фотона масса покоя равна нулю и для его образования не требуется больших релятивистских энергий. В квантовой теории поля фотон играет особую роль – он является частицей-переносчиком взаимодействия. определяет вероятность данного состояния. Если число частиц N точно известно, то
определяет вероятность данного состояния. Если число частиц N точно известно, то  , т.е. вектор состояния для любого фиксированного N нормирован на единицу.
, т.е. вектор состояния для любого фиксированного N нормирован на единицу. .
. .
. ,где
,где  – вектор состояния, характеризующий вакуум. Таким образом, получается одночастичное состояние, которое получается в результате рождения из вакуума одной частицы. Определение вакуума
– вектор состояния, характеризующий вакуум. Таким образом, получается одночастичное состояние, которое получается в результате рождения из вакуума одной частицы. Определение вакуума  , т.к. невозможно уничтожить частицу в состоянии в котором частиц нет. Вакуумный вектор состояние
, т.к. невозможно уничтожить частицу в состоянии в котором частиц нет. Вакуумный вектор состояние  имеет в квантовой теории поля особое значение, так как из него при помощи оператора а+, можно получить любые состояния, применив его соответствующее количество раз.
имеет в квантовой теории поля особое значение, так как из него при помощи оператора а+, можно получить любые состояния, применив его соответствующее количество раз. .
.

 где n, m – целые числа, обозначающие номера частиц.
где n, m – целые числа, обозначающие номера частиц. . Данные соотношения имеют место для полей, кванты которых имеют полуцелый спин и подчиняются принципу запрета Паули, запрещающего наличие в одной системе двух систем в одинаковых состояниях.
. Данные соотношения имеют место для полей, кванты которых имеют полуцелый спин и подчиняются принципу запрета Паули, запрещающего наличие в одной системе двух систем в одинаковых состояниях. Для описания этих процессов используются диаграммы Фейнмана, которые представляют собой графики движения частиц в 4-х мерном пространстве-времени. В диаграммах Фейнмана физическому процессу сопоставляется его графическая схема. Движение фотона отображается волнистой линией движение электрона – прямой, движение античастиц изображается как движение вспять по времени. Взаимодействие частиц на диаграмме изображается вершиной (или узлом), в котором сходятся две фермионных и одна бозонная линии (см. рис. 5.9). Линии, один из концов которых свободен, соответствуют свободным частицам. Данный рисунок иллюстрирует процесс испускания фотона электроном.
Для описания этих процессов используются диаграммы Фейнмана, которые представляют собой графики движения частиц в 4-х мерном пространстве-времени. В диаграммах Фейнмана физическому процессу сопоставляется его графическая схема. Движение фотона отображается волнистой линией движение электрона – прямой, движение античастиц изображается как движение вспять по времени. Взаимодействие частиц на диаграмме изображается вершиной (или узлом), в котором сходятся две фермионных и одна бозонная линии (см. рис. 5.9). Линии, один из концов которых свободен, соответствуют свободным частицам. Данный рисунок иллюстрирует процесс испускания фотона электроном. Квантовая хромодинамика
Квантовая хромодинамика e. При этом на единицу увеличивается заряд ядра атома Z → Z +1, а атомный вес остается прежним. В 1934 г. Ферми создал теорию β-распада и для объяснения явления ввел гипотезу о существовании особого типа короткодействующих сил: слабого взаимодействия, действующего на расстояниях меньше чем 10–15.
e. При этом на единицу увеличивается заряд ядра атома Z → Z +1, а атомный вес остается прежним. В 1934 г. Ферми создал теорию β-распада и для объяснения явления ввел гипотезу о существовании особого типа короткодействующих сил: слабого взаимодействия, действующего на расстояниях меньше чем 10–15.


