
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила осциллятора атомного перехода
Принцип соответствия между классической и квантовой физикой, конкретизированный для случая излучательных переходов в атоме, называется спектроскопическим принципом соответствия. Его можно сформулировать следующим образом: атом при взаимодействии с электромагнитным полем ведет себя как набор классических осцилляторов, обладающих собственными частотами, равными частотам переходов между атомными уровнями энергии. Это значит, что каждому переходу между атомными состояниями
где Формулировка принципа соответствия с силой осциллятора в форме (3.39) отвечает дипольному приближению, критерий которого дается неравенством (3.24). В противном случае определение (3.39) должно быть обобщено, чтобы включить в себя недипольную часть взаимодействия электромагнитного излучения с атомными электронами. Кроме того, недипольность взаимодействия оказывается существенной, если матричный элемент дипольного момента в формуле (3.39) равен нулю. Такие переходы называются дипольно-запрещенными в противоположность дипольно-разрешенным переходам, когда
В терминах приведенной классификации состояний правила отбора для дипольного излучения водородоподобного иона сводятся к следующему. Разрешенными являются переходы, для которых орбитальное квантовое число изменяется на единицу: Помимо электронных переходов в дискретном спектре (связанно-связанные переходы), имеют место также переходы из связанных состояний в состояния непрерывного спектра (связанно-свободные переходы), для которых тоже вводится понятие силы осциллятора по формуле, аналогичной (3.39). Физически связанно-свободному переходу соответствует ионизация атома. В отличие от случая связанно-связанного перехода, сила осциллятора для связанно-свободного перехода в состояние с энергией
Силы осцилляторов связанно-связанных и связанно-свободных переходов в атоме удовлетворяют так называемому золотому правилу сумм, которое для переходов из основного состояния выражается равенством
где Cилы осцилляторов для ряда электронных переходов в атоме водорода приведены в таблице
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 939; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.184.214 (0.005 с.) |
 и
и  ставится в соответствие осциллятор с собственной частотой
ставится в соответствие осциллятор с собственной частотой  . Назовем эти осцилляторы осцилляторами переходов. Вклад осцилляторов переходов в отклик атома на электромагнитное воздействие пропорционален безразмерной величине, называемой силой осциллятора. Чем больше сила осциллятора, тем сильнее соответствующий переход. Сила осциллятора для перехода между состояниями дискретного спектра
. Назовем эти осцилляторы осцилляторами переходов. Вклад осцилляторов переходов в отклик атома на электромагнитное воздействие пропорционален безразмерной величине, называемой силой осциллятора. Чем больше сила осциллятора, тем сильнее соответствующий переход. Сила осциллятора для перехода между состояниями дискретного спектра  ––
––  –– определяется формулой
–– определяется формулой , (3.39)
, (3.39) –– статистический вес j -го состояния. Из формулы (3.39) следует равенство
–– статистический вес j -го состояния. Из формулы (3.39) следует равенство  , поскольку сила осциллятора для перехода с уменьшением энергии отрицательна. Согласно своему физическому смыслу сила осциллятора одноэлектронного атома всегда меньше единицы.
, поскольку сила осциллятора для перехода с уменьшением энергии отрицательна. Согласно своему физическому смыслу сила осциллятора одноэлектронного атома всегда меньше единицы.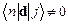 . Равенство или неравенство нулю дипольного момента перехода может быть предсказано на основании соображений симметрии состояний, между которыми происходит переход. Соотношения между характеристиками атомных состояний, позволяющие предсказать ненулевое значение величины
. Равенство или неравенство нулю дипольного момента перехода может быть предсказано на основании соображений симметрии состояний, между которыми происходит переход. Соотношения между характеристиками атомных состояний, позволяющие предсказать ненулевое значение величины  , называются правилами отбора для дипольного излучения. Наиболее простой вид эти правила имеют для водородоподобного иона. Систематика его электронных состояний в пренебрежении спин-орбитальным взаимодействием весьма проста. Энергетический уровень с главным числом
, называются правилами отбора для дипольного излучения. Наиболее простой вид эти правила имеют для водородоподобного иона. Систематика его электронных состояний в пренебрежении спин-орбитальным взаимодействием весьма проста. Энергетический уровень с главным числом  (см. формулу (3.16)) имеет
(см. формулу (3.16)) имеет  -кратное вырождение, которое возникает следующим образом. Во-первых, имеется специфическое для водородоподобного иона вырождение по квантовому числу орбитального момента
-кратное вырождение, которое возникает следующим образом. Во-первых, имеется специфическое для водородоподобного иона вырождение по квантовому числу орбитального момента  : энергию
: энергию  имеют состояния атомного электрона с
имеют состояния атомного электрона с  , обозначаемые как
, обозначаемые как  . Напомним, что численным обозначениям
. Напомним, что численным обозначениям 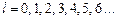 соответствуют буквенные:
соответствуют буквенные:  Далее, каждое состояние
Далее, каждое состояние  вырождено по значению проекции орбитального момента электрона на выделенную ось. Это вырождение носит общий характер и связано со сферической симметрией атомного потенциала. Квантовое число проекции момента количества движения
вырождено по значению проекции орбитального момента электрона на выделенную ось. Это вырождение носит общий характер и связано со сферической симметрией атомного потенциала. Квантовое число проекции момента количества движения 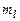 пробегает
пробегает  значение:
значение:  , чему соответствуют состояния
, чему соответствуют состояния 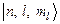 . Наконец, электронные состояния
. Наконец, электронные состояния  . Магнитное квантовое число при этом изменяется не более чем на единицу
. Магнитное квантовое число при этом изменяется не более чем на единицу  . В частности, если магнитное квантовое число не изменяется, то излучается (поглощается) линейно поляризованное изучение, в оставшихся случаях –– циркулярно поляризованное. Частным случаем правил отбора является тот факт, что средний дипольный момент атома в отсутствие внешних полей равен нулю:
. В частности, если магнитное квантовое число не изменяется, то излучается (поглощается) линейно поляризованное изучение, в оставшихся случаях –– циркулярно поляризованное. Частным случаем правил отбора является тот факт, что средний дипольный момент атома в отсутствие внешних полей равен нулю: 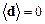 . Это обстоятельство может рассматриваться так же, как следствие сферической симметрии атома.
. Это обстоятельство может рассматриваться так же, как следствие сферической симметрии атома. ––
––  уже не является безразмерной величиной. Размерность
уже не является безразмерной величиной. Размерность  .
. , (3.40)
, (3.40) –– потенциал ионизации атома,
–– потенциал ионизации атома,  –– число электронов в атоме.
–– число электронов в атоме.


