Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6 Состояние э-м поля, вторичное квантованиеСтр 1 из 13Следующая ⇒
Силы осцилляторов для атома водорода Из этой таблицы вытекают следующие закономерности. Во-первых, для переходов с увеличением энергии сила осциллятора больше в случае увеличения орбитального квантового числа, т.е. переход
Парадокс Эйнштейна — Подольского — Розена Парадокс Эйнште́йна — Подо́льского — Ро́зена (ЭПР-парадокс) — попытка указания на неполноту квантовой механики с помощью мысленного эксперимента, заключающегося в измерении параметров микрообъекта косвенным образом, не оказывая на этот объект непосредственного воздействия. Целью такого косвенного измерения является попытка извлечь больше информации о состоянии микрообъекта, чем даёт квантовомеханическое описание его состояния. Изначально споры вокруг парадокса носили скорее философский характер, связанный с тем, что следует считать элементами физической реальности — считать ли физической реальностью лишь результаты опытов и может ли Вселенная быть разложена на отдельно существующие «элементы реальности» так, что каждый из этих элементов имеет своё математическое описание. Суть парадокса Согласно соотношению неопределённостей Гейзенберга, нет возможности одновременно точно измерить координату частицы и её импульс. Предполагая, что причиной неопределённости является то, что измерение одной величины вносит принципиально неустранимые возмущения в состояние и производит искажение значения другой величины, можно предложить гипотетический способ, которым соотношение неопределённостей можно обойти.
Допустим, две одинаковые частицы Если же законы квантовой механики в данном случае не нарушаются, то измерение импульса одной частицы равносильно измерению импульса второй частицы. Однако это создаёт впечатление мгновенного воздействия первой частицы на вторую в противоречии с принципом причинности.
Заголовок статьи в «The New York Times» от 4 мая 1935: «ЭЙНШТЕЙН АТАКУЕТ КВАНТОВУЮ ТЕОРИЮ: Учёный и двое его коллег находят её „неполной“, хотя и „корректной“». В 1927 году на Пятом Сольвеевском конгрессе Эйнштейн решительно выступил против «копенгагенской интерпретации» Макса Борна и Нильса Бора, трактующей математическую модель квантовой механики как существенно вероятностную. Он заявил, что сторонники этой интерпретации «из нужды делают добродетель», а вероятностный характер свидетельствует лишь о том, что наше знание физической сущности микропроцессов неполно. Так зародился спор Бора — Эйнштейна о физическом смысле волновой функции. В 1935 году Эйнштейн вместе с Борисом Подольским и Натаном Розеном написал статью «Можно ли считать квантово-механическое описание физической реальности полным?», в которой описал мысленный эксперимент, который впоследствии был назван парадоксом Эйнштейна — Подольского — Розена.
После публикации этой статьи Нильс Бор опубликовал статью с тем же названием, в которой он высказал несколько аргументов за вероятностное описание квантовой механики и определённую аналогию между положениями квантовой механики и эйнштейновской Общей теорией относительности. Бом в 1952 году рассмотрел возможность провести эксперимент (технически тогда еще не осуществимый), т. н. оптический вариант ЭПР-опыта, который смог бы разрешить спор Эйнштейна-Бора. В 1964 году Белл ввёл математический формализм, использующий дополнительные параметры, которые могли бы объяснить вероятностную природу квантовых явлений. По замыслу, полученные им неравенства должны были показать, может ли введение дополнительных параметров сделать описание квантовой механики не вероятностным, а детерминированным — в случае нарушения неравенств Белла такое детерминистическое описание с использованием дополнительных параметров невозможно. Таким образом, становилось возможным в эксперименте получить определённую величину, описывающую корреляции между удаленными измерениями, и на её основе сказать, имеет ли смысл описывать квантовые явления вероятностно или детерминировано. Результаты экспериментов, проведённых в 1972 году Стюартом Дж. Фридманом и Джоном Ф. Клаузером в Калифорнийском университете в Беркли, согласовывались с квантовой механикой, и было зафиксировано нарушение неравенств Белла. Затем в Гарвардском университете Р.А. Хольт и Ф.М. Пипкин получили результат, расходящийся с квантовой механикой, но удовлетворяющий неравенствам Белла. В 1976 году в Хьюстоне Эдвард С. Фрай и Рэднделл. С. Томпсон изготовили гораздо более совершенный источник коррелированных фотонов, и их результат совпал с предсказаниями квантовой механики. Они установили нарушение неравенств Белла. Все эти эксперименты выполнялись с одноканальными поляризаторами, и отличались лишь источниками коррелированных фотонов и их получением. При такой упрощенной экспериментальной схеме используются поляризаторы, пропускающие свет, поляризованный параллельно a (или b), но не пропускающие свет в ортогональном направлении. Поэтому можно получить только часть величин, нужных для вычисления корреляции между удаленными измерениями. Для того, чтобы повысить точность экспериментов, было необходимо иметь стабильный и хорошо управляемый источник запутанных фотонов и использовать двухканальный поляризатор. В 1982—1985 гг. Алан Аспе, используя соответствующее оборудование, поставил серию более сложных экспериментов, результаты которых также совпали с предсказаниями квантовой механики и продемонстрировали нарушение неравенств Белла. Постановка экспериментов и проверка деталей идут до сих пор, и по мнению А. Аспе, в конечном счёте должны привести к окончательному эксперименту, не оставляющему никаких «дыр». Но пока такой эксперимент так и не был осуществлён, и приверженцы теории скрытых параметров указывают на всё новые детали и возможности для построения полной квантово-механической теории. Пока ясно только то, что самые простые виды теорий скрытых параметров (с локальными параметрами) не соответствуют действительности, а более сложные ещё не построены.
Объяснение парадокса Эксперимент ЭПР, с точки зрения его авторов, позволяет одновременно точно измерить координату и импульс частицы. В то же время — в квантовой механике утверждается, что таковое невозможно. На основании этого Эйнштейн, Подольский и Розен сделали вывод о неполноте квантовой теории. На самом деле эксперимент, описанный ЭПР, не противоречит квантовой механике и легко анализируется с её помощью. Кажущееся противоречие возникает потому, что термин «измерение» имеет несколько различный смысл в классической и квантовой теории. Измерение и состояние В квантовой механике в результате измерения происходит изменение состояния системы. Если у частицы измеряется импульс В состоянии В эксперименте ЭПР после измерения импульса у первой частицы, вторая частица также переходит в состояние с определённым импульсом. У неё можно измерить координату, однако сразу после такого измерения импульс частицы изменится, поэтому говорить, что произошло одновременное измерение координаты и импульса смысла не имеет. Нелокальность Необычность эксперимента ЭПР, с точки зрения классической физики, состоит в том, что в результате измерения импульса первой частицы, изменяется состояние у второй, когда частицы находятся сколь угодно далеко друг от друга. В этом проявляется нелокальный характер квантовой теории. Система, состоящая из двух частиц, состояние которых описывается единой волновой функцией, не является простой «суммой» этих частиц, даже если между ними нет взаимодействия. При проведении измерения состояние такой составной системы может измениться. С этой точки зрения является некорректной исходная посылка ЭПР касательно того, что «так как во время измерения эти две системы уже не взаимодействуют, то в результате каких бы то ни было операций над первой системой во второй системе уже не может получиться никаких реальных изменений». Волновая функция — это нелокальная величина, и большое расстояние между частицами при измерении, которое её изменяет, существенной роли не играет.
Мысленный эксперимент ЭПР и связанная с ним нелокальность квантовой механики, в настоящее время привлекает широкое внимание в связи с экспериментами по квантовой телепортации. В историческом плане парадокс Эйнштейна — Подольского — Розена и последовавшая затем дискуссия между Бором и Эйнштейном сыграли важную роль для прояснения таких ключевых физических понятий, как «измерение», «полнота теории», «физическая реальность» и «состояние системы». Принцип тождественности В соответствии с принципом тождественности все частицы для нас являются неразличимыми, одинаковыми. Таким образом, при попытке косвенного определения точных значений одновременно импульса и координаты электрона в случае рождения электрон-позитронной пары, измерив точно импульс позитрона, при измерении «точной» координаты электрона мы не сможем сказать, тот ли это электрон или «другой» электрон измерительного прибора, что внесёт в наш эксперимент неопределённость в соответствии с принципом неопределённости. Также вместо точного измерения параметра «нужной» нам частицы мы можем измерить параметр одной из тождественных виртуальных частиц, существование которых было подтверждено экспериментально благодаря эффекту Казимира, что также может внести в наш эксперимент ошибку-неопределённость. Эффект Казимира — эффект, заключающийся во взаимном притяжении проводящих незаряженных тел под действием квантовых флуктуаций в вакууме. Чаще всего речь идёт о двух параллельных незаряженных зеркальных поверхностях, размещённых на близком расстоянии, однако эффект Казимира существует и при более сложных геометриях. Причиной эффекта Казимира являются энергетические колебания физического вакуума из-за постоянного рождения и исчезновения в нём виртуальных частиц. Эффект был предсказан голландским физиком Хендриком Казимиром (Hendrik Casimir, 1909—2000) в 1948 году, а позднее подтверждён экспериментально.
«Критерий физической реальности» и понятие «полноты физической теории
Альберт Эйнштейн и Нильс Бор Для того, чтобы наиболее точно и формально высказать, в чем квантовая механика неполна, Эйнштейн, Подольский, Розен в своей статье формулируют «критерий физической реальности»:
А также указывают, что они понимают под «полнотой физической теории»:
После чего авторы отмечают известный факт из квантовой механики:
И отсюда делается закономерный вывод: «квантовомеханическое описание реальности посредством волновой функции не полно». Затем рассматривается случай зацепленных состояний и авторы приходят к выводу, что «две физические величины с некоммутирующими операторами могут быть реальными одновременно». А это означает, что их можно было бы измерить одновременно, что противоречит неопределенности Гейзенберга. Аналогично и в случае когда имеется квантовомеханическое описание реальности посредством матрицы плотности — не полно. Критика парадокса Ответ Бора Ответ Бора начинается с заявления:
и далее Бор достаточно подробно рассматривает ряд измерений в экспериментах. Он отрицает, что можно говорить о какой-либо неполноте квантовомеханического описания. А вероятностные измерения связаны с невозможностью контролировать обратное действие объекта на измерительный прибор (то есть учёт переноса количества движения в случае измерения положения и учет смещения в случае измерения количества движения). После чего рассматривает различные способы устранения такого влияния и приходит к выводу:
Здесь мы можем заметить, что Бор, по сути, отвечает как бы на вопрос «Правильна ли теория?». Да, она правильна и результаты опыта это подтверждают. Эйнштейн и соавторы же делают акцент на вопросе «Является ли даваемое теорией описание полным?», то есть может ли быть найдено более удовлетворительное математическое описание, которое соответствовало бы физической реальности, а не проводимым нами измерениями. Бор же стоит на позиции, что физическая реальность есть то, что дает физическое измерение в эксперименте. Эйнштейн же, по видимому, допускает, что физическая реальность может отличаться от того, что нам дано в опыте, лишь бы математическое описание позволяло бы сделать прогноз с достоверностью (то есть вероятностью, равной единице) значения некоторой физической величины. Поэтому Фок замечает, что Эйнштейн и Бор вкладывают разный смысл в некоторые термины, и вся аргументация с той и другой стороны подчинена изначальной позиции, которую выбрал для себя оппонент:
Таким образом, данный спор содержит в своей основе вопрос о достаточности и необходимости тех или иных постулатов физической теории и исходящем из этого философском понимании физической реальности (природы) и о том, какое описаниефизических явлений может удовлетворить исследователя. И в решении данного вопроса отчетливо видна важная связь философии и физики[16]. Оптический вариант мысленного ЭПР-опыта, предложенный Бомом Бом в 1952 году в последней главе своей книги[17] отмечает, что в критерии физической реальности, данном в ЭПР-парадоксе, неявно присутствуют два предположения: 1. Вселенная может быть правильно разложена на различные и отдельно существующие «элементы реальности»; 2. Каждый из этих элементов может быть представлен точно определенной математической величиной. Дальше Бом отмечает, что если искать доказательства концепции изложенной в ЭПР-парадоксе, то это должно привести к поискам более полной теории, выраженной, например, в виде теории скрытых параметров. Важным вкладом Бома в решение этого парадокса считают то, что он предложил реальный физический эксперимент, который позволил бы в частном виде реализовать мысленный ЭПР-эксперимент, на базе двух фильтров Штерна-Герлаха, оптическим аналогом которых является поляризатор, который использовался в реальных опытах. Хотя в то время предложенный эксперимент было невозможно организовать технически, тем не менее, была показана возможность постановки реального опыта для проверки философских позиций Эйнштейна и Бора.
Мысленный эксперимент Эйнштейна-Подольского-Розена-Бома с фотонами. Два фотона v1 и v2, испущенные в зацепленном состоянии, анализируются линейными поляризаторами с ориентациями a и b. Можно измерять вероятности одиночной или совместной регистрации на выходе каналов поляризаторов
Фильтр Штерна — Герлаха (поляризатор)
Суть опыта состоит в следующем: источник S испускает два фотона в зацепленных состояниях, которые можно описать уравнением Далее можно использовать тот факт, что зацепленное состояние не может быть преобразовано в произведение двух состояний, ассоциированных с состоянием каждого из фотонов, то есть с независимыми состояниями фотонов (поэтому, например, в этом эксперименте нельзя приписать каждому из участвующих фотонов определенную поляризацию). Такое состояние описывает именно систему объектов целиком. Тогда благодаря зацепленности при измерении спина (момента вращения) второго фотона должно получаться противоположное значение для компоненты y. То есть будет получено косвенное измерение второй частицы, как это и было описано в мысленном ЭПР — эксперименте. И если бы это было справедливо для всех измерений (при различных процессах, и при произвольных углах ориентации поляризаторов), то это противоречило бы утверждению неопределенности Гейзенберга, что нельзя измерить достоверно две величины одной частицы. Еще одним важным предложением Бома стало то, что исследователь может переориентировать аппаратуру в произвольном направлении пока частицы еще разлетаются и таким образом получить определенное значение спина в любом выбранном им направлении. Поскольку эта переориентация выполняется без возмущения второй частицы, то, приняв критерий физической реальности Эйнштейна, можно определить, получается ли результат измерения лишь в момент самого измерения (что соответствует положению квантовой механики) или же он уже предопределен до измерения, и, если бы были известны скрытые параметры, то стало бы возможно это определить достоверно, с вероятностью 1. Объясняя же возможные последствия подтверждения квантового описания в таком эксперименте Бом пишет:
Таким образом, Бом явным образом указывает, что квантовая механика является неполной теорией в том смысле, что не может сопоставить каждому элементу реальности определенную математическую величину. В то время как Вселенная, по его мнению, может быть разложена на различные и отдельно существующие «элементы реальности». Популяризация Для популярного донесения парадокса Д. Мермин предлагает сконструировать простое устройство. Устройство должно состоять из излучателя частиц и двух детекторов. Две одинаковые частицы испускаются к каждому из них. Поймав частицу, детектор даёт двоичный ответ (0 или 1), зависящий от частицы и своего трёхпозиционного переключателя настройки. Детектирование пары частиц должно дать одинаковые ответы 1. всякий раз, когда детекторы настроены одинаково и 2. по статистике в половине случаев, когда они настроены случайным образом. Первое свойство требует, чтобы функции отображения детекторов, позиция переключателя ∈ {1,2,3} ↦ отклик ∈ {0,1}, совпадали. То есть для приёма каждой пары, из восьми возможных функций, 000, 001, 010, 011, 100, 101, 110 и 111 выбирается одна и реализуется на обоих детекторах. Выбор 000 или 111 приведёт к 100% совпадению показаний детекторов. Если же детекторы реализуют одну из шести оставшихся функций, одна из цифр вытягивается случайно настроенным переключателем в 2/3 случаев, другая — с вероятностью 1/3. Вероятность совпадения двух ответов при этом составит (⅔)² + (⅓)² = 5/9. Так что, каков бы ни был алгоритм автомата, корреляция неизбежно превысит 50%, нарушая второе требование. Но поскольку такую машину всё-таки соорудить можно (например, располагая позиции поляризаторов под 120° как в опыте Бома), то никакого детерминизма (параметров) не может быть даже в скрытой форме. Вместо этого корреляции откликов поддерживаются за счёт передачи информации от одной «измеренной» частицы к другой быстрее, чем произойдёт второе измерение. · Неравенства Белла Носки Бертлмана Кот Шрёдингера Волновая функция Редукция фон Неймана · Объективная редукция Квантовые измерения Квантовая телепортация · Литература · Бом Д. Квантовая теория = Quantum Theory // New York: Prentice Hall. 1989 reprint, New York: Dover, ISBN 0-486-65969-0. — 1951., стр. 700, гл. 12, п. 15 · Блохинцев Д. И. Основы квантовой механики. — М.-Л.: ГИТТЛ, 1949. · Блохинцев Д. И. Основы квантовой механики (3-е изд.) М.: Высшая школа, 1961. · Reid M. D. et al. Colloquium: the Einstein-Podolsky-Rosen paradox: From concepts to applications (англ.) // Reviews of Modern Physics. — 2009. — Т. 81. — № 4. — С. 1727–1751. DOI:10.1103/RevModPhys.81.1727
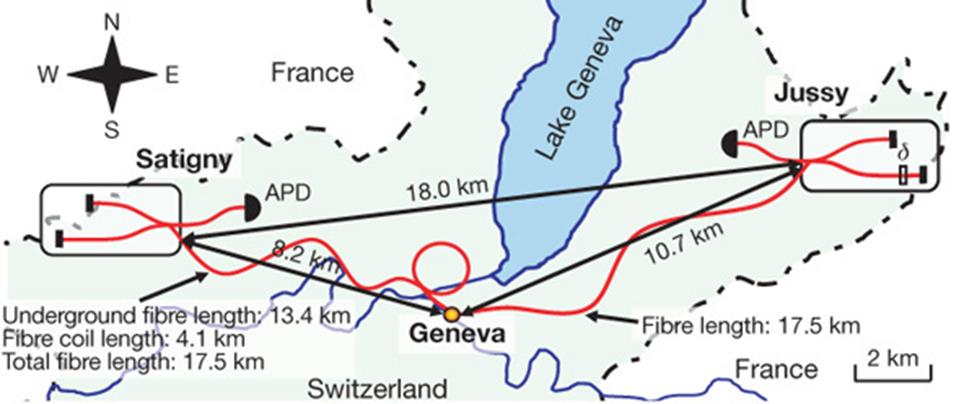
Лекция 12 Ква́нтовая запу́танность — квантовомеханическое явление, при котором квантовые состояния двух или большего числа объектов оказываются взаимозависимыми. Такая взаимозависимость сохраняется, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий, что находится в логическом противоречии с принципом локальности. Например, можно получить пару фотонов, находящихся в запутанном состоянии, и тогда если при измерении спина первой частицы спиральность оказывается положительной, то спиральность второй всегда оказывается отрицательной, и наоборот. Современный этап Современные версии описанного выше эксперимента создают сегменты Sa и Sb такой длины, чтобы регистрация фотонов происходила в заведомо не связанных известными взаимодействиями областях пространства-времени. В 2007 году исследователям из Мичиганского университета удалось разнести запутанные фотоны на рекордное в тот момент расстояние в 1 метр. В 2008 году группе швейцарских исследователей из Университета Женевы удалось разнести два потока запутанных фотонов на расстояние 18 километров. Помимо прочего, это позволило произвести временны́е измерения с недостижимой ранее точностью. В результате было установлено, что если некое скрытое взаимодействие и происходит, то скорость его распространения должна как минимум в 100 000 раз превышать скорость света в вакууме. При меньшей скорости временные задержки были бы замечены. Суть эксперимента
Геометрия эксперимента. Пары запутанных фотонов порождались в Женеве, затем фотоны посылались вдоль оптоволоконных кабелей одинаковой длины (отмечены красным цветом) в два приемника (отмечены буквами APD), отстоящими друг от друга на 18 км. Изображение из обсуждаемой статьи в Nature
Новизна данной работы лишь в том, что эксперимент длился долго. Квантовые корреляции наблюдались непрерывно и не исчезали ни в какое время суток. Почему это важно? Если гипотетическое взаимодействие переносится некоторой средой, то у этой среды будет выделенная система отсчета. Из-за вращения Земли лабораторная система отсчета движется относительно этой системы отсчета с разной скоростью. Это значит, что промежуток времени между двумя событиями детектирования двух фотонов будет для этой среды всё время разным, в зависимости от времени суток. В частности, будет и такой момент, когда эти два события для этой среды будут казаться одновременными. (Тут, кстати, используется тот факт из теории относительности, что два одновременных события будут одновременными во всех инерциальных системах отсчета, движущихся перпендикулярно соединяющей их линии). Если квантовые корреляции осуществляются за счет описанного выше гипотетического взаимодействия и если скорость этого взаимодействия конечна (пусть и сколь угодно большая), то в этот момент корреляции бы исчезли. Поэтому непрерывное наблюдение корреляций в течение суток полностью закрыло бы эту возможность. А повторение такого эксперимента в разные времена года закрыло бы эту гипотезу даже с бесконечно быстрым взаимодействием в своей, выделенной системе отсчета. К сожалению, этого достичь не удалось из-за неидеальности эксперимента. В этом эксперименте для того, чтобы сказать, что корреляции действительно наблюдаются, требуется накапливать сигнал в течение нескольких минут. Исчезновение корреляций, например, на 1 секунду этот эксперимент не смог бы заметить. Именно поэтому авторы не смогли полностью закрыть гипотетическое взаимодействие, а лишь получили ограничение на скорость его распространения в своей выделенной системе отсчета, что, конечно, сильно снижает ценность полученного результата.
Летом того же года другой группе исследователей из австрийского Института квантовой оптики и квантовой информации, включая Цайлингера, удалось поставить ещё более масштабный эксперимент, разнеся потоки запутанных фотонов на 144 километра, между лабораториями на островах Ла Пальма и Тенерифе. Обработка и анализ столь масштабного эксперимента продолжаются, последняя версия отчёта была опубликована в 2010 году. В данном эксперименте удалось исключить возможное влияние недостаточного расстояния между объектами в момент измерения и недостаточной свободы выбора настроек измерения. В результате были ещё раз подтверждены квантовая запутанность и, соответственно, нелокальная природа реальности. Правда, осталось третье возможное влияние — недостаточно полной выборки. Эксперимент, в котором все три потенциальных влияния будут исключены одновременно, на сентябрь 2011 года является вопросом будущего. В большинстве экспериментов с запутанными частицами используются фотоны. Это объясняется относительной простотой получения запутанных фотонов и их передачи в детекторы, а также бинарной природой измеряемого состояния (положительная или отрицательная спиральность). Спиральность — характеристика состояния элементарной частицы. Представляет собой проекцию спина частицы на направление движения. Используется при описании элементарных частиц, движущихся со скоростью света или близкой к ней. Различают: 1. Отрицательную или «левую» — спин направлен против направления движения частицы; 2. Положительную или «правую» — спин направлен по движению частицы. Спиральность частицы h определяется нормированным скалярным произведением векторов спина частицы на её импульс:
Однако явление квантовой запутанности существует и для других частиц и их состояний. В 2010 году международный коллектив учёных из Франции, Германии и Испании получил и исследовал запутанные квантовые состояния электронов, то есть частиц с массой, в твёрдом сверхпроводнике из углеродных нанотрубок. В 2011 году исследователям из Института квантовой оптики общества Макса Планка удалось создать состояние квантовой запутанности между отдельным атомом рубидия и конденсатом Бозе-Эйнштейна, разнесёнными на расстояние 30 метров. При устойчивом английском термине Quantum entanglem
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.50 (0.063 с.) |
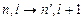 сильнее перехода
сильнее перехода  , если
, если  . Во-вторых, сумма сил осцилляторов для переходов в непрерывный спектр уменьшается с ростом орбитального квантового числа начального состояния, т.е. состояния с большим орбитальным моментом труднее ионизировать. В-третьих, наибольшей силой осциллятора обладают переходы в состояние с ближайшим главным квантовым числом. В-четвертых, силы осцилляторов для переходов с нижних уровней в состояния с большими квантовыми числами
. Во-вторых, сумма сил осцилляторов для переходов в непрерывный спектр уменьшается с ростом орбитального квантового числа начального состояния, т.е. состояния с большим орбитальным моментом труднее ионизировать. В-третьих, наибольшей силой осциллятора обладают переходы в состояние с ближайшим главным квантовым числом. В-четвертых, силы осцилляторов для переходов с нижних уровней в состояния с большими квантовыми числами  убывают как
убывают как 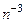 . Эти закономерности определяют вероятности соответствующих излучательных переходов в атоме водорода. Важным свойством силы осциллятора для водородоподобного иона является независимость данной величины от заряда ядра иона
. Эти закономерности определяют вероятности соответствующих излучательных переходов в атоме водорода. Важным свойством силы осциллятора для водородоподобного иона является независимость данной величины от заряда ядра иона 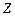 . Это легко увидеть из определения (3.39). В нем фигурируют две величины, зависящие от заряда ядра: частота перехода
. Это легко увидеть из определения (3.39). В нем фигурируют две величины, зависящие от заряда ядра: частота перехода  и матричный элемент дипольного момента перехода
и матричный элемент дипольного момента перехода  . Если учесть, что
. Если учесть, что 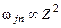 (см. формулу (3.17)), а
(см. формулу (3.17)), а  (по аналогии с (3.7)), то сразу получаем требуемое утверждение.
(по аналогии с (3.7)), то сразу получаем требуемое утверждение. и
и  образовались в результате распада третьей частицы
образовались в результате распада третьей частицы  . В этом случае, по закону сохранения импульса, их суммарный импульс
. В этом случае, по закону сохранения импульса, их суммарный импульс 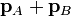 должен быть равен исходному импульсу третьей частицы
должен быть равен исходному импульсу третьей частицы  , то есть, импульсы двух частиц должны быть связаны. Это даёт возможность измерить импульс одной частицы (
, то есть, импульсы двух частиц должны быть связаны. Это даёт возможность измерить импульс одной частицы ( рассчитать импульс второй (
рассчитать импульс второй (
 , то она переходит в состояние, описываемое волновой функцией
, то она переходит в состояние, описываемое волновой функцией  . Повторные измерения импульса в этом состоянии всегда будут приводить к одному и тому же
. Повторные измерения импульса в этом состоянии всегда будут приводить к одному и тому же 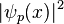 в некоторой точке пространства
в некоторой точке пространства  . Однако состояние частицы после такого измерения изменится: она перейдёт в состояние с определённым значением координаты
. Однако состояние частицы после такого измерения изменится: она перейдёт в состояние с определённым значением координаты 




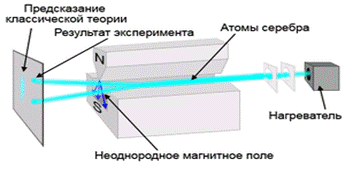

 Линейная поляризация
Линейная поляризация

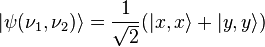 . Эти фотоны распространяются в противоположных направлениях вдоль оси Oz, а зацеплены по осям Ox и Oy. Исследователь может измерить одну из компонент (x, y или z) спина первого фотона, но не больше чем одну за опыт. Например, для частицы 1 мы сделаем измерение по оси Ox и получим таким образом компоненту x.
. Эти фотоны распространяются в противоположных направлениях вдоль оси Oz, а зацеплены по осям Ox и Oy. Исследователь может измерить одну из компонент (x, y или z) спина первого фотона, но не больше чем одну за опыт. Например, для частицы 1 мы сделаем измерение по оси Ox и получим таким образом компоненту x.