
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая термодинамика ⇐ ПредыдущаяСтр 2 из 2
Вывод уравнений феноменологической термодинамики на основе полученных статистических соотношений для системы из N частиц, находящихся в i-тых состояниях с вероятностью pi:
где
Тогда Рассмотрим в общем виде изменение математического ожидания (среднего значения) энергии <
Здесь
Для осуществления 1-го способа изменения энергии (по типу dQ) можно объединить две системы с различными значениями Для осуществления 2-го способа изменения энергии (по типу dA) можно изменить внешние условия системы (например, её объём V с помощью некоторого поршня, давящего на систему, т.е. изменяющего координаты Общее выражение
Связав во 2-ом способе изменение энергии системы (по типу dA) с изменением её внешних координат
где
Тогда Так как или
Статическая “средняя” сила в макросистеме идеального газа. Статическое вычисление силы давления и вывод уравнения состояния
Итак, рассматривая 2-ой способ изменения энергии системы через совершение работы dA: где
Поскольку как было показано ранее
то для средней силы можно записать Так как С учетом равенства Теперь, рассматривая давление Р в системе идеального газа как среднюю статическую силу, связанную с изменением его объёма V, получим:
где согласно прежним вычислениям Последнее выражение получено исходя из аддитивности энтропии:
и
Если рассматривать систему из неразличимых частиц, то полная неопределенность
Тогда для 1-го моля частиц
Используя формулу Стирлинга для
Отсюда нужная нам производная Так как для 1-го моля вещества
Полученное статическое распределение частиц по энергиям позволяет рассчитать среднее изменение количества движения частиц при их упругом взаимодействии со стенкой, образующей газовый объём V, т.е. рассчитать то, что называется давлением газа. Для этого вернемся к взаимосвязи энергии и импульса (ограничиваясь движением в одном направлении i, перпендикулярном стенке)
причем вероятность обладания этой скоростью
Где учтено, что частица может двигаться либо вправо, либо влево при одной и той же абсолютной скорости Так как за промежуток времени
Так как давление есть сила, равная изменению количества движения на единицу площади стенки в единицу времени, то поделив предыдущее выражение на
Для одного моля вещества
Для одной частицы (на ящик приходится одна частица):
Математическое ожидание энергии:
“Острота” распределения вероятностей задается дисперсией:
Относительное отклонение (для одной частицы) будет равно:
т.е. хотя вероятность выпадения герба при бросании монеты равна Для N частиц средняя энергия равна энергии одной частицы умноженной на N:
(здесь использована аппроксимация Стирлинга Дисперсия для N частиц: Относительное отклонение для N~6*1023 (одного моля вещества): Рассмотрим в общем виде изменении энтропии:
Так как по первому закону термодинамики:
где
где Тогда для общего изменения энтропии получим:
Константу K, которая в своё время была введена как произвольная постоянная в неопределенности S положим равной постоянной Больцмана K=k, тогда получаем второй закон термодинамики:
- физическая энтропия, связанной с (теплообменом) передачей теплоты dQ и производством работы dA при температуре системы T.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.76.43 (0.05 с.) |








 Вероятность pi находится на основе минимизации
Вероятность pi находится на основе минимизации  информационной энтропии Шеннона методом Джейнса с
информационной энтропии Шеннона методом Джейнса с  использованием неопределенных множителей Лагранжа
использованием неопределенных множителей Лагранжа  для дополнительных условий
для дополнительных условий
 из (1)
из (1) из (2),
из (2), 

 >
>


 (другое общепринятое обозначение работы dW)
(другое общепринятое обозначение работы dW) - представляет собой такой способ изменения энергии, при котором изменяются вероятности распределения её уровней при сохранении их значений
- представляет собой такой способ изменения энергии, при котором изменяются вероятности распределения её уровней при сохранении их значений - наоборот, сохраняет распределение вероятностей при изменении уровней энергии
- наоборот, сохраняет распределение вероятностей при изменении уровней энергии 
 , это из соотношения
, это из соотношения  т.е. для данного набора значений
т.е. для данного набора значений  средняя энергия зависит только от
средняя энергия зависит только от  то увеличение
то увеличение  , а так как
, а так как  её частиц – их потенциальную энергию). Этот способ изменения энергии называется работой.
её частиц – их потенциальную энергию). Этот способ изменения энергии называется работой. - соответствует первому началу термодинамики по типу dA
- соответствует первому началу термодинамики по типу dA , связанными с этими изменениями по соотношению:
, связанными с этими изменениями по соотношению:
 - среднее значение силы
- среднее значение силы - её (вероятностные силы) составляющие, связанные с изменением
- её (вероятностные силы) составляющие, связанные с изменением  состояния
состояния  сохранении распределения вероятностей
сохранении распределения вероятностей 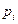 как и в равновесном
как и в равновесном  состоянии, т.е. при обратимом протекании процессов совершения работы (без трения)
состоянии, т.е. при обратимом протекании процессов совершения работы (без трения)
 , то
, то  можно записать в виде
можно записать в виде 
 , которое согласно уравнению
, которое согласно уравнению  приводится к легко запоминающейся форме:
приводится к легко запоминающейся форме:
 - по первому способу
- по первому способу (при сохранении распределения вероятностей
(при сохранении распределения вероятностей  ) с изменением её внешних координат
) с изменением её внешних координат  , т.е.
, т.е. 
 - среднее значение (мат.ожидание) действующей силы
- среднее значение (мат.ожидание) действующей силы - вероятностные составляющие этой силы, связанные с изменением уровней энергии системы
- вероятностные составляющие этой силы, связанные с изменением уровней энергии системы  при изменении её внешней координаты
при изменении её внешней координаты 
 ,
,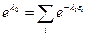 , то
, то 
 ,
,  , получим легко запоминающуюся форму для “средней” действующей силы
, получим легко запоминающуюся форму для “средней” действующей силы  ;
;  ,
, 
 ,
, - для одной частицы или
- для одной частицы или  - для 1-го моля частиц с числом частиц -
- для 1-го моля частиц с числом частиц - 
 - для 1-ой частицы, где
- для 1-ой частицы, где 
 - для 1-го моля частиц с числом частиц -
- для 1-го моля частиц с числом частиц - 
 включает в себя такую величину
включает в себя такую величину  возникающую в следствии того, что
возникающую в следствии того, что  способами, т.е. состояния, которые отличаются друг от друга только заменой тождественных частиц на самом деле неотличимы друг от друга и должны считаться одним состоянием. Следовательно, для системы
способами, т.е. состояния, которые отличаются друг от друга только заменой тождественных частиц на самом деле неотличимы друг от друга и должны считаться одним состоянием. Следовательно, для системы  будет меньше чем в случае неотличимых частиц, т.е. должна быть уменьшена на
будет меньше чем в случае неотличимых частиц, т.е. должна быть уменьшена на  , т.к. эта поправка не сказывается на энергии
, т.к. эта поправка не сказывается на энергии  . В результате получим:
. В результате получим: , где
, где 
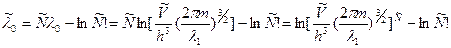
 , получим
, получим
 , и следовательно
, и следовательно  с учетом
с учетом  (универсальная газовая постоянная), то в итоге получаем уравнение состояния идеального газа в статическом виде:
(универсальная газовая постоянная), то в итоге получаем уравнение состояния идеального газа в статическом виде:
 ,
, составляет
составляет ,
, .
. частицы находящиеся на расстоянии
частицы находящиеся на расстоянии  от стенки и имеющие скорость
от стенки и имеющие скорость  по направлению, перпендикулярном к ней, при ударе о неё передающей свой импульс
по направлению, перпендикулярном к ней, при ударе о неё передающей свой импульс  и отскакивают от неё с той же энергией (той же абсолютной скоростью), то полное изменение количества движения в расчете на одну частицу будет равно
и отскакивают от неё с той же энергией (той же абсолютной скоростью), то полное изменение количества движения в расчете на одну частицу будет равно  , а в расчете на все частицы, находящие в объёме
, а в расчете на все частицы, находящие в объёме  , где A –площадь стенки, при их средней плотности
, где A –площадь стенки, при их средней плотности  в ограждённом стенкой газовом объёме V, составляет:
в ограждённом стенкой газовом объёме V, составляет: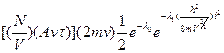
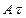 и просуммировав его по всем i, получим:
и просуммировав его по всем i, получим:
 произведение
произведение  и в итоге получим:
и в итоге получим: - уравнение состояния идеального газа
- уравнение состояния идеального газа


 ,
, , предсказание для одного броска довольно часто может быть ошибочным.
, предсказание для одного броска довольно часто может быть ошибочным.
 )
)

 ,
, 



 ;
;  зависит только от
зависит только от  (для первого способа изменения энергии), а также от внешних условий
(для первого способа изменения энергии), а также от внешних условий  (силового поля) для второго способа изменения энергии), то в общем случае можно записать:
(силового поля) для второго способа изменения энергии), то в общем случае можно записать: ,
, т.е.
т.е. 
 - обозначено некоторое значение силы
- обозначено некоторое значение силы - второе начало термодинамики, где
- второе начало термодинамики, где  ,
, 




