Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование математической модели. Построенная математическая модель может быть исследована с помощью одного из методов линейного программирования — симплекс-метода или каким-либо другим.
Для возможности применения к построенной математической модели симплекс-метода необходимо иметь вместо системы неравенств систему равенств. Для этого в каждое из неравенств введем фиктивное неизвестное (дополнительное неизвестное)
Вводимые дополнительные неизвестные ( Решение задачи сводится к определению базисных решений с помощью составления последовательности симплекс-таблиц (табл. 3.3), обеспечивающих направленное движение к искомому оптимуму. Для облегчения расчетов вся исходная информация и промежуточные расчеты представляются в виде, так называемых, симплекс-таблиц (табл. 3.3,3.4, и т.д.)
Алгоритм симплекс-метода включает несколько этапов:.1. Проверка базисного решения ( 2. Проверка задачи на наличие решения. Ваш над каким-либо положительным коэффициентом при небазисной переменной в целевой функции нет ни одного столбца с неположительным коэффициентом, то задача имеет решение. Для данного класса задач решение всегда имеется. 3. Выбор из небазисных переменных той, которая при введении ее в базис увеличивает значение целевой функции. Обычно выбирают небазисную переменную с наибольшим положительным коэффициентом в последней строке. В нашей задаче можно выбрать любую из 4. Определение базисной переменной, которая должна быть выведена из базиса. Для этого определяем минимальное частное от деления соответствующих свободных членов и положительных коэффициентов столбца отмеченного звездочкой. Имеем: 1/0,25; 1/0,20; 1/0,24. Минимальное частное соответствует базисной переменной х5, эту строку отмечаем звездочкой. Коэффициент 0,25, находящийся на пересечении строки и столбца, отмеченных звездочками, называется разрешающим элементом (см. жирное число в табл. 3.3).
5. Ввод в базис небазисной переменной и выражение ее через новые небазисные переменные. В нашем примере вводим х) и выражаем ее через новый набор небазисных переменных -
6. Выражение остальных базисных переменных и целевой функции через новые небазисные переменные. В нашем примере базисные переменные х6 х7 выражаем через новый набор небазисных переменных –x5,x2,x3, x4. Для этого коэффициенты в строке с новой базисной переменной в новой таблице (в нашей задаче при х,) умножается на такое число, чтобы после сложения с преобразуемой строкой табл. 3.3 в столбце X/ появился 0. В соответствии со сказанным, для получения коэффициентов второй строки (см. табл. 3.4) умножаем коэффициенты строки х1 на множитель - 0,20. Множитель для каждой преобразуемой переменной и целевой функции (x6, х7, F) в новой табл. 3.4, равен обратной величине коэффициента, стоящего на пересечении преобразуемой переменной и вводимой в базис переменной. Складываем результаты умножения с соответствующими коэффициентами второй строки табл. 3.3. Результаты сложения заносим во вторую строку табл. 3.4, и т.д. После заполнения табл. 3.4 весь расчет начинается сначала с п. 1. И так до тех пор, пока не будет найдено оптимальное решение. Выясняем, решение не оптимально, так как в последней строке табл. 3.4 есть положительные коэффициенты при небазисных переменных. Решение есть. В качестве вводимой в базис переменной выберем х4, которой соответствует наибольший положительный коэффициент. Отмечаем столбец х4 звездочкой В качестве выводимой из базиса переменной берем х7 так как для нее частное от деления свободного члена на коэффициент при x7 минимально.
Отмечаем строку звездочкой. Разрешающий элемент равен 0,037 (см. жирное число в табл. 3.4). Затем составляется новая симплекс-таблица и так до тех пор, пока в последней строке коэффициенты при небазисных переменных будут неположительные. В системе из и уравнений с т неизвестными (и < т) общее число максимально допустимых базисных решений равно числу сочетаний из n по m.
В нашей задаче максимально допустимое число базисных решений будет равно:
Поиск оптимального решения заключается в направленном переходе от одного допустимого базисного решения к другому в направлении максимизации целевой функции. Общее число итераций в симплекс-методе ограничено сверху и, следовательно, оптимальное решение может быть достигнуто за конечное число шагов, обычно в несколько раз меньшее, чем максимально допустимое число итераций. Для снижения трудоемкости определения оптимального комплекта машин в условиях неполной определенности целесообразно использовать электронно-вычислительную технику, которая не только снижает трудоемкость требуемых вычислений, но и резко сокращает время поиска. Ниже приводится программа, написанная на языке программирования Фортран, для определения оптимального комплекта машин в условиях неполной определенности (прогр. 3.2). В результате расчета на печать выводятся: вероятности использования каждого комплекта машин P(J) и минимальные суммарные затраты при использовании оптимального комплекта машин. В условиях неполной определенности.
|
||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.220.114 (0.009 с.) |
 Тогда математическая модель может быть записана в таком виде:
Тогда математическая модель может быть записана в таком виде:
 образуют начальный базис (базисные переменные). Все другие переменные называются небазисными. В симплекс-методе вводится также понятие — базисное решение, в котором все небазисные переменные принимаются равными 0, а значения базисных переменных определяются из решения системы равенств. На начальном этапе базисное решение
образуют начальный базис (базисные переменные). Все другие переменные называются небазисными. В симплекс-методе вводится также понятие — базисное решение, в котором все небазисные переменные принимаются равными 0, а значения базисных переменных определяются из решения системы равенств. На начальном этапе базисное решение ) будет выглядеть так (0,0,0,0,1,1,1).
) будет выглядеть так (0,0,0,0,1,1,1).
 ) на оптимальность. Если все коэффициенты целевой функции F (последняя строка табл. 3.3) при небазисных переменных неположительные, то исходный базис оптимален, в нашей задаче для начального базисного решения (0, 0,0,0,1, 1, 1) все коэффициенты при небазисных переменных для базисного решения положительны, значит решение не оптимально. Значение же целевой функции для этого базисного решения равно 0.
) на оптимальность. Если все коэффициенты целевой функции F (последняя строка табл. 3.3) при небазисных переменных неположительные, то исходный базис оптимален, в нашей задаче для начального базисного решения (0, 0,0,0,1, 1, 1) все коэффициенты при небазисных переменных для базисного решения положительны, значит решение не оптимально. Значение же целевой функции для этого базисного решения равно 0.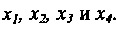 Выберем х1 отметим ее звездочкой.
Выберем х1 отметим ее звездочкой. Для этого все коэффициенты строки, отмеченной звездочкой, делим на разрешающий элемент, и результаты расчета записываем в новую симплекс-таблицу (табл. 3.4) в строку выведенной из базиса переменной.
Для этого все коэффициенты строки, отмеченной звездочкой, делим на разрешающий элемент, и результаты расчета записываем в новую симплекс-таблицу (табл. 3.4) в строку выведенной из базиса переменной.