
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение гармонической бегущей волныСтр 1 из 13Следующая ⇒
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими, т.е. описываются по закону синуса или косинуса. Часто гармоническую волну называют синусоидальной.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна тому расстоянию, на которое распространится гармоническая волна за время, равное периоду колебаний Т, т.е.
Учитывая, что частота v = 1 /T получаем l = v / v. (2) т.е. длина волны обратно пропорциональна частоте. Уравнение такой волны в общем случае имеет вид
Для характеристики волн используется волновое число
где w = 2 p/T = 2 pv – циклическая, (круговая) частота. С учетом (4) получим уравнение бегущей гармонической волны
где А – амплитуда волны, Основываясь на формуле Эйлера (
где физический смысл имеет лишь действительная часть выражения (6). Такая форма представления волны существенно облегчает математический действия. Фронт волны, волновые поверхности, фазовая скорость Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью (поверхностью постоянных фаз, фазовой поверхностью). Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени – один. Гармоническая бегущая волна (5) является плоской волной, т.к. ее волновые поверхности Уравнение гармонической сферической волны имеет вид
где r – радиальная координата. При распространении волны в непоглощающей среде A(r) ~ 1 /r.
Скорость v распространения гармонической волны называется фазовой скоростью. Она равна скорости перемещения волновой поверхности. Например, в случае плоской гармонической волны из условия
Волновое уравнение Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных.
где D – оператор Лапласа, v – фазовая скорость. Решением уравнения (9) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (5), которая не зависит от координат y и z волновое уравнение принимает вид
Соответствующей подстановкой можно убедится, что уравнению (11) удовлетворяет уравнение (5).
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.186.241 (0.006 с.) |
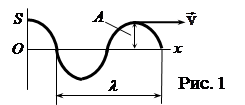 На рис.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x, т.е. приведена зависимость между смещением S частиц среды и расстоянием х этих частиц от источника колебаний О для фиксированного момента времени t.
На рис.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x, т.е. приведена зависимость между смещением S частиц среды и расстоянием х этих частиц от источника колебаний О для фиксированного момента времени t. . (1)
. (1) , (3)
, (3) , (4)
, (4) , (5)
, (5)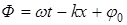 – фаза волны, j 0– начальная фаза.
– фаза волны, j 0– начальная фаза. ), уравнение (5) можно записать в экспоненциальной (комплексной) форме
), уравнение (5) можно записать в экспоненциальной (комплексной) форме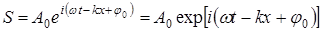 , (6)
, (6) представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.
представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х. , (7)
, (7)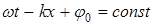 следует, что
следует, что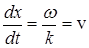 . (8)
. (8) , (9)
, (9) (10)
(10) . (11)
. (11)


