
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЗАДАЧА 4. Решить простейшую задачу классического вариационного исчисления. ⇐ ПредыдущаяСтр 2 из 2
Воспользуемся уравнением Эйлера-Лагранжа для решения простейшей задачи:
Подставим в исходное уравнение:
½
Исследуем экстремаль на предмет доставления функции максимума/минимума:
Проинтегрируем по частям:
ЗАДАЧА 5. Решить задачу Больца.
10.
Воспользуемся уравнением Эйлера-Лагранжа для решения задачи Больца:
Воспользуемся условиями трансверсальности:
Воспользуемся условиями трансверсальности:
Тогда условия трансверсальности запишутся:
Мы будем использовать эти уравнения как краевые условия для нахождения констант
Исследуем экстремаль на предмет доставления функции максимума/минимума:
Проинтегрируем по частям:
А также воспользуемся условием:
ЗАДАЧА 6. Решить изопериметрическую задачу.
Воспользуемся уравнением Эйлера-Лагранжа для решения изопериметрической задачи:
1) 2)
Воспользуемся краевыми условиями для нахождения констант:
Исследуем экстремаль на предмет доставления функции максимума/минимума:
Проинтегрируем по частям:
Так как
ЗАДАЧА 7. Решить задачу с подвижными концами.
Выпишем, как положено, функцию Лагранжа:
Воспользуемся уравнением Эйлера-Лагранжа для решения задачи с подвижными концами:
Воспользуемся условиями трансверсальности:
Тогда условия трансверсальности запишутся:
Запишем условие стационарности:
Пусть Пусть
Если
Рассмотрим
Рассмотрим Итак, мы получили:
Исследуем экстремаль
Также, стоит выразить значение
Итак:
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 1633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.29 (0.027 с.) |



 предположим что
предположим что










 - экстремаль
- экстремаль

 , где:
, где:



 - Интегрант
- Интегрант - Терминант
- Терминант .
.


 – экстремаль
– экстремаль
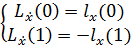 Посчитаем каждый элемент:
Посчитаем каждый элемент:





 .
.



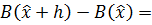 (Запишем, сразу группируя интегральную и неинтегральную части)
(Запишем, сразу группируя интегральную и неинтегральную части)
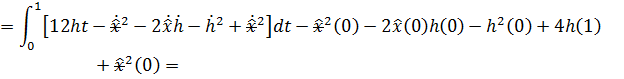
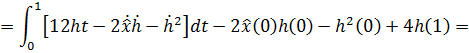
 и
и  в подстановке 0 и 1 (для подсчета значения элемента
в подстановке 0 и 1 (для подсчета значения элемента  ):
):  ,
, 


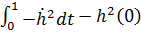 – отрицательный результат – следовательно
– отрицательный результат – следовательно  является точкой максимума.
является точкой максимума.

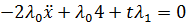
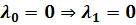 – нет решений (Лагранжиан не м. б. равен нулю)
– нет решений (Лагранжиан не м. б. равен нулю)




 ,
, 


 - Воспользуемся уравнением для нахождения
- Воспользуемся уравнением для нахождения  :
:







 ,
,  тоже должна быть равна нулю, следовательно
тоже должна быть равна нулю, следовательно 
 –
– 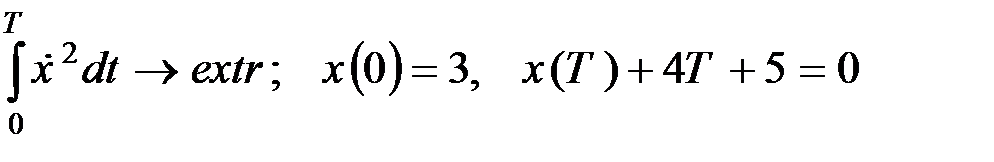




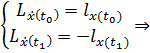
 Посчитаем каждый элемент:
Посчитаем каждый элемент:






 Тогда
Тогда 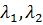 также равны нулю – нет решений.
также равны нулю – нет решений. , тогда:
, тогда:

 ,
, 



 , используя уравнение, написанное выше:
, используя уравнение, написанное выше:



 , тогда
, тогда  а
а  – что является недопустимым значением
– что является недопустимым значением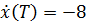 , тогда
, тогда  и
и 
 ,
, 
 ;
;  ,
, на предмет доставления функции максимума/минимума:
на предмет доставления функции максимума/минимума:

 Воспользуемся
Воспользуемся  из уравнения
из уравнения 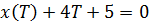 , помня, что
, помня, что  , а
, а 
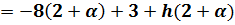



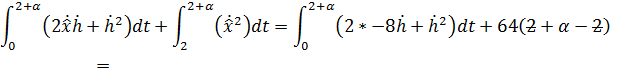



 – следовательно найденная точка является точкой минимума.
– следовательно найденная точка является точкой минимума.


