
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Окружность. Уравнение окружности.
Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке
Тогда из уравнения
(11.2)
Уравнению (11.2) удовлетворяют координаты любой точки Уравнение (11.2) называется каноническим уравнением окружности. В частности, полагая Уравнение окружности (11.2) после несложных преобразований примет вид 1) коэффициенты при 2) отсутствует член, содержащий произведение Рассмотрим обратную задачу. Положив в уравнении (11.1) значения
Преобразуем это уравнение:
т.е.
т.е.
Отсюда следует, что уравнение (11.3) определяет окружность при условии, Если
34.Эллипс (вершины, оси, полуоси, фокусы…).Уравнение эллипса. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
 и и  , расстояние между ними через , расстояние между ними через  , а сумму расстояний от произвольной точки эллипса до фокусов – через , а сумму расстояний от произвольной точки эллипса до фокусов – через  (см. рис. 49). По определению (см. рис. 49). По определению  , т.е. , т.е.  . .
Для вывода уравнения эллипса выберем систему координат Оху так, чтобы фокусы
Пусть
Это, по сути, и есть уравнение эллипса. Преобразуем уравнение (11.5) к более простому виду следующим образом:
 , то , то  . Положим . Положим
(11.6)
 или или
(11.7)
Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса. Эллипс – кривая второго порядка.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.2.122 (0.011 с.) |
 называется множество всех точек М плоскости, удовлетворяющих условию
называется множество всех точек М плоскости, удовлетворяющих условию  . Пусть точка М в прямоугольной системе координат Оху имеет координаты
. Пусть точка М в прямоугольной системе координат Оху имеет координаты  , а
, а  – произвольная точка окружности (см. рис. 48).
– произвольная точка окружности (см. рис. 48).



 и
и  , получим уравнение окружности с центром в начале координат
, получим уравнение окружности с центром в начале координат 
 При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:
При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия: и
и  равны между собой;
равны между собой; текущих координат
текущих координат и
и  получим
получим (11.3)
(11.3)

 (11.4)
(11.4) Ее центр находится в точке
Ее центр находится в точке 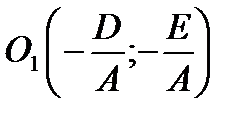 , а радиус
, а радиус  . Если же
. Если же  , то уравнение (11.3) имеет вид
, то уравнение (11.3) имеет вид 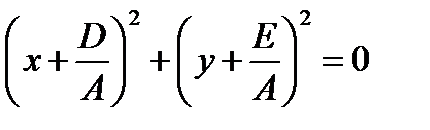 . Ему удовлетворяют координаты единственной точки
. Ему удовлетворяют координаты единственной точки  , то уравнение (11.4) а, следовательно, и равносильное уравнение (11.3) не определяет никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая часть – не отрицательна (говорят: «окружность мнимая»).
, то уравнение (11.4) а, следовательно, и равносильное уравнение (11.3) не определяет никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая часть – не отрицательна (говорят: «окружность мнимая»).


 . Тогда фокусы будут иметь следующие координаты
. Тогда фокусы будут иметь следующие координаты  , т.е.
, т.е. . (11.5)
. (11.5) ,
, ,
, ,
, ,
, .
. .
.
 .
.



