
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное уравнение прямой. Расстояние от точки до прямой.Стр 1 из 4Следующая ⇒
Нормальное уравнение прямой. Расстояние от точки до прямой. Нормальное уравнение прямой
Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде
 Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид
(10.11)
Покажем, как привести уравнение (10.4) прямой к виду (10.11). Умножим все члены уравнения (10.4) на некоторый множитель
Пример 10.2. Привести уравнение
Решение: Находим нормирующий множитель
Пусть заданы прямая L уравнением Решение: Расстояние d от точки
Так как точка
(10.13) что и требовалось получить.
Пример 10.3. Найти расстояние от точки
Решение: По формуле (10.13) получаем
Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Пусть прямые Требуется найти угол φ, на который надо повернуть в положительном направлении прямую
Решение: Имеем
 , поэтому , поэтому
(10.12)
откуда легко получим величину искомого угла.
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая – второй, то правая часть формулы (10.12) берется по модулю, т.е. Если прямые Если прямые
Асимптоты гиперболы Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой до этой прямой стремится к нулю при неограниченном удалении точки M
Покажем, что гипербола
Так как прямые (11.11) и гипербола (11.9) симметричны относительно координатных осей, то достаточно рассмотреть те точки указанных линий, которые расположены в первой четверти.
Возьмем на прямой
Как видно, по мере возрастания х знаменатель дроби увеличивается; числитель есть постоянная величина. Стало быть, длина отрезка MN стремится к нулю. Так как MN больше расстояния d от точки M до прямой, то d и подавно стремится к нулю. Итак, прямые

При построении гиперболы (11.9) целесообразно сначала построить основной прямоугольник гиперболы (см. рис. 57), провести прямые, проходящие через противоположные вершины этого прямоугольника, – асимптоты гиперболы и отметить вершины
Уравнение сферы
Найдем уравнение сферы радиуса R с центром в точке или
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере. Если центр сферы Если же дано уравнение Выражение «вообще говоря» означает, что в отдельных случаях уравнение Так, уравнению Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
Нормальное уравнение прямой. Расстояние от точки до прямой. Нормальное уравнение прямой
Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде
 Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид
(10.11)
Покажем, как привести уравнение (10.4) прямой к виду (10.11). Умножим все члены уравнения (10.4) на некоторый множитель
Пример 10.2. Привести уравнение
Решение: Находим нормирующий множитель
Пусть заданы прямая L уравнением Решение: Расстояние d от точки
Так как точка
(10.13) что и требовалось получить.
Пример 10.3. Найти расстояние от точки
Решение: По формуле (10.13) получаем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.150.89 (0.062 с.) |
 т.е.
т.е. 

 . Получим
. Получим  Это уравнение должно обратиться в (10.11). Следовательно, должны выполняться равенства:
Это уравнение должно обратиться в (10.11). Следовательно, должны выполняться равенства:  Из первых двух равенств находим
Из первых двух равенств находим  ,т.е.
,т.е. Множитель
Множитель  называется нормирующим множителем. Согласно третьему равенству
называется нормирующим множителем. Согласно третьему равенству 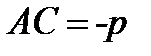 знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.
знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой. к нормальному виду.
к нормальному виду. Умножая данное уравнение на
Умножая данное уравнение на 
 О
О
 О
О
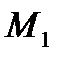 О
О
 О
О
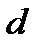 О
О
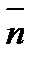 О
О
 О
О
 и точка
и точка  (см. рис. 47). Требуется найти расстояние от точки
(см. рис. 47). Требуется найти расстояние от точки 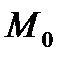 до прямой L.
до прямой L. до прямой L равно модулю проекции вектора
до прямой L равно модулю проекции вектора  , где
, где 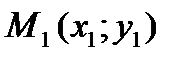 – произвольная точка прямой L, на направление нормального вектора
– произвольная точка прямой L, на направление нормального вектора  . Следовательно,
. Следовательно,


 принадлежит прямой L, то
принадлежит прямой L, то  , т.е.
, т.е. 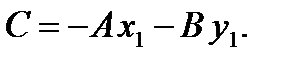 Поэтому
Поэтому до прямой
до прямой 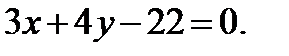

 и
и  заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами  и
и  (см. рис. 46).
(см. рис. 46).





 (теорема о внешнем угле треугольника) или
(теорема о внешнем угле треугольника) или  Если
Если  , то
, то 


 и
и 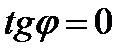 . Из формулы (10.12) следует
. Из формулы (10.12) следует  , т.е.
, т.е.  . И обратно, если прямые
. И обратно, если прямые  , то
, то  .
. . Следовательно,
. Следовательно,  . Отсюда
. Отсюда  , т.е.
, т.е.  (или
(или  ). Справедливо и обратное утверждение. Таким образом, условием перпендикулярности прямых является равенство
). Справедливо и обратное утверждение. Таким образом, условием перпендикулярности прямых является равенство 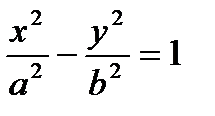 имеет две асимптоты:
имеет две асимптоты: и
и  . (11.11)
. (11.11)
 на гиперболе
на гиперболе  (см. рис. 56), и найдем разность MN между ординатами прямой и ветви гиперболы:
(см. рис. 56), и найдем разность MN между ординатами прямой и ветви гиперболы:


 являются асимптотами гиперболы (11.9).
являются асимптотами гиперболы (11.9). 



 и
и  гиперболы.
гиперболы. . Согласно определению сферы расстояние любой ее точки
. Согласно определению сферы расстояние любой ее точки  от центра
от центра  равен радиусу R, т.е.
равен радиусу R, т.е. 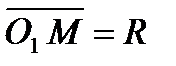 . Но
. Но  , где
, где  . Следовательно,
. Следовательно, 

 совпадает с началом координат, то уравнение сферы принимает вид
совпадает с началом координат, то уравнение сферы принимает вид 
 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.
, то оно, вообще говоря, определяет в пространстве некоторую поверхность. не удовлетворяют никакие действительные значения x, y и z. Уравнению
не удовлетворяют никакие действительные значения x, y и z. Уравнению  удовлетворяют лишь координаты точек, лежащих на оси Ox (из уравнения следует:
удовлетворяют лишь координаты точек, лежащих на оси Ox (из уравнения следует:  , а х – любое число)
, а х – любое число)


