
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайная величина распределена по нормальному закону, ее математическое ожидание равно 2, А дисперсия - 16. Тогда ее плотность распределения имеет вид ⇐ ПредыдущаяСтр 4 из 4
· Случайная величина распределена показательно с параметром · 1 Случайная величина Х имеет биномиальное распределение с параметрами · Случайная величина Х имеет биномиальное распределение с параметрами · Случайная величина Х имеет биномиальное распределение с параметрами · Случайная величина Х имеет биномиальное распределение с параметрами · Случайная величина Х имеет нормальное распределение с плотностью · 1;1 Случайная величина Х имеет нормальное распределение с плотностью распределения · 1; 36; 6 Случайная величина Х имеет показательное распределение с параметром · Случайная величина Х имеет распределение Коши с плотностью · -3; -3 Случайная величина Х имеет распределение Пуассона с параметром · Случайная величина Х имеет распределение Пуассона с параметром · Случайная величина Х называется нормированной, если · МХ = 0; DX =1 Случайная величина Х называется центрированной, если · МХ = 0 Случайная величина Х подчинена закону Пуассона с параметром соответственно · 3 Случайная величина Х равномерно распределена на · Случайная величина Х равномерно распределена на · Случайная величина Х распределена нормально с плотностью · 4; 4 Случайная величина Х распределена по биномиальному закону с параметрами · Случайная величина Х распределена по нормальному закону, ее математическое ожидание равно нулю, а среднеквадратическое отклонение равно 20. Плотность распределения Х имеет вид · Случайная величина Х распределена по нормальному закону, ее плотность вероятности
· 0; 9; 3 Случайная величина Х распределена по нормальному закону, ее плотность вероятности · Случайная величина Х распределена по нормальному закону. Известно, что математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид · Случайная величина Х распределена показательно с параметром · 1 Случайная величина Х распределена равномерно на · Случайная величина Х распределена равномерно, ее плотность равна · 1
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 2565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.61.16 (0.008 с.) |

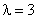 , тогда
, тогда 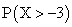 равна
равна тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы:
 тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы:
 Ее числовые характеристики таковы:
Ее числовые характеристики таковы:
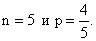 Тогда ее числовые характеристики равны
Тогда ее числовые характеристики равны
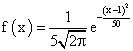 . Ее мода и медиана равны соответственно
. Ее мода и медиана равны соответственно . Тогда ее числовые характеристики МХ, DX и
. Тогда ее числовые характеристики МХ, DX и 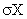 равны соответственно
равны соответственно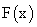 равна
равна
 тогда ее мода и медиана равны соответственно
тогда ее мода и медиана равны соответственно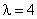 . Ее числовые характеристики равны
. Ее числовые характеристики равны
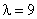 . Ее числовые характеристики равны
. Ее числовые характеристики равны
 , тогда ее математическое ожидание и дисперсия равны соответственно
, тогда ее математическое ожидание и дисперсия равны соответственно
 . Тогда вероятность попасть в интервал
. Тогда вероятность попасть в интервал  будет равна
будет равна
 ее мода и медиана равны соответственно
ее мода и медиана равны соответственно Ее числовые характеристики равны
Ее числовые характеристики равны

 . Тогда ее МХ, DX и
. Тогда ее МХ, DX и 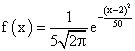 . Тогда ее числовые характеристики таковы:
. Тогда ее числовые характеристики таковы: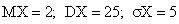
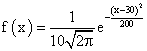
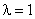 , тогда
, тогда 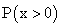 равна
равна , тогда вероятность попасть в интервал
, тогда вероятность попасть в интервал  равна
равна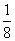
 Тогда параметр
Тогда параметр  равен
равен


