
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема № 1. Производная функции ⇐ ПредыдущаяСтр 2 из 2
Определение производной
Пусть функция Выполним следующие действия: - произвольной точке с координатой - вычислим значения функции - составим отношение
О
Рисунок 1
Определение производной. Если существует предел отношения
Операцию нахождения производной называют дифференцированием, а функцию, имеющую производную - дифференцируемой. Нижний индекс 0 выбран для удобства. Как очевидно, эта формула имеет место для любой точки Значение производной в точке
Операцию нахождения производной по определению называют непосредственным дифференцированием. На основании определения найдем производные от некоторых основных элементарных функций. Начнем со степенных функций. Примеры. Найти производные функций по определению. 1. Решение. Какую бы точку
Говорят, производная от константы равна нулю. 2. Решение. Функция определена на всей оси. Возьмем произвольную точку
Составим отношение
3. Решение. Функция определена на всей оси. Возьмем произвольную точку
Найдем предел отношения
Индекс 0 выбран для удобства, опуская его, можем записать
4. Решение. Функция определена на всей оси. Возьмем произвольную точку
Найдем предел отношения
Опуская индекс 0, можем записать
4. Продолжая увеличивать натуральную степень
Таким образом,
Данная формула остается справедливой для дробных и отрицательных степеней Например. 1) 2) Говорят, производная от корня квадратного равна дроби единица разделить на два таких корня.
5. Решение. Функция определена на всей оси. Возьмем произвольную точку
Найдем предел отношения
Здесь для раскрытия неопределенности
Таким образом, получили
5.
6. Решение. Функция определена на всей оси. Возьмем произвольную точку
Найдем предел отношения
Здесь для раскрытия неопределенности
Опуская индекс 0, можем записать
Говорят, производная от экспоненты равна этой же экспоненте.
7. Решение. Функция определена на полуоси
Найдем предел отношения
Здесь для раскрытия неопределенности Опуская индекс 0, можем записать
Прервемся пока на процедуре нахождения производной от основных элементарных функций по определению. Рассмотрим в чем состоит геометрический, механический и общефизический смысл производной, изучим свойства производной, которые называют правилами дифференцирования, определим производную от сложной и обратной функций и затем вернемся к нахождению производных от оставшихся основных элементарных функций которые занесем в таблицу и выучим наизусть.
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.145 (0.02 с.) |
 определена на интервале
определена на интервале  .
. придадим приращения
придадим приращения  , получим точку
, получим точку  ;
; в этих точках, и найдем соответствующее приращение функции, т.е.
в этих точках, и найдем соответствующее приращение функции, т.е.  (см. рис);
(см. рис); и найдем его предел при
и найдем его предел при  .
.











 то его называют производной функции
то его называют производной функции  ,
,  ,
,  ,
,  ,
, 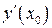 ,
,  ,
,  , т.е.
, т.е. .
.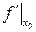 ,
,  .
. .
. , следовательно
, следовательно .
. .
. , где
, где  .
. , т.е.
, т.е.  .
. .
. .
. .
. .
. .
.
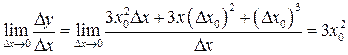 .
. .
. , находя предел отношения
, находя предел отношения  .
. .
. .
. .
. .
. .
.

 мы воспользовались эквивалентностью бесконечно малых функций, а именно
мы воспользовались эквивалентностью бесконечно малых функций, а именно 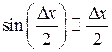 , при
, при  .
. .
. . Получить
. Получить  самостоятельно по аналогии.
самостоятельно по аналогии. .
.
 .
. , при
, при  .
. .
. .
. . Возьмем произвольную точку
. Возьмем произвольную точку  , придадим приращение
, придадим приращение  .
. .
.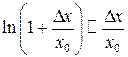 , при
, при  .
.


