
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монотонность функций. Экстремумы. ⇐ ПредыдущаяСтр 2 из 2
Наибольшее и наименьшее значения функции на отрезке
Функция f(x) называется возрастающей в точке х 0, если в некоторой e - окрестности этой точки f(x 0 -h)<f(x0)<f(x 0 +h). Убывающей – если f(x 0 +h)<f(x0)<f(x 0 -h), где 0< h <e. Функция f(x) называется возрастающей на отрезке [a,b], если для любых х 1 и х 2 этого отрезка из неравенства х 1> х 2следует неравенство f(х 1 ) > f(х 2 ). Если же из неравенства х 1> х 2следует, что f(х 1 ) < f(х 2 ), то функция f(x) – убывающая на отрезке [a,b]. Можно сформулировать достаточные признаки возрастания и убывания функции y=f(x) Если y' >0 для всех х Î[a,b], то функция возрастает на [a,b]; при y' <0 для х Î[a,b], то функция на [a,b] убывает. Функция f(x) может иметь экстремум лишь в тех точках, в которых f'(x) =0 или не существует. Такие точки называются критическими, или стационарными, или подозрительными на экстремум. Равенство нулю первой производной данной функции является необходимым условием существования экстремума. В качестве достаточного условия существования экстремума в критической точке х 0 можно принять смену знака первой производной при переходе через критическую точку, при этом, если знак меняется с + на -, то в точке х 0 – максимум, если с – на +, то в точке х 0 – минимум. Если производная y ' знак не меняет при переходе через точку, подозрительную на экстремум, то экстремума в этой точке нет. Для отыскания наибольшего и наименьшего значений функций у=f(x) на отрезке[a,b] необходимо найти критические точки, принадлежащие [a,b]. Вычислить значения функции в этих критических точках и на концах отрезка. Из всех найденных значений выбираем наибольшее и наименьшее. __________________
1.4.1. Найти интервалы монотонности следующих функций: а) у= 2-3 х + х 3; б) у=хе -х; в) у=(х -2 ) 2 (х+ 2 ); г) y=ln(x 2-2 x +4). Ответ: а) (-∞;-1)È(1;∞) – возрастает; (-1;1) – убывает; б) (-∞;1) – возрастает; (1;∞) – убывает; в) (-∞;-1)È(1;∞) – возрастает; (-1;1) – убывает; г) (-∞;1)– убывает; (1;∞) – возрастает; 1.4.2. Найти экстремумы функций: а) в) Ответ: а) у min= y( 0 )= 0; y max= б) у min= y( 0 )= 0; в) у max= y( 1 )= г) у min= y( 1 )= 0. 1.4.3. Найти наибольшее и наименьшее значения функций на заданном отрезке: а) у=х 4+2 х 2+5, х Î[-2,2]; б) в) Ответ: а) 29,5; б) 10; 6; в) 3/5; -1; г) у наиб=1.
_______________
1.4.4. Найти интервалы монотонности следующих функций: а) у=( 2 -х)(х+ 1 ) 2; б) у=х 3-6 х +5; в) у=х+е -х; г) y=xlnx. Ответ: а) (-∞;-1)È(1;∞) – убывает; (-1;1) – возрастает; б)(-∞;-2)È(2;∞) – возрастает; (-2;2) – убывает; в) (-∞;0) – возрастает; (0;∞) – убывает; г) (0;1/ е) – убывает; (1/ е;∞) – возрастает. 1.4.5. Найти экстремумы функций: а) Ответ: а) y max= y (11/4)=13/4; б) y min= y(e)=e. 1.4.6. Найти наибольшее и наименьшее значения функций на отрезке: а) в) Ответ: а) 8;0; б) 1; 3/5; в) π/4; 0.
Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты
Кривая называется выпуклой в точке х=х 0, если в некоторой окрестности этой точки кивая расположена под касательной, проведенной в этой точке (рис.6а), если же кривая лежит над касательной, то функция называется вогнутой (рис.6б).
В качестве достаточных условий выпуклости, вогнутости графика функций можно принять следующие: если y" >0, то кривая вогнутая, если y" <0, то кривая выпуклая. Точкой перегиба называется точка, разделяющая интервал выпуклости от интервала вогнутости. Необходимым условием существования точки перегиба является равенство нулю второй производной от функции, достаточным – изменение знака второй производной при переходе через точку, подозрительную на точку перегиба. Пусть имеется кривая, ветвь которой в том или ином направлении удаляется в бесконечность. Если расстояние от точки кривой до некоторой прямой по мере удаления точки кривой в бесконечность стремится к нулю, то эта прямая называется асимптотой графика кривой. Существует три вида асимптот: вертикальная, горизонтальная, наклонная. Пусть y=f(x), а – точка разрыва функции или граничная точка области определения. Если Если Наклонная асимптота имеет вид у=kx+b, где Замечание. Пределы при х ®∞, х ®-∞ находятся отдельно.
Алгоритм полного исследования функции y=f(x)
1. Найти область определения функции; точки разрыва. 2. Найти асимптоты графика функции.
3. Определить четность, нечетность, периодичность функции. 4. Установить промежутки возрастания, убывания и экстремумы функции. 5. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции. 6. Найти точки пересечения графика с осями координат. 7. При необходимости вычислить значения функции в дополнительных точках. ___________________
1.5.1. Найти промежутки выпуклости, вогнутости, точки перегиба: а) у=х 5-5 х -6; б) у=(х- 5 ) 5/3+2; в) у=хе х; г) у=х 4-8 х 3+24 х 2. Ответ: а) (-∞;0) – выпуклая; (0;∞) – вогнутая; б) р(5;2) – точка перегиба; в) (-∞;-2) – выпуклая; (-2;∞) – вогнутая; г) точек перегиба нет. 1.5.2. Найти асимптоты графика функций: а) в) Ответ: а) х =-2, у =3; б) х =1, х = -6, у =0; в) у=х -6; г) 1.5.3. Исследовать функции и построить их графики: а) в) Ответ: а) у min(2)=3; асимптоты у = х, х =0; б) у min(2Ö3)=3Ö3, у max(-2Ö3)= -3Ö3; (0;0) – точка перегиба; х =±2, у=х – асимптоты; в) у max(е 2)=2/ е, у =0 – асимптоты; г) у max(1)= е. 1.5.4. Найти промежутки выпуклости, вогнутости, точки перегиба: а) в) y=ln|x|; г) Ответ: а) (2;-8/3); б) г) 1.5.5. Найти асимптоты графиков функций: а) в) Ответ: а) х= 0; у =1; б) 1.5.6. Исследовать функции и построить графики: а) Ответ: а) у=-х – наклонная асимптота; б) у min(6)=13,5; (0;0) – точка перегиба; х =2; у = х +4 – асимптоты.
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 880; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.124.252 (0.018 с.) |
 ; б) y=ln(x 2+1 );
; б) y=ln(x 2+1 ); ; г) у=(х- 1 ) 6/7.
; г) у=(х- 1 ) 6/7. ;
;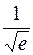 ; y min=
; y min=  ;
; , х Î[-6,8];
, х Î[-6,8];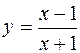 , х Î[0,4]; г) y =2 tgx-tg 2 x, х Î[0,π/2].
, х Î[0,4]; г) y =2 tgx-tg 2 x, х Î[0,π/2]. ; б)
; б)  .
. , х Î[0,4]; б)
, х Î[0,4]; б)  , х Î[0,1];
, х Î[0,1]; , х Î[0,1].
, х Î[0,1].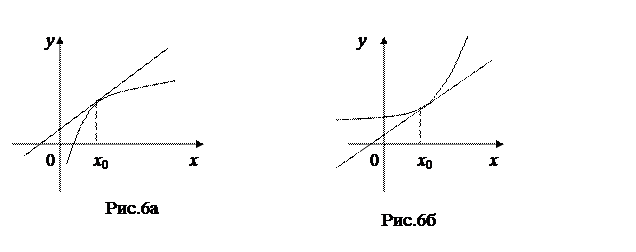
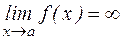 , то прямая х=а есть вертикальная асимптота.
, то прямая х=а есть вертикальная асимптота.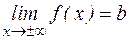 , то прямая х=b – горизонтальная асимптота.
, то прямая х=b – горизонтальная асимптота.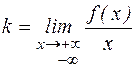 ;
; 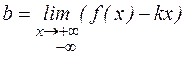 .
.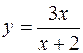 ; б)
; б) 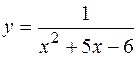 ;
; ; г) y=-xarctgx.
; г) y=-xarctgx.
 ; б)
; б) 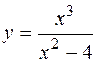 ;
;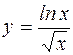 ; г)
; г) 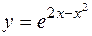 .
. ; б)
; б)  ;
;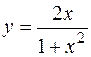 .
.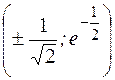 ; в) точек перегиба нет;
; в) точек перегиба нет;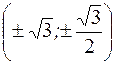 .
.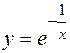 ; б) y=x-arctgx;
; б) y=x-arctgx;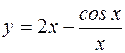 .
.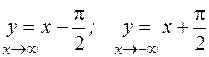 ; в) у= 2 х; х =0.
; в) у= 2 х; х =0.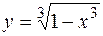 ; б)
; б) 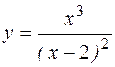 .
.


