Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Дифференцирование функцийСтр 1 из 2Следующая ⇒
МАТЕМАТИКА Дифференциальное исчисление функций одной и нескольких переменных
Методические указания и задачи к практическим занятиям для студентов I курса очной формы обучения инженерно-технических специальностей (II семестр)
Брянск 2011 УДК 511 Математика. Дифференциальные исчисления функций одной и нескольких переменных [Текст]+[Электронный ресурс]: методические указания и задачи к практическим занятиям для студентов I курса очной формы обучения инженерно-технических специальностей (II семестр). – Брянск: БГТУ. - 28с.
Разработали: доц. Ольшевская Н.А. доц. Цуленева Г.Г. асс. Сенько К.А.
Рекомендовано кафедрой «Высшая математика» (протокол №2 от 18.10.11).
Научный редактор Гореленков А.И. Редактор издательства Королева Т.И. Компьютерный набор Левкина А.П.
Темплан 2011 г., п. 226 Подписано в печать 18.11.11. Формат 60х84 1/16 Бумага офсетная Офсетная печать. Печ. л. 1,63 Уч.-изд. л. 1,63 Т. 30 экз. Заказ Бесплатно Издательство Брянского государственного технического университета Брянск, бульвар 50-летия Октября, 7, тел. 588-249 Лаборатория оперативной печати БГТУ, ул. Институтская, 16
ПРЕДИСЛОВИЕ
Настоящие методические указания ориентированы на студентов I курса очной формыобучения инженерно-технических специальностей. В методических указаниях приводятся необходимые для практических занятий теоретические сведения и большое количество примеров и задач различного уровня сложности для аудиторной и самостоятельной работы студентов. Все задания снабжены ответами. Методические указания и подобранные задачи должны помочь студентам освоить программу курса и приобрести устойчивые практические навыки решения задач.
ОГЛАВЛЕНИЕ
Предисловие……………………………………………………………3 Глава 1 Дифференцирование функций………………………………5 1.1 Основные правила дифференцирования….……..………5 1.2. Уравнения касательной и нормали к плоской кривой……………………………………………8 1.3. Производные высших порядков. Правила Лапиталя………………………………………….9 1.4. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке…………………………………….….11 1.5. Промежутки выпуклости,
вогнутости графика функции. Точки перегиба. Асимптоты………………….……………14 1.6. Параметрически заданные функции. Векторная функция скалярного аргумента. Кривизна плоской кривой………………..……….……….17 Глава 2. Функции нескольких переменных…………………………18 2.1. Понятие функции нескольких переменных…………..…18 2.2. Частные производные первого порядка. Полный дифференциал……………………………….….20 2.3. Дифференцирование сложных и неявных функций……22 2.4. Касательная плоскость и нормаль к поверхности……..24 2.5. Производная по направлению. Градиент……………….25 2.6. Экстремум функции двух переменных………………….27 Список рекомендуемой литературы…………………………………..28 Глава 1. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ Производные высших порядков. Правила Лопиталя
Пусть дана функция y=f(x); производная от этой функции y′=f′(x). Производная от этой производной называется производной второго порядка функции y=f(x), которая обозначается как y" или f"(x) = Аналогично определяются производные более высокого порядка f(n)(x) = Правила Лопиталя Первое правило. Неопределенность Если Второе правило. Неопределенность Если Неопределенности вида 0∞; ∞-∞; 1∞;00 сводятся к неопределенностям ______________
1.3.1. Найти производные второго порядка: а) y=cos 2 x; б) y=arctgx 2 ;в) г) 1.3.2. Найти f' (0), f "(0), f "'(0) если f(x)=e 2x sin 3 x. 1.3.3. Вывести формулу для производной n – го порядка для функций: а) y=xm; б) у=ах. Ответ: а) у(n)=m(m- 1 )…(m-n+ 1 )xm-n. б) y(n)=ax(lna)n. 1.3.4. Найти пределы: а) в) д) ж) и) Ответ: а) _________________
1.3.5. Найти производные второго порядка: а) у=(х 2-10 х +5 ) 5; б) y=sin2x; в) 1.3.6. Найти выражение для n -й производной следующих функций: а) у =3х; б) у = cosx; в) y=sin 2 x. 1.3.7. Найти пределы: а) в) д) ж) и) Ответ: а) 1; б) 0; в)0; г)10; д) -1/3; е)∞; ж) -1; з) 1; и) 1; к)1.
Точки перегиба. Асимптоты
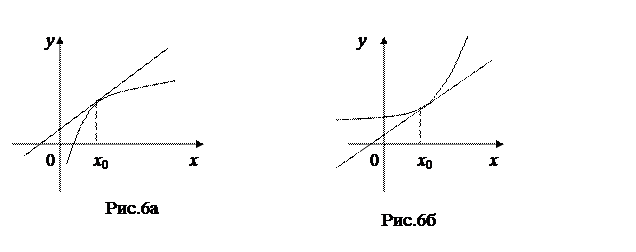
Кривая называется выпуклой в точке х=х 0, если в некоторой окрестности этой точки кивая расположена под касательной, проведенной в этой точке (рис.6а), если же кривая лежит над касательной, то функция называется вогнутой (рис.6б).
В качестве достаточных условий выпуклости, вогнутости графика функций можно принять следующие: если y" >0, то кривая вогнутая, если y" <0, то кривая выпуклая. Точкой перегиба называется точка, разделяющая интервал выпуклости от интервала вогнутости. Необходимым условием существования точки перегиба является равенство нулю второй производной от функции, достаточным – изменение знака второй производной при переходе через точку, подозрительную на точку перегиба. Пусть имеется кривая, ветвь которой в том или ином направлении удаляется в бесконечность. Если расстояние от точки кривой до некоторой прямой по мере удаления точки кривой в бесконечность стремится к нулю, то эта прямая называется асимптотой графика кривой. Существует три вида асимптот: вертикальная, горизонтальная, наклонная. Пусть y=f(x), а – точка разрыва функции или граничная точка области определения. Если Если Наклонная асимптота имеет вид у=kx+b, где Замечание. Пределы при х ®∞, х ®-∞ находятся отдельно.
Алгоритм полного исследования функции y=f(x)
1. Найти область определения функции; точки разрыва. 2. Найти асимптоты графика функции. 3. Определить четность, нечетность, периодичность функции. 4. Установить промежутки возрастания, убывания и экстремумы функции. 5. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции. 6. Найти точки пересечения графика с осями координат. 7. При необходимости вычислить значения функции в дополнительных точках. ___________________
1.5.1. Найти промежутки выпуклости, вогнутости, точки перегиба: а) у=х 5-5 х -6; б) у=(х- 5 ) 5/3+2; в) у=хе х; г) у=х 4-8 х 3+24 х 2. Ответ: а) (-∞;0) – выпуклая; (0;∞) – вогнутая; б) р(5;2) – точка перегиба; в) (-∞;-2) – выпуклая; (-2;∞) – вогнутая; г) точек перегиба нет. 1.5.2. Найти асимптоты графика функций: а) в) Ответ: а) х =-2, у =3; б) х =1, х = -6, у =0; в) у=х -6; г) 1.5.3. Исследовать функции и построить их графики: а) в) Ответ: а) у min(2)=3; асимптоты у = х, х =0; б) у min(2Ö3)=3Ö3, у max(-2Ö3)= -3Ö3; (0;0) – точка перегиба; х =±2, у=х – асимптоты; в) у max(е 2)=2/ е, у =0 – асимптоты; г) у max(1)= е. 1.5.4. Найти промежутки выпуклости, вогнутости, точки перегиба: а) в) y=ln|x|; г) Ответ: а) (2;-8/3); б) г) 1.5.5. Найти асимптоты графиков функций: а) в) Ответ: а) х= 0; у =1; б) 1.5.6. Исследовать функции и построить графики: а) Ответ: а) у=-х – наклонная асимптота; б) у min(6)=13,5; (0;0) – точка перегиба; х =2; у = х +4 – асимптоты.
Кривизна плоской кривой
Пусть даны две функции переменной величины Если Пусть теперь некоторая кривая задана в пространстве R3своими параметрическими уравнениями:
Если
Пусть задана плоская кривая уравнением y=f(x). Величина Радиус кривизны есть ________________
1.6.1. Найти Ответ: 1.6.2. Исключить параметр t из уравнений x=acost, y=bsint. Построить кривую. Ответ: 1.6.3. Траектория движения материальной точки задана уравнением Ответ: 1.6.4. Определить кривизну кривой Ответ:
Полный дифференциал
Производная функции z=F(x,y) по х, найденная в предположении, что у остается постоянным, называется частной производной z по х и обозначается Аналогично определяется и обозначается частная производная z по у:
Тогда выражение ____________________________
Найти частные производные функций:
Найти полные дифференциалы функций:
Ответы: 1. 2. 3. 5. 7. 9.
12.
14. 16. 17.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. Письменный, Д.Т. Конспект лекций по высшей математике/ Д.Т. Письменный. – 6-е изд. – М.: Айрис-пресс, 2006-288с. 2. Минорский, В.П., Сборник задач по высшей математике: учеб.пособ. для втузов/ В.П. Минорский. – М.:Физ.мат.лит., 2004.
Дополнительная
1. Данко, П.Е. Высшая математика в упражнениях и задачах/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Оникс 21 век, Мир и образование, 2005 – 242с. 2. Лунку, К.Н. Сборник задач по высшей математике/ К.Е. Лунку. – М.: Айрис-пресс, 2009 – 592с.
МАТЕМАТИКА Дифференциальное исчисление функций одной и нескольких переменных
Методические указания и задачи к практическим занятиям для студентов I курса очной формы обучения инженерно-технических специальностей (II семестр)
Брянск 2011 УДК 511 Математика. Дифференциальные исчисления функций одной и нескольких переменных [Текст]+[Электронный ресурс]: методические указания и задачи к практическим занятиям для студентов I курса очной формы обучения инженерно-технических специальностей (II семестр). – Брянск: БГТУ. - 28с.
Разработали: доц. Ольшевская Н.А. доц. Цуленева Г.Г. асс. Сенько К.А.
Рекомендовано кафедрой «Высшая математика» (протокол №2 от 18.10.11).
Научный редактор Гореленков А.И. Редактор издательства Королева Т.И. Компьютерный набор Левкина А.П.
Темплан 2011 г., п. 226 Подписано в печать 18.11.11. Формат 60х84 1/16 Бумага офсетная Офсетная печать. Печ. л. 1,63 Уч.-изд. л. 1,63 Т. 30 экз. Заказ Бесплатно Издательство Брянского государственного технического университета Брянск, бульвар 50-летия Октября, 7, тел. 588-249 Лаборатория оперативной печати БГТУ, ул. Институтская, 16
ПРЕДИСЛОВИЕ
Настоящие методические указания ориентированы на студентов I курса очной формыобучения инженерно-технических специальностей. В методических указаниях приводятся необходимые для практических занятий теоретические сведения и большое количество примеров и задач различного уровня сложности для аудиторной и самостоятельной работы студентов. Все задания снабжены ответами. Методические указания и подобранные задачи должны помочь студентам освоить программу курса и приобрести устойчивые практические навыки решения задач.
ОГЛАВЛЕНИЕ
Предисловие……………………………………………………………3 Глава 1 Дифференцирование функций………………………………5 1.1 Основные правила дифференцирования….……..………5 1.2. Уравнения касательной и нормали к плоской кривой……………………………………………8 1.3. Производные высших порядков. Правила Лапиталя………………………………………….9 1.4. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке…………………………………….….11 1.5. Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты………………….……………14 1.6. Параметрически заданные функции. Векторная функция скалярного аргумента. Кривизна плоской кривой………………..……….……….17 Глава 2. Функции нескольких переменных…………………………18 2.1. Понятие функции нескольких переменных…………..…18 2.2. Частные производные первого порядка. Полный дифференциал……………………………….….20 2.3. Дифференцирование сложных и неявных функций……22 2.4. Касательная плоскость и нормаль к поверхности……..24 2.5. Производная по направлению. Градиент……………….25 2.6. Экстремум функции двух переменных………………….27 Список рекомендуемой литературы…………………………………..28 Глава 1. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.43.119 (0.15 с.) |
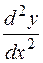 .
. .
. .
.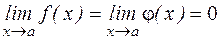 , то
, то 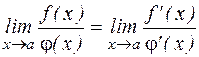 .
.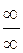 .
.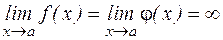 , то
, то 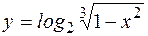 ;
; ; д)
; д) 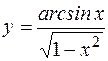 .
.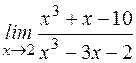 ; б)
; б)  ;
;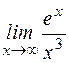 ; г)
; г) 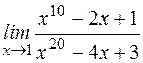 ;
;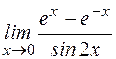 ; е)
; е) 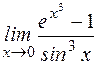 ;
;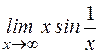 ; з)
; з)  ;
; ; к)
; к)  .
.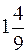 ; б) 1; в) ∞; г) 1/2; д) 1; е)1; ж) 1; з)0; и) 1; к)1.
; б) 1; в) ∞; г) 1/2; д) 1; е)1; ж) 1; з)0; и) 1; к)1.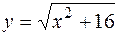 ; г) у=ln(x 3-2 x 2+4).
; г) у=ln(x 3-2 x 2+4).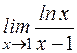 ; б)
; б)  ;
;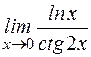 ; г)
; г)  ;
; ; е)
; е) 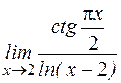 ;
;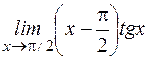 ; з)
; з)  ;
;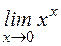 ; к)
; к) 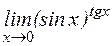 .
.
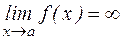 , то прямая х=а есть вертикальная асимптота.
, то прямая х=а есть вертикальная асимптота.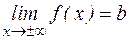 , то прямая х=b – горизонтальная асимптота.
, то прямая х=b – горизонтальная асимптота.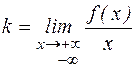 ;
; 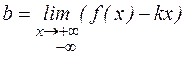 .
.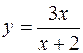 ; б)
; б) 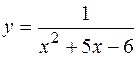 ;
; ; г) y=-xarctgx.
; г) y=-xarctgx.
 ; б)
; б) 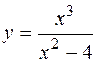 ;
;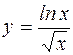 ; г)
; г) 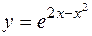 .
. ; б)
; б) 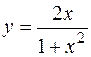 .
.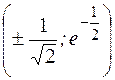 ; в) точек перегиба нет;
; в) точек перегиба нет;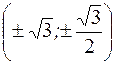 .
.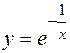 ; б) y=x-arctgx;
; б) y=x-arctgx;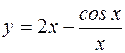 .
.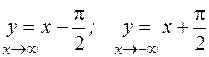 ; в) у= 2 х; х =0.
; в) у= 2 х; х =0.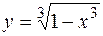 ; б)
; б) 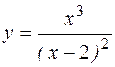 .
.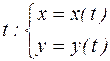 , рассматриваемые для одних и тех же значений t. Эти уравнения на плоскости задают некоторую кривую. Так как переменная t называется параметром, то и приведенная система называется параметрическимуравнениемкривой.
, рассматриваемые для одних и тех же значений t. Эти уравнения на плоскости задают некоторую кривую. Так как переменная t называется параметром, то и приведенная система называется параметрическимуравнениемкривой.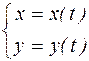 , то
, то 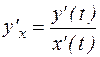 , а
, а 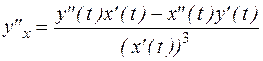 .
. . Тогда каждому значению t можно поставить в соответствие вектор
. Тогда каждому значению t можно поставить в соответствие вектор 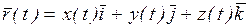 , который называется векторной функцией скалярного аргумента t. Линия с, описываемая концом радиуса – вектора
, который называется векторной функцией скалярного аргумента t. Линия с, описываемая концом радиуса – вектора  , называется годографом.
, называется годографом.
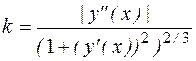 определяет ее кривизну.
определяет ее кривизну.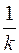 . Для параметрически заданной кривой
. Для параметрически заданной кривой 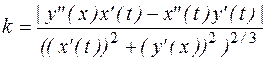 .
.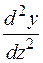 , если x=arccost, y=arcsint.
, если x=arccost, y=arcsint.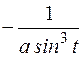 .
.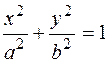 .
.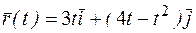 . Найти закон изменения скорости движения. Построить траекторию и векторы скорости при t =0; t =1.
. Найти закон изменения скорости движения. Построить траекторию и векторы скорости при t =0; t =1.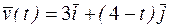 .
.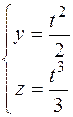 при t =1.
при t =1.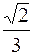 .
.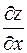 или F ' x(x,y).
или F ' x(x,y).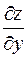 или F ' у(x,y). Если функция z=F(x,y) имеет в точке (х,у) непрерывные частные производные, то ее полное приращение может быть представлено в виде
или F ' у(x,y). Если функция z=F(x,y) имеет в точке (х,у) непрерывные частные производные, то ее полное приращение может быть представлено в виде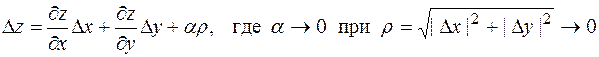 .
.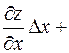
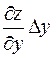 есть главная часть полного приращения
есть главная часть полного приращения 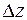 ; она называется полным дифференциалом функции и обозначается dz:
; она называется полным дифференциалом функции и обозначается dz: 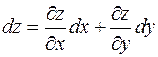 , (здесь dx= D x, dy= D y – произвольные приращения аргументов).
, (здесь dx= D x, dy= D y – произвольные приращения аргументов).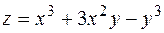 .
.
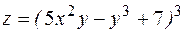 .
.
 .
.
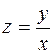 .
.
 .
.
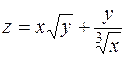 .
.
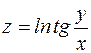 .
.
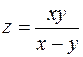 .
.
 .
.
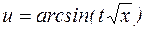 .
.
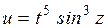 .
.
 .
.
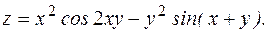
 .
.
 .
.
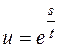 .
.
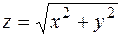 .
.
 .
.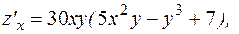
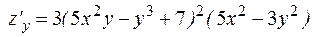 .
. . 4.
. 4. 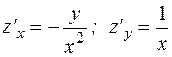 .
.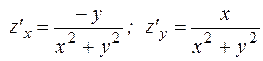 . 6.
. 6.  .
.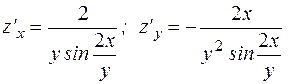 . 8.
. 8. 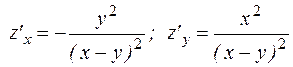 .
.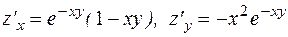 . 10.
. 10.  ;
;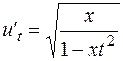 . 11.
. 11. 
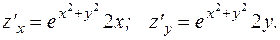 13.
13. 
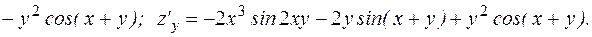
 15.
15. 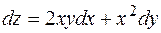 .
.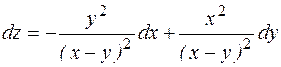 .
. . 18.
. 18.