В програмній системі algo 2000

 

Мета роботи – розробка алгоритмів функціонування МТ для виконання простих функцій за допомогою програмного інтерпретатора ALGO 2000.

 

Завдання для виконання лабораторної роботи

 

1Розробити МТ, яка б виконувала операцію (x div 2) і мала вхідний алфавіт А = {0, 1, ε}, де символ ε – це пустий символ (пробіл).

Операція (x div 2) реалізується зсувом ланцюжка вправо на один розряд.

2 Розробити МТ, яка б виконувала операцію конкатенації двох ланцюжків, заданих у вхідному алфавіті А = {0, 1, *, ε}.

3 Розробити МТ, яка б виконувала операцію копіювання вхідного ланцюжка, заданого в алфавіті А = {1, *, ε}, де символ «*» використовується в якості розділювача двох ланцюжків.

4 Розробити МТ, яка б виконувала множення числа в десятковій системі числення на 11.

5 Розробити МТ, яка б знаходила додаток числа в десятковій системі числення та числа в трійковій системі числення, наприклад, 576+100. Додаток треба подати в десятковій системі числення. Каретка розташована на крайній правій цифрі правого числа.

Розробити МТ, яка б могла виступати як двійково–вісімковий дешифратор.

7 Розробити МТ, яка б установлювала співвідношення між двома натуральними числами: m та n, які представлено в унарній системі числення. Між числами m та n стоїть знак «?», який замінюють залежно від співвідношення між числами на один з підходящих знаків «>», «<», «=».

 

ЗАГАЛЬНІ ПОЛОЖЕННЯ

 

Твердять, що МТ обчислює функцію f(x₁, x₂,..., x_n), якщо виконуються наступні умови:

1) для будь–яких x₁, x₂,..., x_n, які належать до області визначення функції, МТ з початкової конфігурації, маючи на стрічці подання аргументів, переходить у заключну конфігурацію, маючи на стрічці результат (подання функції);2) для будь–яких x₁, x₂,..., x_n, які не належать до області визначення функції, МТ, починаючи з початкової конфігурації, працює нескінченно.

Якщо початкова та заключна конфігурації МТ є стандартними, то говорять, що МТ правильно обчислює функцію.

Функція називається обчислюваною за Тьюрингом, якщо існує машина Тьюринга, що обчислює її.

Для доведення обчислювальності функції, а надалі й існування алгоритму, необхідно побудувати МТ, реалізація якої на практиці найчастіше являє собою трудомістке завдання. У зв'язку з цим виникає необхідність розбиття алгоритму на окремі задачі, кожна з яких буде розв’язуватись окремою машиною Тьюринга. Якщо об'єднати програми цих машин, то вийде нова програма, яка буде дозволяти вирішувати вихідну задачу.

Машини Тюринга можуть обчислювати шукану функцію з відновленням і без відновлення. Обчислення функції з відновленням означає, що машини Тьюринга працюють із збереженням початкових даних: спочатку отримати результат на стрічці, а потім початкові дані. Обчислення функції без відновлення означає, що машини Тьюринга працюють без збереження початкових даних.

Справедливим є твердження про те, що будь–яка правильно обчислювана функція є правильно обчислюваною, якщо вона обчислюється з відновленням.

Обчислювана функція використовується для уточнення поняття алгоритму.

Обчислювальна функція це будь–яка числова функція (зазвичай від цілочислових аргументів та з цілочисловою областю значень), значення якої може бути обраховане за допомогою деякого алгоритму.

Математично точно описана множина числових функцій, які співпадають з сукупністю всіх обчислювальних функцій з широким розумінням алгоритму, отримала назву рекурсивних функцій.

Тезис Черча формулюється наступним чином: клас усіх рекурсивних функцій співпадає з класом скрізь визначених обчислювальних функцій.

Порядок виконання лабораторної роботи

Приклад 1

Побудувати машину Тьюринга, яка правильно обчислює функцію f(x) = x+1 за правилами двійкового додавання.

1.1 Обрати вхідний алфавіт А ={0, 1, ε}, де ε – пустий символ (пробіл).

1.2 Представити МТ у вигляді таблиці відповідності (рис. 32)

 

 

Рисунок 32 – Уведені дані

 

1.3 Записати програму побудованої МТ для випадку, коли вхідний ланцюжок на стрічці дорівнює двійковому числу 111. Зліва від кожної команди наведено представлення вхідного ланцюжка на стрічці до виконання даної команди. Символ, який знаходиться під головкою, будемо позначати підкресленням.

Так як на стрічці написано число 111, то команди з цифрою 0 не використовуються.

1) q₀1 → q₀1R ε 1 11ε (в початковому стані q₀ головка знаходиться на першій клітинці з цифрою 1 та згідно з командою не змінює вмісту клітинки, а тільки переміщується вправо);

2) q₀1 → q₀1R ε1 1 1ε (стан q₀ не змінюється і головка далі переміщується вправо на наступну клітинку з цифрою 1);

3) q₀1 → q₀1R ε11 1 ε (стан q₀ не змінюється і головка далі переміщується вправо на наступну клітинку з цифрою 1);

4) q₀ε → q₁εL ε111 ε (стан q₀ змінюється, всі одиниці числа на інформаційній стрічці закінчилися, а отже головка зустрічає символ ε (пуста клітинка), переходить в стан q₁, згідно з яким головка зміщується вліво, при цьому в клітинці зліва повинна виконатися заміна установленої цифри 1 на цифру 0, що демонструюють пункти 5 і 6);

5) q₁1 → q₁0L ε11 1 ε;

6) q₁1 → q₁0L ε11 0 ε;

7) q₁1 → q₁0L ε1 0 0ε (в подальшому виконується така ж сама команда і залишається такий самий стан: стан q₁, заміна цифри 1 на цифру 0 і переміщення головки вліво);

8) q₁1 → q₁0L ε 0 00ε (в подальшому виконується така ж сама команда і залишається такий самий стан: стан q₁, заміна цифри 1 на цифру 0 і переміщення головки вліво);

9) q₁ε → q₂1L ε 000ε (стан q₁ змінюється, виконана заміна всіх трьох цифр 1 на цифру 0, а отже головка зустрічає символ ε, переходить в стан q₂, згідно з яким головка переміщується вліво та замінює символ ε на цифру 1);

10) q₂ ε → q_к εR ε 1000ε.

Із прикладу видно, що МТ із стандартної початкової конфігурації, маючи на стрічці число 111, після виконання сукупності команд (п.п. 1-10) перейшла в стандартний заключний стан, маючи на стрічці результат 1000. Дійсно 111₂ + 1₂ = 1000₂.

Результат роботи МТ наведено на рисунку 33.

 

 

Рисунок 33 – Результат роботи функції f(x) = x+1

 

1.4 Увести двійкове число 1001111.

Отриманий результат є наступний:

 

Приклад 2

Написати програму, яка б розв’язувала задачу «подільності на 4».

У процесі стандартного кодування ціле число n представляється словом з нулей та одиниць, тобто двійковим записом даного числа. Додатне ціле число ділиться на 4 тоді і тільки тоді, коли дві останні цифри двійкового запису даного числа є нулями.

2.1 Обрати вхідний алфавіт А ={0, 1}.

2.2 Представити МТ у вигляді таблиці відповідності (рис. 34).

 

 

Рисунок 34 – МТ для розв’язання задачі «подільності на 4»

 

Розроблена програма обчислює функцію , яка відображає кожне слово в слово f_M(x), яке отримується з х знищенням двох крайніх справа символів. Якщо , то програма в якості f_M(x) видає пусте слово.

На рисунку 35 наведено демонстрацію роботи алгоритму програми для розв’язання задачі «подільності на 4» числа х=10100, яке в десятковій системі числення є числом 20.

 

Рисунок 35 – Візуалізація роботи наведеної програми

 

2.3 Запустити програму для виконання. Отриманий результат наведено на рисунку 36.

 

 

Рисунок 36 – Результат роботи програми «подільності на 4»

 

У десятковій системі числення число 101 відповідає числу 5.

Наведена програма видалила з уведеного числа дві останні цифри – нулі, тим самим підтверджуючи подільность введеного числа на 4.

У випадку, якщо двома останніми цифрами уведеного числа є не нулі, програма не вносить жодних змін, а це означає, що введене число є неподільним на 4.

2.4 Запустити програму для виконання, якщо введеное число є 1010000, що відповідає числу 80 в десятковій системі числення. Перевірити правильність роботи програми.

2.5 Запустити програму для виконання, якщо введене число є 1010011, що відповідає числу 83 в десятковій системі числення. Перевірити правильність роботи програми.

 

Приклад 3 Розробити машину Тьюринга, яка б збільшувала на 1 задане в вісімковій системі числення число n.

Вісімкова система числення – це позиційна цілочисельна система числення з основою 8. Для представлення чисел в ній використовуються цифри від 0 до 7.

Вісімкова система найчастіше використовується в областях, пов’язаних із цифровими пристроями, та характеризується легким переведенням вісімкових чисел у двійкові і назад шляхом заміни вісімкових чисел на триплети двійкових. Ця система числення раніше широко використовувалася в програмуванні і взагалі в комп’ютерній документації, проте в даний час майже повністю витіснена шістнадцятиричною системою.

3.1 Задати зовнішній алфавіт у вигляді послідовності цифр: 0 1 2 3 4 5 6 7.

3.2 Заповнити таблицю МТ командами, як це наведено на рисунку 37.

 

 

Рисунок 37 – Обчислення в вісімковій системі

 

Автомат у стані q₀ оглядає будь–яку цифру вхідного слова відповідно до команд першого стовпчика.

Команди другого стовпчика додають одиницю до потрібної цифри (тієї, що введена на інформаційну стрічку) та виконують зупинення програми.

Результат роботи програми наведено на рисунку 38.

 

 

Рисунок 38 – Результат обчислення в вісімковій системі

 

Розроблена програма збільшує розрядність введеного числа відповідно до правил математики.

Приклад 4

Написати програму, яка б моделювала роботу МТ, що збільшує задане десяткове число на 2. При цьому головка повинна бути розташована на першій цифрі числа.

4.1 Задати зовнішній алфавіт у вигляді послідовності цифр: 0 1 2 3 4 5 6 7 8 9.

4.2 Заповнити таблицю МТ командами, як це наведено на рисунку 39.

 

 

Рисунок 39 – Робота з десятковим числом

 

Команди першого стовпчика призначено для перегляду окремо заданої на інформаційній стрічці цифри та переміщення головки вправо до наступної цифри. За досягнення кінця послідовності та переходу до першої пустої клітинки виконується переміщення вліво відповідно до послідовності за допомогою команди _ q₁.

Команди другого стовпчика виконують додавання цифри 2 до кожної з проглянутих цифр, при цьому додавання цифри 2 до цифри 8 приведе до заповнення клітинки 0, а додавання цифри 2 до цифри 9 – до заповнення клітинки 1.

Результат роботи програми наведено на рисунку 40.

 

Рисунок 40 – Результат роботи програми

 

Приклад 5 Розробити МТ, яка б змогла записане в десятковій системі числення число множити на 2. При цьому головка розташована над лівою цифрою, тобто автомат у стані q₀ оглядає крайню ліву цифру числа (але головка може знаходитися й над крайньою правою клітинкою)

5.1 Задати зовнішній алфавіт у вигляді послідовності цифр: 0 1 2 3 4 5 6 7 8 9.

5.2 Заповнити таблицю МТ командами, як це наведено на рисунку 41.

 

Рисунок 41 – Програма множення на 2 числа, записаного в десятковій системі числення

 

У даній програмі:

– стан q₀ служить для виконання команд пошуку правої (молодшої) цифри числа;

– стан q₁ служить для виконання команд множення чергової цифри числа на 2 без додавання одного переносу;

– стан q₂ служить для виконання команд множення чергової цифри числа на 2 з додаванням одного переносу.

Результат роботи програми наведено на рисунку 42.

 

Рисунок 42 – Результат виконання програми множення на 2 числа, записаного в десятковій системі числення

 

Приклад 6 Розробити МТ, яка б зменшувала на одиницю задане натуральне число n, що є більшим за 1. При цьому в вихідному слові старша цифра не повинна дорівнювати 0. Головка знаходиться над лівою цифрою.

6.1 Задати зовнішній алфавіт у вигляді наступної послідовності цифр: 0 1 2 3 4 5 6 7 8 9.

6.2 Заповнити таблицю МТ командами, як це наведено на рисунку 43.

Рисунок 43 – Робота з натуральними числами

 

Стан q₁ надає можливість зменшувати молодшу цифру на 1.

Якщо ця цифра є більшою за 1, то після її зменшення відразу буде виконано зупинення програми.

Якщо молодша цифра дорівнює 0, то замість неї буде записано цифру 9, виконано переміщення вліво і знову виконано дію віднімання. .

Якщо цифра, що зменшується на одиницю, сама дорівнює 1, то замість неї (тобто одиниці) буде записано цифру 0 і виконано перехід в стан q₂. .

Результат роботи програми наведено на рисунку 44.

Рисунок 44 – Результат зменшення натурального числа на одиницю

 

6.3 Увести натуральне число, яке закінчується на 10.

 

Якщо число закінчується на 10, то згідно з програмою:

– розглядаються всі цифри числа з переміщенням вправо до першої пустої клітинки, далі виконується переміщення вліво з переходом в стан q₁:

;

– розглядається остання цифра числа, яка в даному випадку дорівнює цифрі 0. Згідно з даною програмою замість цифри 0 записується цифра 9, виконується перехід вліво з подальшою обробкою наступної цифри і програма залишається в стані q₁:

;

– розглядається передостання цифра числа, яка в даному випадку дорівнює цифрі 1. Згідно з даною програмою замість цифри 1 записується цифра 0, виконується перехід вліво з подальшою обробкою наступної цифри (цифри 2) і програма переходить в стан q₂;

– перемістившись до цифри 2 в стані q₂, програма залишає в клітинці цифру 2 та виконує зупинення програми.

.

6.4 Увести натуральне число, яке закінчується двома нулями.

Проаналізувати результат та пояснити роботу програми в даному випадку.

6.5 Увести натуральне число, яке закінчується одиницею.

Проаналізувати результат.

Приклад 7

Розробити МТ, яка б виконувала копіювання заданого аргументу.

7.1 Обрати вхідний алфавіт А ={0, 1, ε}, де ε – пустий символ (пробіл).

7.2 Записати програму МТ для заданого вхідного ланцюжка на стрічці, який дорівнює двійковому числу 111. Представити МТ у вигляді таблиці відповідності, як це наведено на рисунку 45.

 

 

Рисунок 45 – Програма, призначена для копіювання аргументу

 

Зліва від кожної команди наведено представлення вхідного ланцюжка на стрічці до виконання даної команди. Символ, який знаходиться над головкою, позначено підкресленням [11].

 

1) q₀1 → q₁0R ε 1 11ε (в стані q₀ головка знаходиться під першою цифрою 1 та згідно з командою змінює стан на q₁, заміняє цифру 1 на цифру 0 та переміщується вправо);

2) q₁1 → q₁1R ε0 1 1ε (в стані q₁ не виконується заміна цифри 1 в другій клітинці, головка переміщується вправо);

3) q₁1 → q₁1R ε01 1 ε (в стані q₁ не виконується заміна цифри 1 в другій клітинці, головка переміщується вправо);

4) q₁ε → q₂*R ε011 ε (головка розміщується на символі ε, переходить в стан q₂, переміщується вправо, де додається символ «*». Головка залишилася на символі ε (див. п. 5));

5) q₂ε → q₃1L ε011* ε;

6) q₃* → q₃*L ε011 * 1ε;

7) q₃1 → q₃1L ε01 1 *1ε;

8) q₃1 → q₃1L ε0 1 1*1ε;

9) q₃0 → q₀0R ε 0 11*1ε;

10) q₀1 → q₁0R ε0 1 1*1ε;

11) q₁1 → q₁1R ε00 1 *1ε;

12) q₁* → q₂*R ε001 * 1ε;

13) q₂1 → q₂1R ε001* 1 ε;

14) q₂ε → q₃1L ε001*1 ε;

15) q₃1 → q₃1L ε001* 1 1ε;

16) q₃* → q₃*L ε001 * 11ε;

17) q₃1 → q₃1L ε00 1 *11ε;

18) q₃0 → q₀0R ε0 0 1*11ε;

19) q₀1 → q₁0R ε00 0 *11ε;

20) q₁* → q₂*R ε000 * 11ε;

21) q₂1 → q₂1R ε000* 1 1ε;

22) q₂1 → q₂1R ε000*1 1 ε;

23) q₂ε → q₃1L ε000*11 ε;

24) q₃1 → q₃1L ε000*1 1 1ε;

25) q₃1 → q₃1L ε000* 1 11ε;

26) q₃* → q₃*L ε000 * 111ε;

27) q₃0 → q₀0R ε00 0 *111ε;

28) q₀* → q₀*L ε000 * 111ε;

29) q₀0 → q₀1L ε00 0 *111ε;

30) q₀0 → q₀1L ε0 0 1*111ε;

31) q₀0 → q₀1L ε 0 11*111ε;

32) q₀ε → q_к1R ε 111*111ε.

Із прикладу видно, що МТ із стандартної початкової конфігурації, маючи на стрічці аргумент 111 та виконавши сукупність команд 1–32, перейшла в стандартний заключний стан, маючи на стрічці результат ε111*111ε.

Результат роботи програми в ALGO 2000 наведено на рисунку 46.

 

 

Рисунок 46 – Результат роботи програми, яка призначена для копіювання аргументу

 

7.3 Увести інше двійкове число в вигляді одиниць для копіювання. Проаналізувати отримані результати.

7.4 Доопрацювати наведену програму для введення нулів.

Приклад 8

Розробити МТ, яка визначає, чи ділиться на 5 без залишку десяткове число, розташоване на інформаційній стрічці. Якщо число ділиться без залишку на 5, то справа від числа потрібно написати слово «ДА», якшо не ділиться – слово «НЕТ». Головка знаходиться над лівою цифрою числа.

8.1 Обрати вхідний алфавіт: А ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, Д, А, Н, Е, Т}

8.2 Представити МТ у вигляді таблиці відповідності, як це наведено на рисунку 47.

 

Рисунок 47 – Функціональна схема для визначення кратності 5

 

У даній програмі:

– стан q₁ служить для пошуку правого кінця числа;

– стан q₂ служить для аналізу молодшої цифри числа. Якщо вона дорівнює цифрі 0 або цифрі 5, тобто число ділиться на 5, то виконується перехід в стан q₃, інакше – в стан q₅;

– стан q₃ служить для запису літери «Д» справа від числа на стрічці;

– стан q₄ служить для запису літери «А» справа від літери «Д» на стрічці та зупинення машини;

– стан q₅ служить для запису літери «Н» справа від числа на стрічці;

– стан q₆ служить для запису літери «Е» справа від літери «Н» на стрічці;

– стан q₇ служить для запису літери «Т» справа від літери «Е» на стрічці та зупинення машини.

8.3 Увести число, кратне 5, наприклад, 125. Результат роботи програми наведено на рисунку 48.

 

 

Рисунок 48 – Результат роботи програми

 

8.4 Увести число 1756. Відповідь МТ є слово «НІ».

8.5 Удосконалити МТ таким чином, шоб відповіді МТ писала українською мовою: «ТАК» або «НІ».

 

Приклад 9

Розробити МТ, яка б підраховувала кількість введених на інформаційну стрічку символів «*». Якщо ця кількість менша або дорівнює 9, то програма виводить цю кількість числом десяткової системи числення.

Головка може бути розташована або на першій або на останній клітинці стрічки.

9.1 Обрати вхідний алфавіт, який складається з цифр та символу: 0 1 2 3 4 5 6 7 8 9 *.

9.2 Представити МТ у вигляді таблиці відповідності (рис. 49).

 

Рисунок 49 – Таблиця відповідності для підрахунку кількості символів «*»

 

Результат роботи програми наведено на рисунку 50.

 

 

Рисунок 50 – Результат роботи програми

Програму для підрахунку кількості символів «*» можна спростити, що наведено на рисунку 51.

 

 

Рисунок 51 – Модіфікована програма підрахунку символів «*»

 

Результат роботи модифікованої програми наведено на рисунку 52.

 

 

Рисунок 52 – Результат роботи модіфікованої програми підрахунку символів «*»

9.3 Доопрацювати програму таким чином, щоб з її допомогою можна було обраховувати кількість введених символів «*», більших за число 9.

 

Приклад 10 Розробити МТ, яка виконує дію віднімання двох чисел, записаних у десятковій системі числення.Автомат у стані q₀ оглядає крайню праву цифру числа.

10.1 Обрати вхідний алфавіт, який складається з цифр та символу: 0 1 2 3 4 5 6 7 8 9 –.

10.2 Представити МТ у вигляді таблиці відповідності (рис. 53).

 

Рисунок 53 – Функціональна схема віднімання двох чисел

 

У даній програмі:

– стан q₀ служить для віднімання одиниці;

– стан q₁ служить для здійснення переходу до першого числа;

– стан q₂ служить для віднімання одиниці від першого числа;

– стан q₃ служить для зсуву каретки вправо до пробіла;

– стан q₄ служить для знищення зайвих символів.

Переміщення каретки до знака «–» означає, що в стані q₀ друге число вичерпане.

Результат роботи програми наведено на рисунку 54.

 

 

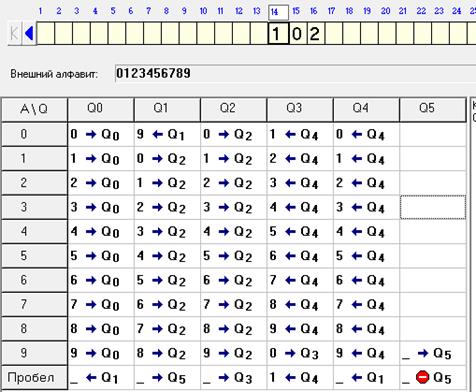
Рисунок 54 – Результат віднімання двох чисел

 

Приклад 11

Скласти функціональну схему МТ, яка могла б число, подане в десятковій системі числення, записувати в зворотньому порядку.

Каретка може знаходиться як на крайній правій цифрі числа, так і на крайній лівій цифрі числа.

11.1 Обрати вхідний алфавіт, який складається з цифр: 0 1 2 3 4 5 6 7 8 9.

11.2 Представити МТ у вигляді таблиці відповідності (рис. 55).

 

 

Рисунок 55 – Функціональна схема МТ

 

11.3 Увести число 102 та запустити програму для виконання.

Результат роботи МТ наведено на рисунку 56.

 

 

Рисунок 56 – Результат роботи МТ для запису числа

в зворотньому порядку

Контрольні питання

 

1 Яким чином зміниться роботи програми (рис. 38), якщо головка буде знаходитися не на першій цифрі числа, а на останній?

2 Яку відповідь буде отримано після вводу числа 12370, якщо використати програму, наведену на рисунку 38?

3 Яку відповідь буде отримано після вводу числа 12477, якщо використати програму, наведену на рисунку 38?

4 Який результат буде отримано за використання програми, зображеної на рисунку 45, якщо замість одиниць ввести нулі?

5 Які дії будуть виконуватися, якщо в програмі, наведеній на рисунку 53, використовувати тільки перші два стовпчика програми?

 

ЛАБОРАТОРНА РОБОТА 3