Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм сортировки «пузырек»
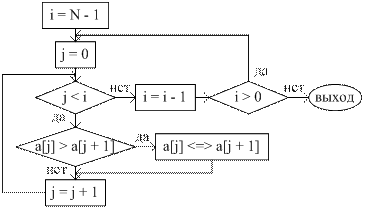
1. Полагаем i = N – 1. 2. Обнуляем индекс j. 3. Если a [ j ] > a [ j + 1], то меняем местами a [ j ] и a [ j + 1]. 4. Увеличиваем j на единицу. 5. Если j < i идем на шаг 3. 6. Уменьшаем i на единицу. 7. Если i > 0, идем на шаг 2. Приведем пример. Часть массива, в которой на очередном шаге выталкивается максимальный элемент, выделена синим цветом, сравниваемые элементы – красным.
Очевидно, что “пузырек” – устойчивая сортировка. Теперь приведем блок-схему сортировки “пузырек”.
Улучшения этого алгоритма довольно очевидны. Как видно из примера, на последних итерациях элементы сравниваются «впустую», так как перестановок на предыдущих итерациях не было, а значит, массив был уже упорядочен. Поэтому следует запоминать, была ли хотя бы одна перестановка.
Однако запоминать можно не только сам факт обмена (обмен произошел), но и место (индекс R) последнего обмена. Понятно, что правее этого места массив упорядочен, поэтому следующий просмотр массива можно заканчивать на этом месте, а не идти до заранее заданного i (заметим, что R ≤ i). Приведем пример. Часть массива, в которой на очередном шаге выталкивается максимальный элемент, выделена синим цветом, сравниваемые элементы – красным, R – индекс последнего обмена (место последнего обмена обведено в рамку, сначала R =0).
Теперь приведем блок-схему улучшенной сортировки “пузырек”. Здесь R – место последнего обмена, Rt – индекс текущего обмена; если индексы становятся равны, это означает, что обмена не было.
Но возникает вполне логичный вопрос: почему мы все время двигаемся слева направо, выгоняя самый “тяжелый” элемент? Разве нельзя в свое время двигаться справа налево, выталкивая самый “легкий” элемент? Получающаяся при этом сортировка называется “ шейкерной ”. Рассмотрим массив из предыдущего примера, и отсортируем его “шейкерной” сортировкой. Часть массива, в которой на очередном шаге выталкивается максимальный или минимальный элемент, выделена синим цветом, сравниваемые элементы – красным, R – индекс последнего обмена при движении слева направо, L – при движении справа налево.
Теперь приведем блок-схему сортировки “шейкер”. Здесь L – левая граница интервала, R – правая граница интервала, Rt – индекс текущего обмена при движении слева направо, Lt – индекс текущего обмена придвижении справа налево; если индексы становятся равны (т.е. R = Rt, L = Lt), это означает, что обмена не было.
В худшем для сортировки «пузырек» случае максимальный элемент находится в начале массива, поэтому на первой итерации нам понадобится (N –1) сравнение и столько же обменов. После первой итерации граница R сдвинется влево на единицу, то есть в худшем случае понадобится (N –2) сравнения и столько же обменов, и т. д. На последней итерации понадобится одно сравнение и один обмен, так что общее число сравнений и обменов есть
Сортировка Шелла
В 1959 году Шеллом было предложено усовершенствование сортировки с помощью прямой вставки. Модификация классического метода основана на следующей идее. Сначала происходит сортировка массивов небольшой длины (подмассивов исходного массива), а потом сортируются массивы большой длины, но, благодаря предыдущим сортировкам, частично упорядоченные, что позволяет ограничить число сравнений. Шелл предложил сортировать массив методом прямой вставки, но расстояние между элементами сделать равным не 1, а некоторому шагу k 1. Например, N = 10, k 1 = 3. Подмассивы выделены разными цветами.
После этого получаем k 1 упорядоченный подмассив. Далее уменьшаем шаг и повторяем ту же процедуру сортировки, т.е. практически заменяем сортировку массива длины N сортировкой некоторого числа массивов меньшей длины. Последняя сортировка идет с шагом 1, то есть это обычная прямая вставка. Рассмотрим алгоритм подробнее на примере. Задаем множество шагов { k 1, k 2, …, km }, причем
Полагаем k 1 = 3, подмассивы выделены разными цветами.
Каждый из подмассивов сортируем методом прямой вставки.
Полагаем k 2 = 2, подмассивы выделены разным цветом.
Каждый из подмассивов сортируем методом прямой вставки.
Полагаем k 3 = 1 и сортируем массив обычной прямой вставкой.
Алгоритм сортировки Шелла
1. Формируем массив шагов k 0 = 1 < k 1 <…< km -1.
2. Полагаем p = m – 1. 3. Если p ≥ 0, выполняем шаги 4 – 7. 4. Полагаем q = 0. 5. Если q < kp, выполняем шаги 5.1 – 5.6, т. е., сортируем массив a [ q ], a [ q + kp ], a [ q +2 kp ],… методом прямой вставки. Иначе идем на шаг 7. 5.1. Полагаем j = q + kp 5.2. Пока j < N, выполняем шаги 5.3 – 5.6. 5.3. Полагаем i = j – kp, x = aj. 5.4. Пока i ≥ 0 и a [ i ] > x, полагаем a [ i + kp ] = a [ i ], уменьшаем i на kp. 5.5.Полагаем a [ i + kp ] = x . 5.6. Увеличиваем j на kp. 6. Увеличиваем q на 1. 7. Уменьшаем p на 1 и идем на шаг 3.
Блок-схема сортировки Шелла
На первый взгляд можно усомниться: если необходимо несколько процессов сортировки, причем в каждый включаются все элементы, то не добавят ли они больше работы, чем сэкономят? Однако на каждом этапе либо сортируется относительно мало элементов, либо элементы уже довольно хорошо упорядочены и требуется сравнительно немного перестановок. Обратим внимание на предыдущий пример. Когда производилась сортировка массива с шагом k = 1, элементы либо оставались на месте (10, 11, 18, 40), либо сдвигались на одну позицию назад (14, 21, 27). Так произошло потому, что перед этим были отсортированы части массива при k = 2, то есть для массива к моменту его сортировки шагом k = 1 верно следующее неравенство: a [ i ] ≥ a [ i– 2]. Поэтому для каждого элемента a [ i ] массива при сортировке с шагом k = 1 требуется не более двух сравнений (а не i, как в обычном методе прямой вставки!). Если же перед сортировкой с шагом k была проведена сортировка с шагом l > k, то для массива верно a [ i ] ≥ a [ i–l ], a [ i ] ≥ a [ i- 2 l ], … и т.д., т. е., в частности, a [ i ] ≥ a [ i–p ], где p – наименьшее общее кратное чисел k и l. Следовательно, для элемента a [ i ] потребуется не более чем Ясно, что такой метод в результате дает упорядоченный массив, т.к. последняя сортировка выполняется с шагом k = 1. и каждый проход от предыдущих только выигрывает, т.к. получает уже частично упорядоченные подмножества элементов. Также очевидно, что расстояния в группах (шаги) можно уменьшать по-разному, лишь бы последнее было единичным. Сортировка Шелла не является устойчивой. Анализ этого алгоритма поставил несколько математических проблем, многие из которых так еще и не решены. В частности, не известно, какие расстояния дают наилучшие результаты. Но удивительным фактом является то, что они не должны быть множителями друг друга. Справедлива такая теорема: если k -отсортированную последовательность i -отсортировать, то она остается k -отсортированной. Кнут показал, что имеет смысл использовать такую последовательность (записана в обратном порядке): 1, 4, 13, 40, 121, …, где hk -1 = 3 hk + 1, ht = 1 и t = [log3 N ] – 1. Он рекомендует и другую последовательность шагов: 1, 3, 7, 15, 31, …, где hk -1 = 2 hk + 1, ht = 1 и t = [log2 N ]–1. В последнем случае для сортировки методом Шелла затраты пропорциональны N 1.2. Пирамидальная сортировка
Пирамидальная сортировка является улучшением сортировки с помощью прямого выбора. Но, в отличие от прямого выбора, мы запоминаем не только место наибольшего элемента массива, но и локальные максимумы тоже.
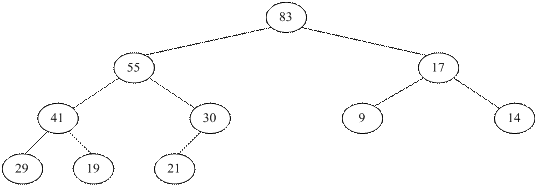
Введем сначала несколько определений. Определение. Подчиненными элементами для элемента a [ i ] называются элементы a [2 i +1], a [2 i +2]. Говорят, что a [ i ] не имеет подчиненных, если Например, для элемента a [0] подчиненными являются a [1] и a [2], для a [1] – элементы a [3] и a [4]. Схему «подчиненности» элементов можно изобразить в виде дерева. Причем, если перечислять вершины дерева по ярусам сверху вниз, а в каждом ярусе слева направо (на рисунке показано стрелочками), то мы получим массив a [0], a [1], …, a [ N –1] в его естественном порядке.
Определение. Массив называется пирамидой, если каждый элемент массива не меньше подчиненных ему элементов, то есть a [ i ] ≥ a [2 i +1] и a [ i ] ≥ a [2 i +2] (если хоть один подчиненный элемент существует). Например, массив {83, 55,17, 41, 30, 0, 14, 28, 19, 21} является пирамидой.
Как легко заметить, на «вершине» пирамиды находится максимальный элемент массива, т. е. a [0] ≥ a [ i ] для любого Превращаем произвольный массив в пирамиду. Считаем массив a [0], a [1], …, a [ k ] неупорядоченным, k = N – 1. Меняем элемент a [0] с последним элементом a [ k ] неупорядоченной части. Перестраиваем неупорядоченную часть a [0], a [1], …, a [ k –1] так, чтобы она стала пирамидой. Процедура превращения массива в пирамиду практически сводится к нахождению места в массиве для его элементов, имеющих подчиненные. Для того, чтобы найти место для элемента массива очень удобно использовать процедуру, называемую «протаскиванием элемента через пирамиду». Рассмотрим ее подробней. Выделим в массиве элемент a [ i ]. Пусть поддеревья, корнями которых являются подчиненные a [ i ] элементы a [2 i +1] и a [2 i +2], являются пирамидами. Тогда превращение дерева с корнем a [ i ] в пирамиду сводится к тому, чтобы найти место для a [ i ], не перестраивая дерево, а лишь сдвигая элементы по одной из ветвей. Если a [ i ] ≥ a [2 i +1] и a [ i ] ≥ a [2 i +2], то массив уже является пирамидой, в противном случае, поменяем a [ i ] с максимальным из подчиненных ему элементов. Очевидно, что после такого обмена a [ i ] ≥ a [2 i +1] и a [ i ] ≥ a [2 i +2]. Будем повторять этот шаг, пока a [ i ] либо не достигнет нижнего яруса, либо не станет больше подчиненных ему элементов. Рассмотрим процедуру «протаскивания» на примере. Пусть мы имеем массив: {17, 42, 22, 33, 37, 19, 13, 20, 11, 21}.
Этот массив почти является пирамидой. Необходимо только «протащить» первый элемент, то есть найти ему место в пирамиде. «Протаскиваемый» элемент выделен красным цветом, элементы с которыми на данном этапе происходит сравнение – синим. Траектория «протаскивания» выделена зеленым.
Очевидно, что число сравнений пропорционально высоте дерева.
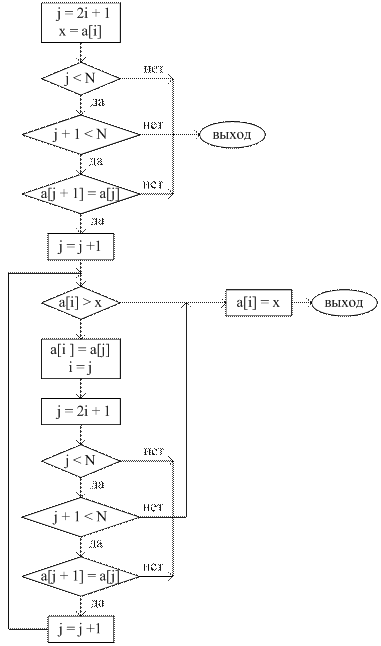
Алгоритм «протаскивания» a [ i ] через пирамиду 1. Полагаем j = 2 i + 1, x = a [ i ]. 2. Если j < N, алгоритм завершен. 3. Если a [ j +1] > a [ j ] и j + 1 < N, то полагаем j = j + 1. 4. Пока a [ j ] > x делаем: 4.1. полагаем a [ i ] = a [ j ], i = j; 4.2. полагаем j = 2 i + 1; 4.3. если j ³ N идем на шаг 5; 4.4. если j + 1 < N и aj + 1 > aj, то полагаем j = j + 1; 5. Полагаем a [ i ] = x и идем на шаг 2.
Блок-схема процедуры «протаскивания» a [ i ] через пирамиду
Сама сортировка состоит из двух этапов, каждый из которых включает в себя процедуру «протаскивания»: 1. построение пирамиды, т.е. превращение произвольного массива в пирамиду; 2. собственно сортировка.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.32.116 (0.083 с.) |


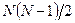 . Таким образом, трудоемкость имеет порядок
. Таким образом, трудоемкость имеет порядок  . Те же рассуждения верны и для шейкерной сортировки.
. Те же рассуждения верны и для шейкерной сортировки.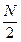 ≥ k 1 > k 2 >…> km = 1. Например, N = 10, k 1 = 3, k 2 = 2, k 3 = 1.
≥ k 1 > k 2 >…> km = 1. Например, N = 10, k 1 = 3, k 2 = 2, k 3 = 1.
 сравнений.
сравнений. .
.
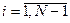 . Отсюда вытекает идея пирамидальной сортировки.
. Отсюда вытекает идея пирамидальной сортировки.