
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Статично невизначені стрижневі конструкції
Існує багато стрижневих конструкцій, в яких стрижні шарнірно з'єднані один з одним, однак зусилля в стрижнях не можна однозначно визначити з рівнянь рівноваги її вузлів, тому що число невідомих зусиль виявляється більше числа рівнянь рівноваги вузлів конструкції. Подібні конструкції називають статично невизначеними. Різниця між числом шуканих зусиль і числом незалежних рівнянь статики для їхнього визначення називають степенем статичної невизначеності конструкції. Наприклад, плоска конструкція із трьох невагомих стрижнів, шарнірно прикріплених верхніми кінцями до стелі й шарнірно з'єднаних між собою нижніми кінцями, є один раз статично невизначеною конструкцією.
Для визначення трьох зусиль у стрижнях можна скласти для їхнього визначення лише два незалежні рівняння рівноваги нижнього вузла: Для однозначного визначення невідомих зусиль у стрижнях статично невизначеної конструкції потрібно доповнити рівняння статики іншими рівняннями, які найбільше часто виводять із припущення про пружну деформацію стрижнів. Очевидно, після пружної деформації стрижнів конструкції (якщо її розібрати) деформовані стрижні можна знову з'єднати колишніми шарнірними в'язями. На цій підставі додаткові рівняння для визначення зусиль стрижнях називають рівняннями сумісності деформацій. Покажемо на прикладі, як встановити рівняння сумісності деформацій. Приклад 1. Крайні стрижні конструкції, зображеної на рисунку, однакові і є сталевими, середній стрижень – мідний, довжина крайніх стрижнів
Розв'язання. Складемо рівняння рівноваги осі шарніра А. На вузол А діють сили
Розглядувана конструкція один раз статично невизначена, оскільки число невідомих зусиль дорівнює трьом, а рівнянь рівноваги – два. Складемо додаткове рівняння (рівняння сумісності деформацій). Під дією сили Q усі стрижні конструкції отримають пружні подовження. Оскільки стрижні 1 і 2 однакові і
де Мислено розберемо конструкцію і надамо стрижням зазначені подовження, тоді, обертаючи стрижні 1 і 2 навколо точок B і D, зможемо поєднати кінці всіх стрижнів конструкції в новій точці A3. Дуги A1A3 і A2A3, які описують кінці подовжених стрижнів 1 і 2, замінюємо через їхню малість прямолінійними відрізками A1A3 і A2A3, перпендикулярними відповідно стрижням AB і AD.
У прямокутному трикутнику AA1A3,
Це і є рівняння сумісності деформацій стрижнів даної конструкції. Замінимо в рівнянні сумісності деформацій
Розв'яжемо систему трьох рівнянь (7.1), (7.2). Маємо
Підставимо отримані вирази для
З цього рівняння знаходимо
За відомим зусиллям
Для визначення шуканих площ
З цих нерівностей визначимо найменші значення площ
Приклад 2. Три стрижні кронштейна виконані з одного матеріалу. Площа поперечного перерізу першого стрижня
Розв'язання. Складемо рівняння рівноваги вузла
Ця система сил є плоскою, тому рівняння рівноваги системи сил такі:
Як бачимо, розглядувана стрижнева конструкція один раз статично невизначена. Доповнимо рівняння рівноваги вузла
Мислено розберемо вузол
Виключивши з отриманих виразів для
Замінимо в цьому рівнянні подовження
одержимо рівняння
що доповнює рівняння статики до визначеної системи лінійних алгебраїчних рівнянь відносно шуканих зусиль Спростимо одержане рівняння, прийнявши до уваги, що за умовою задачі
Таким чином, система рівнянь для визначення зусиль у стрижнях кронштейна виявляється такою
Розв'язавши систему, одержимо
Від'ємний знак значень модулів сил, що деформують другий і третій стрижні кронштейна, означає, що їх напрям протилежний прийнятому визначально напряму, тобто сили Визначимо відповідні знайденим зусиллям напруження в стрижнях:
Знак мінус у значеннях напружень
|
||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.108 (0.023 с.) |

 .
. , а середнього –
, а середнього –  . Допустиме напруження для сталі
. Допустиме напруження для сталі  , а для міді
, а для міді  . Потрібно встановити міцні розміри поперечних перерізів цих стрижнів, якщо на конструкцію діє сила Q.
. Потрібно встановити міцні розміри поперечних перерізів цих стрижнів, якщо на конструкцію діє сила Q.
 ,
, 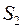 ,
,  з боку стрижнів і зовнішня сила Q. Ця система сил збіжна, тому рівняння рівноваги вузла мають вигляд:
з боку стрижнів і зовнішня сила Q. Ця система сил збіжна, тому рівняння рівноваги вузла мають вигляд:

 ,
,
 (7.1)
(7.1)
 , що випливає з першого рівняння рівноваги, то зрозуміло, що подовження
, що випливає з першого рівняння рівноваги, то зрозуміло, що подовження  і
і  цих стрижнів однакові:
цих стрижнів однакові:  . За законом Гука
. За законом Гука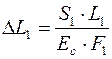 ,
,  ,
, – модуль Юнга сталевого стрижня,
– модуль Юнга сталевого стрижня,  – модуль Юнга мідного стрижня,
– модуль Юнга мідного стрижня,  і
і  – площі поперечного перерізу першого і третього стрижнів.
– площі поперечного перерізу першого і третього стрижнів.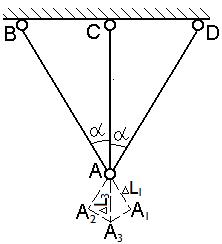
 ,
,  ,
,  , тому
, тому .
. . (7.2)
. (7.2) (7.3)
(7.3)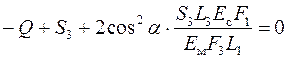 .
.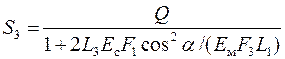 .
. .
. і
і  ,
,  .
.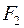 ,
,  ,
,  .
. , другого –
, другого –  , третього –
, третього –  . Вага вантажу Р =5000 кГ. Визначити напруження в поперечних перерізах стрижнів.
. Вага вантажу Р =5000 кГ. Визначити напруження в поперечних перерізах стрижнів.
 . Для цього зобразимо сили, що діють на вузол зі сторони стрижнів та силу Р:
. Для цього зобразимо сили, що діють на вузол зі сторони стрижнів та силу Р:

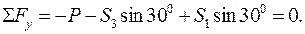
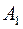 на площині осей xy і що стрижні 1, 2, 3 одержали при цьому подовження
на площині осей xy і що стрижні 1, 2, 3 одержали при цьому подовження  Нехай
Нехай  – одиничні вектори на стрижнях 1, 2, 3 (див. наведений нижче рисунок). Як видно з рисунка, ці вектори характеризуються координатами:
– одиничні вектори на стрижнях 1, 2, 3 (див. наведений нижче рисунок). Як видно з рисунка, ці вектори характеризуються координатами: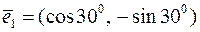 ,
,  ,
, 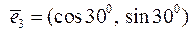 .
.
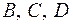 зі стіною. Розглянемо вектор
зі стіною. Розглянемо вектор 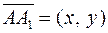 . Очевидно,
. Очевидно, ,
,  ,
, .
. величини
величини 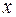 та
та 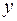 , прийдемо до шуканого рівняння сумісності деформацій стрижнів кронштейна
, прийдемо до шуканого рівняння сумісності деформацій стрижнів кронштейна .
. згідно із законом Гука
згідно із законом Гука ,
,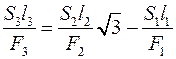 ,
, , а
, а  . Будемо мати
. Будемо мати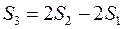 .
.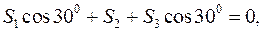
 ,
, .
.
 й
й 

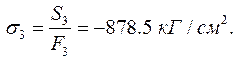
 і
і  вказує на те, що ці напруження є стискаючими.
вказує на те, що ці напруження є стискаючими.


