
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Статично визначені стрижневі конструкції
Стрижневі конструкції із прямолінійних стрижнів широко використовуються в будівництві й машинобудуванні. Обмежимося розглядом найпоширенішого типу стрижневих конструкцій – фермами. Фермою називається конструкція із прямолінійних стрижнів, які шарнірно з'єднані один з одним так, щоб конструкція була геометрично незмінною. Будемо розглядати прості плоскі ферми. Проста плоска ферма створюється в такий спосіб: до основного трикутника, утвореного трьома шарнірно з'єднаними стрижнями, приєднують два інших стрижня для утворення нового трикутника. До отриманого трикутника додають два нові стрижня і т.д.
Установимо співвідношення між числом стрижнів у простій фермі й числом вузлів (шарнірів), при якім ферма буде геометрично незмінною. Нехай ферма складається із При розрахунках ферми на міцність спочатку визначають реакції опор потім зусилля в її стрижнях. При цьому виходять із того, що стрижні є твердими тілами й що силами ваги стрижнів можна знехтувати (через їхню малість у порівнянні з іншими силами навантаження ферми). Вважається, що стрижні з'єднані ідеальними шарнірами, які розміщені тільки на кінцях стрижнів і що зовнішні сили прикладені тільки до вузлів ферми, тобто до шарнірів. Ці вихідні припущення суттєво полегшують визначення зусиль у стрижнях ферми й несуттєво позначаються на точності їх визначення. Оскільки кожний стрижень ферми вважається невагомим, а діючі на стрижень сили прикладені до його кінців, то будь-який стрижень ферми або перебуває у розтягнутому або стиснутому стані. Сили стиснення або розтягування будь якого стрижня прикладені до кінців цього невагомого стрижня, тому згідно з аксіомою 1 вони спрямовані уздовж стрижня ферми. Якщо зусилля в усіх стрижнях ферми можна визначити з рівнянь рівноваги вузлів, то таку ферму називають статично визначеною, а якщо ні, то статично невизначеною. Проста плоска ферма відноситься до статично визначених ферм. Зусилля в стрижнях такої ферми визначають або методом вирізання вузлів, або методом перерізів. Метод вирізання вузлів вважається основним, метод перерізів використовують звичайно для контролю правильності результатів розрахунків зусиль у стрижнях ферми за методом вирізання вузлів.
Метод вирізання вузлів полягає в наступному: 1. Потрібно перенумерувати стрижні плоскої ферми. Звільнити ферму від в'язів (опор), їхню дію на ферму замінити реакціями. Визначити величини реакцій з рівнянь рівноваги ферми як твердого тіла, на яке діє плоска система сил (три рівняння рівноваги (4.3)). 2. Знайти вузол (шарнір) ферми, в якім збігаються тільки два стрижні. Зобразити зовнішні сили, що діють на цей вузол, а також і сили з боку відрізаних стрижнів (вони спрямовані уздовж вилучених стрижнів, тому що вагою стрижнів ферми нехтують). Вони являють собою шукані зусилля в стрижнях, відрізаних мислено від вузла. 3. Розумно вибрати осі декартової системи координат з початком у вузлі ферми. Скласти рівняння рівноваги вузла, враховуючи, що до нього прикладена збіжна система сил. 4. Визначити з рівнянь рівноваги вузла ( 5. Перейти до наступного вузла, в якім збігаються не більш двох стрижнів з невідомими зусиллями. Метод перерізів: 1. Визначити реакції опор ферми з рівнянь рівноваги
Зрозуміло, осі декартової системи координат 2. Мислено розсікти ферму на дві частини так, щоб перетин проходив не більш, ніж через три стрижні. 3. Вибрати ту частину ферми, до якої прикладено менше зовнішніх сил. Іншу частину відкинути, замінивши її дію на ту частину, що залишилася, силами, спрямованими уздовж відрізаних стрижнів.
4. Визначити ці сили (зусилля в стрижнях) з рівнянь рівноваги обраної частини ферми, з'ясувати чи є вони стискаючими або розтягувальними. 5. Звірити значення отриманих зусиль із відповідними значеннями зусиль у таблиці, складеної за допомогою методу вирізання вузлів.
Приклад 1. Визначити зусилля в стрижнях мостової ферми.
Розв’язання. Перенумеруємо стрижні ферми як вказано на рисунку. Замінимо дію опор на ферму реакціями
З цих рівнянь визначимо величини реакцій опор ферми Виріжемо вузол А, в якому збігаються два стрижня ферми. Дія відкинутих стрижнів на вузол замінюємо силами, спрямованими вздовж стрижнів. На наступному рисунку зображені сили, що діють на вузол А.
Складемо рівняння рівноваги вузла А
З цих рівнянь визначимо шукані зусилля
Побачимо тоді, що стрижень 1 стиснутий, а стрижень 6 – розтягнутий. Занесемо зусилля в цих стрижнях (з відповідними знаками) у таблицю зусиль в стрижнях ферми (стор. 40). Виріжемо тепер вузол С, оскільки в цьому вузлі збігаються два стрижні з невідомими зусиллями. Зобразимо сили, прикладені до вузла, враховуючи при цьому, що стрижень 1 стиснутий силою
Складемо рівняння рівноваги вузла С
З цих рівнянь визначимо
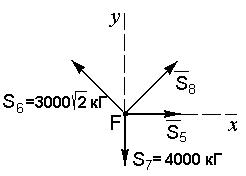
Виріжемо вузол F. Зобразимо прикладені до нього сили.
Складемо рівняння рівноваги вузла F
Визначаємо з цих рівнянь
Виріжемо вузол D.
Складемо рівняння рівноваги вузла D (сили, прикладені до цього вузла, зображені на рисунку)
З рівнянь рівноваги знаходимо
Виріжемо вузол B. Зобразимо сили, прикладені до вузла B.
Складемо таке рівняння рівноваги вузла
Звідси
Тепер занесемо у таблицю результатів усі визначені зусилля в стрижнях ферми
Нагадаємо, що в таблиці, знаком «–» помічені зусилля в стиснутих стрижнях ферми. Приклад 2. Визначити зусилля в стрижнях ферми з номерами 2, 5, 6, 7, 8 методом перерізів.
Розв’язання. Скористаємося тим, що реакції опор ферми визначені при розв’язанні попередньої задачі. Проведемо переріз I через три стрижня з номерами 5, 8, і 2. Замінимо дію відкинутих частин стрижнів на праву половину ферми силами
Складемо рівняння рівноваги цієї частини
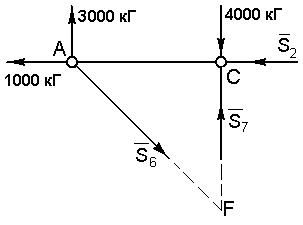
Проведемо переріз II ферми через стрижні 2, 7 і 6 і розглянемо ліву частину ферми
Скористаємося таким варіантом рівнянь рівноваги для цієї частини
Таким чином,
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.16.254 (0.046 с.) |

 стрижнів і
стрижнів і  вузлів. На утворення основного трикутника потрібно три стрижні й три вузли. На утворення кожного наступного трикутника потрібно два стрижні й один вузол. Тому для
вузлів. На утворення основного трикутника потрібно три стрижні й три вузли. На утворення кожного наступного трикутника потрібно два стрижні й один вузол. Тому для  вузлів, які пішли на утвір допоміжних трикутників, буде потрібно
вузлів, які пішли на утвір допоміжних трикутників, буде потрібно 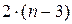 стрижнів. Таким чином,
стрижнів. Таким чином, 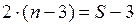 . Звідси одержуємо шукане співвідношення між числом
. Звідси одержуємо шукане співвідношення між числом 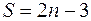 .
.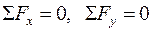 ) невідомі зусилля у двох стрижнях ферми, з'ясувати чи є вони стискаючими або розтягувальними. Вписати їхні значення в заздалегідь складену таблицю (у першому рядку таблиці перелічуються номери стрижнів, у другому рядку відповідні значення зусиль в стрижнях). Якщо зусилля в стрижні є стискаючим, то його значення записується в таблицю зі знаком мінус.
) невідомі зусилля у двох стрижнях ферми, з'ясувати чи є вони стискаючими або розтягувальними. Вписати їхні значення в заздалегідь складену таблицю (у першому рядку таблиці перелічуються номери стрижнів, у другому рядку відповідні значення зусиль в стрижнях). Якщо зусилля в стрижні є стискаючим, то його значення записується в таблицю зі знаком мінус.
 потрібно вибрати так, щоб рівняння рівноваги ферми можна було найбільш просто скласти.
потрібно вибрати так, щоб рівняння рівноваги ферми можна було найбільш просто скласти.

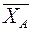 ,
, 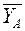 ,
, 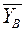 . Складемо рівняння рівноваги ферми
. Складемо рівняння рівноваги ферми ,
,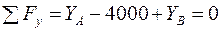 ,
, .
. ,
,  ,
,  .
.
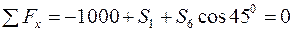 ,
, ,
, ,
, 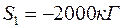 . Зауважимо, що від’ємне значення величини сили
. Зауважимо, що від’ємне значення величини сили  означає, що в дійсності напрям вектора
означає, що в дійсності напрям вектора  протилежний напряму, вказаному на рисунку. Зобразимо вірні напрями сил
протилежний напряму, вказаному на рисунку. Зобразимо вірні напрями сил  , що діють на вузол А ферми
, що діють на вузол А ферми
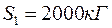 .
.
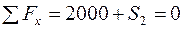 ,
, .
. ,
,  . Вірні напрями зусиль
. Вірні напрями зусиль 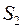 і
і  вказані на рисунку.
вказані на рисунку.
 ,
,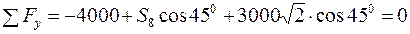 .
. ,
,  .
.
 ,
,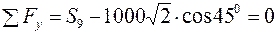 .
.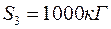 ,
,  .
.
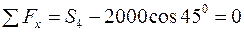 ,
,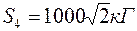 .
.

 та
та 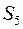 .
.
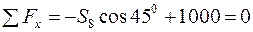
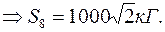
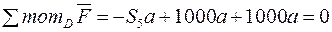

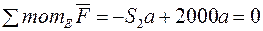
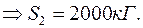



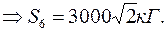

 ,
, 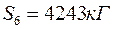 ,
, 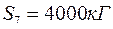 ,
, 


