
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Спрощення довільної системи сил
Введемо два нові важливі поняття статики: момент сили відносно точки й момент сили відносно осі. Нехай до точки
Якщо точка Нехай до точки
Система сил Нехай на тверде тіло діє довільна скінчена система сил
Після переносу точок прикладання всіх сил у точку Відомо, що дія декількох пар на тіло еквівалентна дії на тіло однієї пари сил, момент якої дорівнює сумі моментів усіх пар. Тому стає очевидним, що довільна система діючих на тіло сил
Вектор
Отже, доведена основна теорема статики: довільна система сил Одержимо тепер умови рівноваги тіла під дією довільної скінченої системи сил
На практиці користуються скалярними умовами рівноваги тіла. У деякій точці
Якщо система сил
Інші рівняння (4.2) перетворюються в тотожності. Приклад. Однорідна полиця ABCD вагою G, приєднана до вертикальної стінки за допомогою шарнірів A і B, утримується в горизонтальному положенні мотузкою ЕН. Визначити натяг T мотузки і реакції
Розв'язання. Звільнимо полку від в'язів (мотузки, шарнірів А і В), а їх дію на полку замінимо реакціями
З передостаннього рівняння рівноваги знайдемо
З останнього визначимо
З четвертого рівняння знайдемо
Нескладно переконатися, використовуючи перше і третє рівняння рівноваги, що
Таким чином, у розглянутій задачі
Приклад 2. Однорідний гладкий стрижень КС вагою
Розв'язання. На стрижень діє плоска система сил
З рисунку видно, що Підставивши знайдені значення АС і h в рівняння рівноваги, отримаємо
Звідси
Отже,
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.36.192 (0.053 с.) |
 твердого тіла прикладена сила
твердого тіла прикладена сила  . Моментом сили
. Моментом сили  тіла називають вектор
тіла називають вектор  , який позначають символом
, який позначають символом  .
.
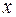 декартової системи координат, то проекцію вектора
декартової системи координат, то проекцію вектора  . З курсу аналітичної геометрії відомо, що координати вектора в декартовій системі координат
. З курсу аналітичної геометрії відомо, що координати вектора в декартовій системі координат  дорівнюють проекціям цього вектора на осі
дорівнюють проекціям цього вектора на осі  . Отже, якщо точка
. Отже, якщо точка  ,
,  ), де
), де  тіла дві протилежно спрямовані сили
тіла дві протилежно спрямовані сили 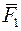 й
й  , паралельні силі
, паралельні силі  й рівні їй за величиною.
й рівні їй за величиною.
 і
і  еквівалентна силі
еквівалентна силі  . Таким чином, сила
. Таким чином, сила  . Це твердження називають лемою про паралельний перенос сили.
. Це твердження називають лемою про паралельний перенос сили. . Виберемо в тілі довільну точку
. Виберемо в тілі довільну точку 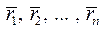 відкладені із точки
відкладені із точки 
 пар з моментами
пар з моментами  , …,
, …,  .
. .
. називають головним моментом вихідної системи сил відносно центру приведення
називають головним моментом вихідної системи сил відносно центру приведення  .
. та
та  , то це буде означати, що тіло перебуває у рівновазі, тобто система сил
, то це буде означати, що тіло перебуває у рівновазі, тобто система сил  , то ясно, що й для будь-якої іншої точки
, то ясно, що й для будь-якої іншої точки  тіла
тіла  й
й  (4.1)
(4.1) й прирівнюють відповідні координати векторів у правих і лівих частинах векторних рівностей (4.1). Отже, скалярні умови рівноваги тіла під дією системи сил
й прирівнюють відповідні координати векторів у правих і лівих частинах векторних рівностей (4.1). Отже, скалярні умови рівноваги тіла під дією системи сил 
 (4.2)
(4.2) (4.3)
(4.3) і
і  шарнірів, якщо
шарнірів, якщо 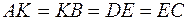 ,
,  . Мотузка EH утворює з полицею кут
. Мотузка EH утворює з полицею кут  .
.
 . Реакції
. Реакції 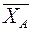 і
і  , а реакцію
, а реакцію  і
і  . Сила
. Сила  прикладена в центрі полки. Всі перераховані сили зображені на рисунку. Система сил (
прикладена в центрі полки. Всі перераховані сили зображені на рисунку. Система сил ( ,
,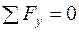 ,
, ,
, ,
, ,
, .
.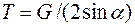 .
.
 .
.
 .
. ,
,  . Оскільки
. Оскільки  і
і  , то з урахуванням перпендикулярності складових
, то з урахуванням перпендикулярності складових  і
і  отримуємо
отримуємо ,
,  .
. .
. і довжиною 4м знаходиться в рівновазі в вертикальній площині. Верхньою частиною стрижень спирається на вертикальну стінку АВ довжиною 3м. Нижньою частиною стрижень спирається на гладку горизонтальну площину. Кінець С стрижня прив'язаний тросом АС до стіни. Визначити силу натягу Т троса і реакції
і довжиною 4м знаходиться в рівновазі в вертикальній площині. Верхньою частиною стрижень спирається на вертикальну стінку АВ довжиною 3м. Нижньою частиною стрижень спирається на гладку горизонтальну площину. Кінець С стрижня прив'язаний тросом АС до стіни. Визначити силу натягу Т троса і реакції  і
і  стіни і горизонтальній площині.
стіни і горизонтальній площині.
 ,
,  під дією яких він знаходиться в рівновазі. Рівнодіюча
під дією яких він знаходиться в рівновазі. Рівнодіюча 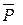 сил тяжіння всіх матеріальних частинок стрижня, прикладена в центрі ваги О стрижня (
сил тяжіння всіх матеріальних частинок стрижня, прикладена в центрі ваги О стрижня ( за способом симетрії). Складемо рівняння рівноваги стрижня, керуючись формулами (4.3)
за способом симетрії). Складемо рівняння рівноваги стрижня, керуючись формулами (4.3) ,
,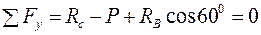 ,
, .
. ,
,  .
. ,
,  ,
, .
. ,
, 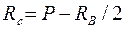 ,
, .
. ,
,  ,
, 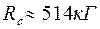 .
.


