
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Спрощення системи паралельних сил
Нехай на тверде тіло діє система паралельних сил Спочатку розглянемо випадок двох паралельних сил
Доповнимо систему сил
Таким чином, вихідна система паралельних сил Визначимо положення лінії дії рівнодіючої Віднесемо тверде тіло до декартової системи координат
Точку Перейдемо тепер до випадку, коли на тверде тіло діє довільна система паралельних сил
Продовживши описаний процес спрощення системи паралельних сил
Точку Розглянемо тепер випадок довільної системи паралельних сил. Її можна собі представляти у вигляді двох різних однаково спрямованих систем сил. Кожна із систем однаково спрямованих сил еквівалентна одній силі. Тому вихідна система паралельних сил еквівалентна двом паралельним силам, спрямованим у протилежні сторони. Якщо ці сили не рівні за величиною, то їх описаним вище способом можна звести до одної еквівалентної сили. Якщо ж розглянуті дві паралельні сили рівні за величиною, протилежно спрямовані, то їх не можна звести до одної сили. Вони утворюють самостійний елемент статики твердого тіла – пару сил. Пара сил викликає рух обертання твердого тіла в просторі, яке на початку руху перебувало в стані спокою. Нехай
Момент пари сил ( Властивості пар сил характеризують теореми [1]: Теорема 1. Пари сил, розміщені в одній площині, еквівалентні, якщо рівні їх моменти. Інакше: пару сил, що діє на тверде тіло, можна замінити іншою парою сил, розміщеною у тій же площині дії з моментом, що дорівнює моменту першої пари.
Доведення 4Нехай дві пари сил Доведемо, що ці пари сил еквівалентні. Оскільки
то
або
Продовжимо лінії дії сил заданих пар до їх перетину в точках А і В й перенесемо сили Тоді з подібності трикутників Аа1а2 і Bb1b2 випливає, що З подібності трикутників Аа1а2 і АDB
а з подібності трикутників АCD і BED
Відповідно до останніх двох виразів одержуємо
Порівнюючи рівності Таким чином, пара Оскільки положення пари - переносити в будь-яке місце у площині дії пари; - повертати плече пари на будь-який кут у площині дії пари; - змінювати довжину плеча і модулі сил пари так, щоб величина моменту пари при цьому не змінювалась. Дія пари на тверде тіло цілком характеризується її моментом, і щоб задати пару, що лежить у заданій площині, досить задати момент цієї пари. Якій величині при цьому дорівнюють сили пари або її плече і де місце розміщення пари в площині її дії – не є істотним. Теорема 2. Пари сил у просторі еквівалентні, якщо рівні їх моменти. Інакше: дія пари сил на тверде тіло не змінюється від перенесення цієї пари сил у паралельну площину.
Нехай дані дві пари сил Доведення 4Візьмемо в площині II відрізок CD, рівний і паралельний відрізку АВ, і у точках C і D прикладемо дві системи зрівноважених (еквівалентних нулю) сил
Складемо сили
прикладені в точці О перетину діагоналей прямокутника ABCD, рівні за модулем і спрямовані по одній прямій у протилежні боки. Тоді сили Оскільки справедлива рівність
то пара З доведеної теореми випливає, що пару сил, не змінюючи її дії на тіло, можна: - переносити в будь-яку площину, паралельну площині її дії; - змінювати плече і силу пари, не змінюючи при цьому величини моменту пари. Отже, при паралельному перенесенні вектора моменту пари сил у будь-яку точку тіла дія пари сил на тверде тіло не зміниться. Таким чином, момент пари сил є вільний вектор, тобто характеризується тільки модулем і напрямком, а точкою прикладення моменту пари може бути будь-яка точка твердого тіла, на яке діє пара сил. Вектор моменту пари сил визначає всі три її елементи: положення площини дії пари, напрямок обертання і числове значення моменту.
Таким чином, механічний вплив у статиці твердого тіла характеризується трьома типами векторів: силою – ковзним вектором, моментом сили відносно точки і парою сил – вільним вектором. Теорема 3. Дві пари, розміщені у площинах, які перетинаються, еквівалентні одній парі з моментом, що дорівнює сумі моментів даних пар. Нехай дві пари сил Доведемо, що дві пари, які діють на тверде тіло, можна замінити однією еквівалентною парою – рівнодіючою парою, яка чинила б на тіло таку саму дію, як і вся система двох пар.
Доведення. 4Приведемо обидві пари до одного спільного плеча АВ, розміщеного на лінії перетину площин I і II. Перетворені у такий спосіб пари позначимо
Склавши за правилом паралелограма сили, прикладені в точках А і В, одержимо
Отже,
і сили
або
тобто теорема доведена: момент еквівалентної пари дорівнює сумі моментів пар, що додаються. 3 Отже, щоб скласти дві пари, що розміщені в площинах, які перетинаються, необхідно скласти їх моменти за правилом паралелограма у будь-якій точці тіла. Помітимо, що отриманий результат справедливий і для пар, розміщених у паралельних площинах і. Зокрема, в одній площині (згідно з теоремою 2 пари, що розміщені в паралельних площинах, попередньо можна перенести в одну площину). Установлене правило складання моментів пар сил називається правилом паралелограма моментів. Згідно з цим правилом можна розв’язати і зворотну задачу, тобто розкласти будь-яку пару сил на дві складові пари. А застосовуючи послідовно правило паралелограма до кожних двох моментів пар, можна будь-яку кількість пар замінити однією, еквівалентною заданій системі пар, - рівнодіючою парою. Нехай дана система
Таким чином, система пар зводиться до однієї пари, момент якої дорівнює векторній (геометричній) сумі моментів усіх пар. Для пар, розміщених в одній площині, правило їх складання формулюється як окремий випадок попереднього: пари, що діють на тверде тіло і розміщені в одній площині, можна звести до однієї пари, алгебраїчний момент якої дорівнює сумі алгебраїчних моментів пар, які складаються, тобто
Так само складаються і пари сил, які розміщені в паралельних площинах, тому що всі ці пари попередньо можна перенести в одну площину. Підіб'ємо підсумок сказаному про систему паралельних сил: довільна система паралельних сил еквівалентна або одній силі, або парі сил. Ознайомимося тепер з поняттям центру ваги тіла й опишемо способи його визначення. Якщо розміри твердого тіла малі в порівнянні з радіусом Землі ( Центр системи паралельних сил ваги всіх малих частинок тіла називають центром ваги тіла. Якщо тіло віднести до декартової системі координат з осями
Тут
На практиці для визначення положення центру ваги тіла користуються такими способами: Спосіб симетрії. Якщо тіло має центр, вісь або площину матеріальної симетрії, то центр ваги такого тіла знаходиться в центрі матеріальної симетрії, на осі матеріальної симетрії або в площині матеріальної симетрії. Дійсно, нехай тіло має площину матеріальної симетрії. Не обмежуючи загальності міркувань, будемо вважати, що ця площина є площиною Приклад 1. Визначити центр тяжіння однорідного колового циліндра радіусу R і висоти h.
Розв’язання. Однорідний коловий циліндр має вісь матеріальної симетрії, яка проходить через центри основ циліндра, та площину матеріальної симетрії, яка проходить через середину висоти паралельно основам. Отже центр тяжіння знаходься одночасно на висоті циліндра та на площині симетрії, тобто на середині висоти.
Спосіб розбивки. Якщо тіло можна мислено розбити на скінчене число частин, центри ваги яких відомі, то координати центру ваги вихідного тіла можна визначити за формулами (3.3). У цих формулах тепер Приклад 2. Визначити центр тяжіння плоскої однорідної пластинки.
Розв'язання. Скористаємось способом розбивки (дивись рисунок). Позначимо через
Для другої частини пластинки:
Отже
Оскільки пластинка має вісь матеріальної симетрії, то Отже координати центра ваги пластинки такі:
Спосіб від’ємних мас. Розглянемо тіло, яке має декілька вирізів, причому відомі маси вирізаних частин тіла й координати центрів ваг цих вирізів. Заповнимо мислено вирізи вилученими частинами тіла, потім розіб'ємо реконструйоване тіло на частини (у число частин обов'язково повинні входити усі вирізи), після цього для визначення координат центру ваги вихідного тіла скористаємося формулами (3.3), але в цих формулах маси вирізів треба вважати від’ємними. Пояснимо сказане прикладом. Визначимо центр ваги круглої однорідної пластинки радіуса
Позначимо буквою
Очевидно, що вісь Теорема Гульдіна. Об'єм тіла обертання однорідної плоскої фігури навколо осі, яка лежить у площині фігури й не перетинає фігуру (торкання дозволяється), дорівнює добутку площі фігури на довжину кола, яке описує її центр ваги при обертанні навколо осі.
Приклад. Визначимо за допомогою теореми Гульдіна положення центру ваги півкругу радіуса
Оскільки вісь
Звідси знаходимо шукану координату
Отже, центр ваги півкруга знаходиться у точці з координатами
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.234.141 (0.155 с.) |
 . Доведемо, що така система сил еквівалентна або одній силі, або двом паралельним силам, рівним за величиною і протилежно спрямованим.
. Доведемо, що така система сил еквівалентна або одній силі, або двом паралельним силам, рівним за величиною і протилежно спрямованим. , спрямованих в одну сторону. Нехай
, спрямованих в одну сторону. Нехай  – точка прикладання сили
– точка прикладання сили 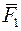 , а
, а  – точка прикладання сили
– точка прикладання сили  .
.
 , які рівні за величиною й протилежно спрямовані уздовж прямої
, які рівні за величиною й протилежно спрямовані уздовж прямої 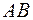 . За аксіомою 1 система сил
. За аксіомою 1 система сил  , що прикладені до точки
, що прикладені до точки  , прикладеної до точки
, прикладеної до точки 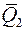 , що прикладені до точки
, що прикладені до точки  , прикладеної до точки
, прикладеної до точки  , є збіжною й, отже, еквівалентна одній силі
, є збіжною й, отже, еквівалентна одній силі =
=  +
+  ==
==  =
=  .
. (рівнодіючої). Вона паралельна силам
(рівнодіючої). Вона паралельна силам  . Ясно, що лінія дії сили
. Ясно, що лінія дії сили  перетину ліній дії сил
перетину ліній дії сил  перетину лінії дії рівнодіючої
перетину лінії дії рівнодіючої  й
й  трикутнику зі сторонами
трикутнику зі сторонами  й
й  випливає, що
випливає, що  . Аналогічно,
. Аналогічно,  . Оскільки
. Оскільки  , із двох останніх рівностей випливає висновок: точка
, із двох останніх рівностей випливає висновок: точка  , або у векторній формі
, або у векторній формі  .
. . Нехай у цій системі координат точка
. Нехай у цій системі координат точка  ,
,  ,
,  , а точка
, а точка  ,
,  ,
, 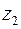 . Визначимо координати
. Визначимо координати  точки
точки  ,
,  ,
,  . Із цих рівностей легко визначимо
. Із цих рівностей легко визначимо


 називають центром системи паралельних сил
називають центром системи паралельних сил  цієї системи. Систему двох паралельних однаково спрямованих сил
цієї системи. Систему двох паралельних однаково спрямованих сил 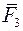 , прикладених до точок тіла
, прикладених до точок тіла  , яка прикладена в центрі
, яка прикладена в центрі  системи паралельних сил
системи паралельних сил  :
: ,
, ,
, 
 , прикладеної до точки тіла
, прикладеної до точки тіла  ,
,  ,
, (3.1)
(3.1) називають центром системи однаково спрямованих паралельних сил
називають центром системи однаково спрямованих паралельних сил  вихідної системи паралельних сил.
вихідної системи паралельних сил. – буквою
– буквою  , який називають моментом пари.
, який називають моментом пари.
 пари сил
пари сил  .
.
 і
і  розміщені в одній площині з рівними моментами.
розміщені в одній площині з рівними моментами.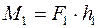 ;
; 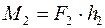 ;
; 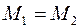 ,
,
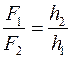 .
. й
й  у ці точки. Відповідно до правила паралелограма розкладемо кожну з цих сил на складові, спрямовані по лінії АВ і лініях дії сил пари
у ці точки. Відповідно до правила паралелограма розкладемо кожну з цих сил на складові, спрямовані по лінії АВ і лініях дії сил пари  і
і  являють собою зрівноважені сили, відкинувши які одержуємо пару
являють собою зрівноважені сили, відкинувши які одержуємо пару  з плечем
з плечем  , яка еквівалентна парі
, яка еквівалентна парі  .
.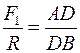 ,
, .
. .
. рівні за модулем силам заданої пари
рівні за модулем силам заданої пари 
 ,
,  і
і  ,
,  , рівних за модулем і паралельних силам пари
, рівних за модулем і паралельних силам пари  .
. ;
; 
 і
і  як зрівноважені можна відкинути. Із зазначеного виходить, що пара
як зрівноважені можна відкинути. Із зазначеного виходить, що пара 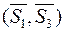 , але розміщеною в паралельній площині II.
, але розміщеною в паралельній площині II. ,
, і
і  мають моменти
мають моменти  і
і 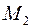 (відповідно) та розміщені у площинах I і II,які перетинаються (див. рисунок нижче). Випадки, коли пари лежать в одній або паралельних площинах, є окремими випадками того, що розглядається.
(відповідно) та розміщені у площинах I і II,які перетинаються (див. рисунок нижче). Випадки, коли пари лежать в одній або паралельних площинах, є окремими випадками того, що розглядається.
 . При цьому повинні виконуватися рівності
. При цьому повинні виконуватися рівності ,
,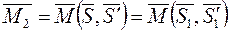 .
.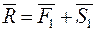 ;
; 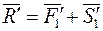 .
.


 ,
, пар
пар  , довільно розміщених у просторі з моментами
, довільно розміщених у просторі з моментами  ,
,  ,...,
,...,  відповідно. Переносячи моменти пар у будь-яку точку О простору і послідовно їх складаючи, можна побудувати многокутник моментів пар, замикаюча сторона якого являє собою момент
відповідно. Переносячи моменти пар у будь-яку точку О простору і послідовно їх складаючи, можна побудувати многокутник моментів пар, замикаюча сторона якого являє собою момент  пари, яка є еквівалентною даній системі пар:
пари, яка є еквівалентною даній системі пар: .
. .
.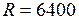 км.), то сили тяжіння його частинок до центру Землі можна практично вважати системою паралельних сил, спрямованих вертикально вниз.
км.), то сили тяжіння його частинок до центру Землі можна практично вважати системою паралельних сил, спрямованих вертикально вниз. , то координати його центру ваги
, то координати його центру ваги  ,
,  ,
, (3.2)
(3.2) – координати
– координати 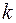 - тої частинки тіла,
- тої частинки тіла, 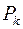 – її вага. Оскільки
– її вага. Оскільки 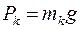 , то у формулах (3.2) сили ваги
, то у формулах (3.2) сили ваги  можна замінити масами частинок
можна замінити масами частинок 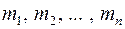 і одержати інші формули для координат центру ваги тіла, більш зручні для застосувань
і одержати інші формули для координат центру ваги тіла, більш зручні для застосувань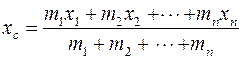 ,
,  ,
, . (3.3)
. (3.3) введеної нами декартової системи координат
введеної нами декартової системи координат  існує така ж частка, симетрично розташована відносно зазначеної площини, яка має таку ж масу як вихідна частка й координату
існує така ж частка, симетрично розташована відносно зазначеної площини, яка має таку ж масу як вихідна частка й координату  . Отже, якщо тіло має площину матеріальної симетрії
. Отже, якщо тіло має площину матеріальної симетрії  , то частці маси
, то частці маси  з координатами
з координатами  , яка не лежить у площині матеріальної симетрії, буде відповідати частка такої ж маси
, яка не лежить у площині матеріальної симетрії, буде відповідати частка такої ж маси  . Якщо ж частка лежить у площині матеріальної симетрії, то її координата
. Якщо ж частка лежить у площині матеріальної симетрії, то її координата  можна розбити на пари, які відповідають симетричним часткам (з координатами
можна розбити на пари, які відповідають симетричним часткам (з координатами  , тобто центр ваги тіла знаходиться в площині матеріальної симетрії тіла. Аналогічно доводяться інші твердження для способу симетрії.
, тобто центр ваги тіла знаходиться в площині матеріальної симетрії тіла. Аналогічно доводяться інші твердження для способу симетрії.
 – число частин, на які розбито тіло,
– число частин, на які розбито тіло,  , координати точок прикладання яких відомі:
, координати точок прикладання яких відомі: 

 масу одиниці площі матеріалу пластинки, тобто її щільність. Для першої частини пластинки:
масу одиниці площі матеріалу пластинки, тобто її щільність. Для першої частини пластинки: ,
,  ,
,  .
. ,
,  ,
,  .
.
 .
. .
. ,
,  .
. , яка має виріз радіуса
, яка має виріз радіуса  . Центр вирізу знаходиться на відстані
. Центр вирізу знаходиться на відстані 
 щільність пластинки, тобто масу одиниці площі пластинки. Початок осі
щільність пластинки, тобто масу одиниці площі пластинки. Початок осі 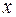 декартової системи координат помістимо в центр суцільного кола й спрямуємо вісь
декартової системи координат помістимо в центр суцільного кола й спрямуємо вісь  , а координата центру ваги вирізу
, а координата центру ваги вирізу  . Розглядувану пластинку з вирізом можна вважати складеною із двох частин: суцільної пластинки й вилученої з неї круглої пластинки. Маса суцільної пластинки
. Розглядувану пластинку з вирізом можна вважати складеною із двох частин: суцільної пластинки й вилученої з неї круглої пластинки. Маса суцільної пластинки 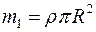 , маса вирізаної пластинки
, маса вирізаної пластинки  . За способом від’ємних мас координата
. За способом від’ємних мас координата  центру ваги пластинки з вирізом обчислюється за формулою
центру ваги пластинки з вирізом обчислюється за формулою

 . Отже, центр ваги розглянутої круглої однорідної пластинки із круглим вирізом знаходиться в точці з координатами
. Отже, центр ваги розглянутої круглої однорідної пластинки із круглим вирізом знаходиться в точці з координатами  ,
, 
 .
.
 декартової системи координат
декартової системи координат 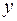 уздовж діаметру так, щоб система координат
уздовж діаметру так, щоб система координат 
 , а довжина кола, яке опише центр ваги
, а довжина кола, яке опише центр ваги  . Згідно з теоремою Гульдіна
. Згідно з теоремою Гульдіна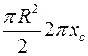 .
. .
. ,
, 


