
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Алгебра высказыванийСтр 1 из 6Следующая ⇒
Глава 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ ПОНЯТИЕ ВЫСКАЗЫВАНИЯ Основные понятия алгебр высказываний и предикатов – утверждение, высказывание и предикат. Утверждение – это формализация повествовательного предложения естественного языка. Высказывание – это утверждение, про которое можно сказать истинно оно или ложно, но ни то и другое одновременно. Истинному высказыванию придается значение T (T rue – истина), а ложному – F (F alse – ложь). Пример 1 Предложения: 1) «Волга впадает в Черное море» – высказывание ложно (его истинностное значения F); 2) «Волга впадает в Каспийское море» – высказывание ложно; 3) « 4) «Когда идет дождь, небо покрыто тучами» – высказывание истинно; 5) «Если натуральное число 81 делится на 9, то оно делиться и на 5» – высказывание ложно; 6) «Какой сегодня день?» – не высказывание, так как это вопросительное предложение; 7) «Пусть живет дружба!» – не высказывание, так как это восклицательное предложение.∎ Высказывание будем обозначать большими буквами латинского алфавита Высказывания разделяются на простые (атомы) и составные (молекулы). Простым высказываниям соответствуют простые повествовательные предложения, составным высказываниям – сложные предложения. Пример 2 Высказывания 1, 2, 3 (см. пример 1.1) – простые высказывания, а высказывания 4, 5 – составные. Сложные повествовательные предложения естественного языка образуются из простых предложений с помощью союзов и оборотов, а соответствующие им составные высказывания составляются из простых высказываний с помощью логических связей (логических операций) (табл. 1).
Таблица 1. Логические связки логики высказываний
В алгебре предикатов не существенен конкретный смысл высказываний, а только их значения (
АЛГЕБРА ВЫСКАЗЫВАНИЙ Алгеброй высказываний называется множество Отрицанием высказывания
Отрицание по определению – унарная операция. В естественном языке данной логической операции соответствует отрицание, которое может иметь разные синтаксические выражения. Пример 1 Пусть Конъюнкцией (логическим произведением) высказываний
Эта логическая операция соответствует союзу «и» естественного языка: « Пример 2 Записатьформулой алгебры высказываний предложение естественного языка: «6 делится на 3 и 10 больше 5». Выполнение. Введем атомы: Дизъюнкцией высказываний
Эта логическая операция соответствует союзу «или» естественного языка: « Пример 3 Записатьформулой алгебры высказываний повествовательное предложение естественного языка: «6 делится на 3 или 10 больше 15». Выполнение. Введем атомы: Импликацией двух высказываний
Эта логическая операция в естественном языке представлена такими оборотами: «если В импликации Пример 4 Высказывание «Если натуральное число 16 делится на 4, то оно четное» можно представить формулой Пример 5 Высказывание «Если натуральное число 32 делится на 8, то оно нечетное» можно представить формулой Пример 6 Высказывание «Если натуральное число 32 делится на 7, то оно четное» можно представить формулой Эквивалентностью двух высказываний
В естественном языке эквивалентности соответствуют «тогда и только тогда», «эквивалентно», «все равно что….», «тождественно» и т. п. Пример 2 Высказывание «Изучение информатики будет успешным тогда и только тогда, когда будет усвоена математическая логика» можно представить формулой Выражения · Атом – формула; · Если · Никаких формул, кроме порожденных формул указанными выше правилами, не существует. Если формула Пример 2
Приписывание истинностных значений атомам, входящих в высказывание называется интерпретацией высказывания. Для высказывания, содержащего Операции алгебры логики на множестве · атомы алгебры высказываний соответствуют логическим переменным алгебры логики; · истинностные значения высказываний F и T соответствуют логическим значениям 0 и 1; · формулы алгебры высказываний соответствуют формулам алгебры логики; · интерпретации высказывания алгебры высказываний соответствуют словам алгебры логики и т. д.
Это дает возможность, например, вычисление значения формулы алгебры высказываний, привести к вычислению логичного значения соответствующего выражения алгебры логики Пример 2 Задана формула алгебры высказываний
Вычислить истинностное значение этой формулы с использованием соответствующей формулы алгебры логики если Выполнение. Сопоставим атомам
Вычисление по формуле. 1) 2) 3) 4) 5) 6) Ответ: ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1 Упражнение 1. Среди следующих предложений естественного языка выделить высказывания, определить, истинные они, или ложные. 1) Река Днепр впадает в Черное море. 2) Любой человек имеет брата. 3) Пейте томатный сок! 4) Ни один человек не весит больше 10000 кг. 5) Существует человек младше своего отца. 6) Где твоя чашка? 7) 8) Для любых действительных чисел 9) 10)Любое действительное число 11) 12)При 13)Не существует Выполнение. 1) Да, это высказывание, оно истинно. 2) Да, высказывание ложно. 3) Нет, это восклицательное предложение. 4) Да, высказывание истинно. 5) Да, оно ложно. 6) Нет, это вопросительное предложение. 7) Да, высказывание ложное. 8) Да, высказывание истинно. 9) Да, высказывание ложно, 10) Да, высказывание ложно. 11) Нет, не высказывание. Это алгебраическое выражение. 12) Да, высказывание истинно. 13) Да, высказывание истинно. Упражнение 2. Записать формулами алгебры высказываний такие высказывания. 1) 45 кратное 3 и 42 кратное 3. 2) 45 кратное 3 и 12 не кратное 3; 3) 4) 5) Если число 212 делится на 3 и 4, то оно делится и на 12; 6) Число 212 – трехзначное число, которое делится на 3 и 4. Выполнение. 1) Атомы: 2) Атомы: 3) Атомы: 4) Атом 5) Атомы: 6) Атомы:
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Какие из утверждений – высказывания? 1) Нью-Йорк – столица Канады; 2) Лондон – город на правом берегу Дона; 3) Студент физико-математического факультета;
5) 5 – логическое значение;
Пример 1 Пытаясь вспомнить победителей турнира прошлого года, пять зрителей, присутствующих на турнире, заявили: 1) Антон был вторым, а Борис – пятым; 2) Виктор был вторым, а Денис – третий; 3) Григорий был первым, а Борис – третий; 4) Антон был третий, а Евгений – шестым; 5) Виктор был третий, а Евгений – четвертым. Впоследствии оказалось, что каждый зритель ошибся в одном из своих высказываний. Как на самом деле распределились места в турнире? Выполнение. Обозначим высказывания зрителей логическими переменными По условию задачи каждый зритель ошибся в одном из своих высказываний, а другое его высказывание – истинно. Поэтому можно записать:
А если это так, то
Раскроем скобки, учитывая, что, например,
Таким образом
А это возможно, если
Таким образом, распределение мест участников в турнире следующее: 1) Григорий; 2) Виктор; 3) Антон; 4) Евгений; 5) Борис; 6) Денис.∎ Пример 2 Было четыре мальчика: Андрей, Кирилл, Дмитрий, Федор. Их фамилии Андриенко, Карп, Демченко, Федун (какая в какого мальчика неизвестно). Известно, что первая буква имен мальчиков не совпадает с первой буквой их фамилий. Кроме того, фамилия Дмитрия не Андриенко. Необходимо определить фамилию каждого мальчика, если известно, что первая буква имени Федуна есть первая буква фамилии мальчика, первая буква имени которого – первая буква фамилии Кирилла. Выполнение. Сопоставим каждому мальчику логическую переменную По условию задачи
Очевидно, что Возможны два случаи: 1) 2) Первый случай, однако, невозможный, потому что при этом Поэтому имеет место второй случай, при котором ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2 Упражнение 1. По подозрению в совершении преступления были задержаны Браун, Джон и Смит. Один из них уважаемый в городе старый человек, второй малоизвестный чиновник и третий известный мошенник. В ходе следствия оказалось, что уважаемый человек всегда говорил правду, известный мошенник всегда лгал, а чиновник в одном случаи говорил правду, в другом – обманывал. Задержанные сказали следующие:
Браун: «Я сделал это, Джон не виновен»; Джон: «Браун не виновен. Преступление совершил Смит»; Смит: «Я не виновен, виновен Браун». Необходимо определить имена троих задержанных, и кто с них виновен, если известно, что преступник один. Выполнение. Высказываниям «Виновен Браун», «Виновен Джон», «Виновен Смит» сопоставим логические переменные
Построим таблицу истинности этой формулы.
Видно, что В результате: Смит – известный махинатор и совершил преступление; Джон – уважаемый в городе старый человек; Браун – малоизвестный чиновник. УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 1. В школе старшеклассникам Андриенку, Константинову, Савину и Давыдову поручили убрать 7-й, 8-й, 9-й, 10-й классы. После проверки оказалось, что 10-й класс убран плохо. Оставшиеся в школе ученики, сообщили: · Андриенко: «Я прибирал 9-й класс, а Савин – 7-й»; · Константинов: «Я убирал 9-й класс, а Андриенко – 8-й»; · Савин: «Я убирал 8-й, Константинов – 10-й». Давыдов ничего не сказал, так как ушел домой до проверки. В дальнейшем оказалось, что каждый ученик в одном из двух высказываний сказал правду, а в другом – солгал. Кто какой класс убирал? 2. На вопрос «Кто с трех студентов изучал математическую логику?» получен верный ответ: «Если изучал первый, то изучал и третий, не верно, что если изучал второй, то изучал и третий». Кто изучал математическую логику? 3. Определить, кто с четырех студентов сдал экзамен, если известно: · если первый сдал, то и второй сдал; · если второй сдал, то третий сдал или первый не сдал; · если четвертый не сдал, то первый сдал, а третий не сдал; · если четвертый сдал, то сдал и первый. 4. Известно, что: · если Петр не видел Николая на улице, то или Николай ходил в кино, или Петр сказал правду; · если Николай не ходил в кино, то Петр не видел Николая на улице, и Николай сказал правду; · если Николай сказал правду, то он или ходил в кино, или Петр солгал. Так ходил ли в кино Николай, или нет? 5. Студентки Валентина, Елена, Светлана, Виктория посещают институт по очереди и ведут общий конспект лекций. Необходимо составить график посещения института на следующую неделю, если: · Понедельник – день самостоятельной работы, в институт не ходит никто, а в субботу необходимо быть всем. · Светлана и Виктория не могут посетить занятия во вторник, через большую загруженность в понедельник. · Если Светлана выйдет в среду, или Виктория – в четверг, то Елена согласится посетить занятие в пятницу. · Если Валентина не пойдет в институт в четверг, то Лена разрешит себе пойти туда в среду. · Если Валентина или Виктория будут в институте в середу, то Светлана сможет пойти в пятницу. · Если Виктория в пятницу пойдет на свадьбу подруги, то Валентина будет вынуждена пойти в институт во вторник, а Светлана – в четверг. 6. Однажды следователю пришлось допрашивать одновременно трех свидетелей: Клода, Жака и Дика. Их показания противоречили одно другому, и каждый из них обвинял кого-то во лжи. · Клод утверждал, что Жак обманывает. · Жак обвинил во лжи Дика. · Дик умолял не верить ни Клоду, ни Жаку. Но следователь быстро вывел свидетелей на чистую воду, не задав при этом ни одного вопроса. Кто из свидетелей говорил правду? 7. Четверо друзей – Антонов, Вехов, Сомов и Деев решили провести каникулы в четырех разных городах – Одессе, Киеве, Ташкенте, Москве. Определить, в какой город должен поехать каждый, при следующих ограничениях. Если Антонов не едет в Москву, то Сомов не едет в Одессу. Если Вехов не едет ни в Москву, ни в Ташкент, то Антонов едет в Москву. Если Сомов не едет в Ташкент, то Вехов едет в Киев. Если Деев не едет в Москву, то и Вехов не едет в Москву. Если Деев не едет в Одессу, то Вехов не едет в Москву. 8. Семья, состоящая с отца, матери и трех дочек – Светланы, Дианы и Елены, купила телевизор. Договорились еще с первого вечера смотреть передачи в соответствии с условиями. Если отец смотрит передачу, то мать делает, то же самое. Дочери Диана и Елена, обе или одна с них смотрит передачу. С двух членов семьи – мать и дочка Светлана – смотрит передачу одна и только одна с них. Дочери Светлана и Диана или обе смотрят телевизор, или не смотрит никто. Если дочь Елена смотрит передачу, то отец и дочь Диана делают то же самое. В каком порядке семья смотрела телевизор? Пример 1 Построить П-схему эквивалентности
Выполнение. П-схема:
∎ Пример 2 Построить П-схему импликации. Выполнение. Учтем, что
П-схема:
∎ Пример 4.3 Построить П-схему для оценки спортивного состязания, в котором судят три судьи. Судья, засчитывающий результат, нажимает кнопку, которая имеется в его расположении, а судья, не засчитывающий результат – не нажимает. Если кнопку нажали не меньше двух судьей, должна загораться лампочка, сигнализируя о том, что результат засчитан. Выполнение. Работа такого устройства описывается булевой функцией трех переменных
По этой таблице запишем СДНФ:
Этой формуле соответствует П-схема:
Эту схему можно упростить. Для этого упростим полученную формулу алгебры логики.
Этой формуле соответствует П-схема:
Эта схема содержит значительно меньше переключателей, чем предыдущая, 5 против 12.∎ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.31.73 (0.18 с.) |
 » – высказывание истинно;
» – высказывание истинно; или большими буквами латинского алфавита с индексами:
или большими буквами латинского алфавита с индексами: 

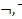




 ).
). , на котором определены логические операции отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности.
, на котором определены логические операции отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности. называется высказывание
называется высказывание  , которое истинно, если
, которое истинно, если 
 высказывание «У Ивана есть время». Тогда высказывание
высказывание «У Ивана есть время». Тогда высказывание  можно представить такими повествовательными предложениями: «Не верно, что у Ивана есть время»; «Не правда, что у Ивана есть время»; «У Ивана нет времени». ∎
можно представить такими повествовательными предложениями: «Не верно, что у Ивана есть время»; «Не правда, что у Ивана есть время»; «У Ивана нет времени». ∎ называют высказывание
называют высказывание  , которое истинно, если оба высказывания
, которое истинно, если оба высказывания 
 : «10 больше 5». Тогда заданное предложение естественного языка можно представить формулой алгебры высказываний
: «10 больше 5». Тогда заданное предложение естественного языка можно представить формулой алгебры высказываний  . Так как
. Так как  и
и 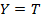 , то и
, то и  , то есть высказывание «6 делится на 3 и 10 больше 5» – истинно.∎
, то есть высказывание «6 делится на 3 и 10 больше 5» – истинно.∎ , которое истинно, если хотя бы одно из высказываний
, которое истинно, если хотя бы одно из высказываний 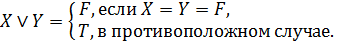
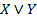 . Так как
. Так как  , то
, то  , то есть высказывание «6 делится на 3 или 10 больше 15» – истинно.∎
, то есть высказывание «6 делится на 3 или 10 больше 15» – истинно.∎ , которое ложно, если высказывание
, которое ложно, если высказывание 
 , где атом
, где атом 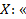 Натуральное число 16 делится на 4», а атом
Натуральное число 16 делится на 4», а атом  , то есть высказывание «Если натуральное число 16 делится на 4, то оно четное» истинно.∎
, то есть высказывание «Если натуральное число 16 делится на 4, то оно четное» истинно.∎ , то есть высказывание «Если натуральное число 32 делится на 8, то оно нечетное» ложно.∎
, то есть высказывание «Если натуральное число 32 делится на 8, то оно нечетное» ложно.∎ : «Натуральное число 32 делится на 7», а атом
: «Натуральное число 32 делится на 7», а атом  : «Натуральное число 32 четное». Так как
: «Натуральное число 32 четное». Так как  ,
,  , которое истинно, если высказывание
, которое истинно, если высказывание 
 , где атом
, где атом 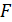 ,
,  ,
,  и
и  – формулы, то
– формулы, то  ,
,  ,
, 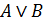 ,
,  ,
,  – также формулы;
– также формулы;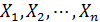 , то будем обозначать ее как
, то будем обозначать ее как  .
. .∎
.∎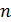 атомов, существует
атомов, существует  интерпретаций.
интерпретаций.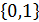 и алгебры высказываний на множестве
и алгебры высказываний на множестве  .
. .
. логические переменные
логические переменные  ,
,  ,
,  соответственно. По условию
соответственно. По условию  ,
,  ,
,  Соответствующая заданной формуле алгебры высказываний формула алгебры логики имеет вид:
Соответствующая заданной формуле алгебры высказываний формула алгебры логики имеет вид: .
.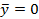 ;
; ;
; ;
; ;
;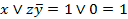 ;
; .
. .∎
.∎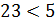 .
. .
. .
.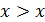 .
. .
. .
. при котором
при котором  .
. .
. и
и  ;
; ;
; и
и  , то
, то  (заданное высказывание истинно).
(заданное высказывание истинно). . Так как
. Так как  (заданное высказывание ложно).
(заданное высказывание ложно). : «число 212 делится на 12». Формула логики высказываний:
: «число 212 делится на 12». Формула логики высказываний:  . Так как
. Так как  ,
, 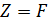 , то
, то  .
. . Так как
. Так как  , то
, то  .
.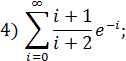


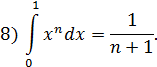
 .
.
 , где
, где  для Антона,
для Антона,  для Бориса,
для Бориса, 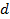 для Дениса,
для Дениса,  для Евгения,
для Евгения, 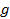 для Григория,
для Григория,  для Виктора), а
для Виктора), а  .
. ,
,  ,
,  ,
,  ,
,  .
. .
. (один участник турнира не может занять два места),
(один участник турнира не может занять два места),  (два участника турнира не могут занять одно место):
(два участника турнира не могут занять одно место):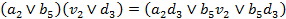 ,
,
 ,
,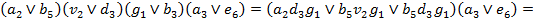
 ,
,
 .
. ,
, ,
,  ,
,  ,
,  ,
,  .
. , где
, где  для Кирилла,
для Кирилла,  для Федора), а
для Федора), а  ,
, 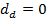 ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, ,
,  ;
; ,
,  ;
; , а по условию задачи
, а по условию задачи  . и в результате фамилии мальчиков следующие: Андрей Демченко, Дмитрий Федун, Кирилл Андриенко, Федор Карп.∎
. и в результате фамилии мальчиков следующие: Андрей Демченко, Дмитрий Федун, Кирилл Андриенко, Федор Карп.∎ ,
,  ,
,  соответственно. Тогда высказывания задержанных можно записать в виде конъюнкций
соответственно. Тогда высказывания задержанных можно записать в виде конъюнкций  ,
,  ,
,  , две из которых, по условию задачи, равны 0, а одна 1. Поэтому можно записать
, две из которых, по условию задачи, равны 0, а одна 1. Поэтому можно записать .
.
 .
.



 .
. . С условия задачи следует, что эта функция задается такой таблицей истинности.
. С условия задачи следует, что эта функция задается такой таблицей истинности.
 .
.



 .
.


