Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет №8 (Линейный оптимальные быстродействия. Теорема для линейных оптимальных быстродействиях) ⇐ ПредыдущаяСтр 3 из 3
Рассмотрим управляемые объекты, движение которых описывается линейными уравнениями относительно величин x1…xn, u1…ur, уравнениями вида, A= B= Для того, чтобы записать эти уравнения в векторном виде, мы ввели в рассмотрение матрицы А и В, элементами которых являются коэффициенты Аналогично для любого r-мерного вектора u=(u1…ur) через Вu обозначается n-мерным вектор, i-я координата которого равна Теорема Пусть u(t)=T, t0<=t<=t1 – допустимое управление переводящее фазовую точку из некоторого положения x0ЭS0 в положение Равновесия. Для оптимального управления u(t) необходимо и достаточно, чтобы оно удовлетворяло принципу максимума
Билет №9 (План решения линейной задачи ОУ) Линейной задачей ОУ мы будем называть задачу об отыскании оптимального быстродействия в случае, когда выполняются три условия: 1. Уравнение движения объекта – линейное 2. Предписанное конечное состояние совпадает с началом координат в пространстве Хn 3. Областью управления U является n-мерный выпуклый многогранник, при этом начало координат принадлежит этому множеству, но не является его вершинами
Систем Система Задача Ψ(t) системы ψ при произвольно заданном начальном значении ψ(t0)= ψ0. Решение этой задачи дается классическими теоремами о линейных ДУ с постоянными коэф. Существуют такие хорошие разработанные приближенные методы решения этой задачи. Так как далее принцип максимума является необходимым условием оптимальности, то всякое управление должно удовлетворять условию максимума. Таким образом в силу принципа максимума в конечном счете траектория x(t) однозначно определяется выбором начального значения ψ0 – даже произвольно, есть шансы что мы попадем в начало координат. Однако при разных ψ0, будут получаться разные траектории, исходящие из x0. Оптимальное управление это такая траектория x(t) при которой u(t) и ψ0 будут проходить через начало координат. Это непосредственно вытекает из того, что если траектория x(t) ведет в начало координат, то принцип максимума является достаточным условием оптимальности. И тогда следующая задача – задача на поиск траектории, приходящей в начало координат. Используем приближенное линейного решения. Взяв произвольное начальное значение ψ0 и улучшаем его так, чтобы траектория, соответствующая этому улучшению проходила через начало координат. Если окажется, что процесс последовательных улучшений сравнительно быстро сходится к требуемому значению, то таким образом мы получаем возможность к приближенному решению.
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.18.87 (0.006 с.) |
 , i=1..n,
, i=1..n, 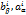 – некоторые постоянные коэффициенты. Одним из наиболее важных случаев, когда u1…ur в уравнениях представляют собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задается неравенством aβ<=uβ<=bβ, где β=1…r, эти неравенства определяет r-мерный параллелепипед.
– некоторые постоянные коэффициенты. Одним из наиболее важных случаев, когда u1…ur в уравнениях представляют собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задается неравенством aβ<=uβ<=bβ, где β=1…r, эти неравенства определяет r-мерный параллелепипед.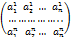

 . Как обычно, результат применения матрицы А к вектору Х будем записывать Ах, т.е. y=Ax есть n-мерный вектор, координаты которого определяются формулами y’=
. Как обычно, результат применения матрицы А к вектору Х будем записывать Ах, т.е. y=Ax есть n-мерный вектор, координаты которого определяются формулами y’= 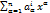 , i=1…n.
, i=1…n. , i=1…u. Пользуясь матрицами A и B мы можем записать
, i=1…u. Пользуясь матрицами A и B мы можем записать 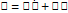
 является системой линейных уравнений с постоянными коэффициентами. В нее не входят переменные xi uj и поэтому система эта решается независимо от всех остальных уравнений
является системой линейных уравнений с постоянными коэффициентами. В нее не входят переменные xi uj и поэтому система эта решается независимо от всех остальных уравнений