
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет №1 (Управляемые объекты. Фазовые траектории. Процесс управления)Стр 1 из 3Следующая ⇒
Ьилет №3 (Допустимые управления. Общая постановка задачи ОУ) Допустимые управления.
Обычно управляющие параметры u1, u2, …, ur не могут принимать произвольные значения, а подчинены некоторым ограничениям. Например, сила u, развиваемая двигателем, не может быть произвольно большой по величине, а подчиняется ограничению:
α ≤ u ≤ β, (6)
где α и β постоянны. Т.к. u – одномерная величина, то все ее значения находятся на действительной оси. Для объекта, содержащего r управляющих параметров, ограничение имеет вид:
α1≤u1≤β1
При r=2, u={u1,u2} – все возможные значения находятся в прямоугольнике. При r=3 – в параллелепипеде, а в общем случае все u1,u2,…,ur принадлежат некоторой области
Предполагается, что мы рассматриваем не только непрерывные функции u(t), но и кусочно-непрерывные. Управление может состоять из конечного числа кусочно-непрерывных управлений. Условимся называть допустимым управлением некую кусочно-непрерывную функцию u(t), все значения которой определены в области
Билет №5 (Принцип максимума для задачи ОУ с закрепленными концами) Следующая теорема (необходимое условие оптимальности ), главным содержанием которой является равенство (22), имеет вид:
Пусть u(t), t0≤t≤t1, такое допустимое управление, что соответствующая ему фазовая траектория
1) при любом t, t0≤t≤t1, функция H(
H( 2) в начальный момент времени t1 , выполнено соотношение ψ0(t1)≤0 и M(
Если максимум функции H(
Билет №6(Принцип максимума для задачи ОУ по быстродействию)
Пример задачи синтеза Рассмотрим уравнение В фазовых координатах: x1 Это уравнение будет иметь следующий вид:
Рассмотрим (для фазовой точки, движущейся по закону (1)) задачу о быстрейшем попадании в начало координат (0,0) из любого заданного начального состояния x0, иначе говоря, мы будем рассматривать задачу об оптимальном быстродействии. Имеем задачу с закрепленными концами. Решение: Функция Гамильтона имеет вид: H=(
Для сопряженных (вспомогательных) переменных
. Это система линейных дифференциальных уравнений с постоянными коэффициентами для сопряженных переменных Рассмотрим решение первого уравнения.
Подставляя,
Проинтегрировав, обе части уравнения получаем:
Соотношение принципа максимума (9) дает нам, учитывая (8) и условия максимума для Подставляем
Находим максимум гамильтониана в любой момент времени, при фиксированных значениях
u=
u(t)=1.
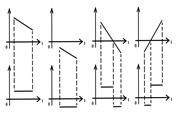
Рис.10
Для данной функции Гамильтона u принимает граничные значения 1,если u(t)= (3) 1,если Такая функция имеет вид: u=sign Из (3) следует, что каждое оптимальное управление u(t), t0≤t≤t1 является кусочно-постоянной функцией принимающей значения
Далее, преступаем к решению системы дифференциальных уравнений для фазовых координат: 1) Для отрезка времени на котором
Получаем:
Преобразуем и получим зависимость:
Это уравнение параболы при заданном s (рис. 11).
Рис.11 Определим направление движения фазовой точки по данным траекториям. По этим параболам (рис. 11) фазовая точка движется снизу вверх, так как
2) Для отрезка времени на котором
Это семейство парабол (рис. 12).
Рис.12
Движение сверху вниз, так как Каждое оптимальное управление u(t) является кусочно-постоянной функцией, принимающей значения
Если управление u(t) сначала, в течение некоторого времени, равнялось +1, а затем стало равно -1, то фазовая траектория движения по двум "кускам" парабол, примыкающих друг к другу, причем второй из этих "кусков" лежит на первой параболе (рис. 13).
Рис.13 Наискорейший путь.
Причем второй из этих "кусков" лежит на параболе (u=-1), которая проходит через начало координат.
Если u равнялось -1, а затем +1, то траектория движения будет (рис. 14).
Все семейство парабол показано на следующем рисунке (рис. 15).
Рис.15
Все семейство точек выше AOB будет смотри (рис. 15).
Область I: Семейство траекторий, ведущее в начало координат, без переключения управления. Область II: Семейство траекторий, ведущее в начало координат, с управлением u=-1. Область III: Для всех точек, находящихся выше линии AOB траектории будут состоять из "куска" траектории с управлением u=-1, до тех пор, пока фазовая точка не попадёт на параболу AO (рис. 15). Область IV: Для всех точек, находящихся ниже линии AOB траектории будут состоять из "куска" траектории с управлением u=1, до тех пор, пока фазовая точка не попадет на параболу BO.
Полученное в рассмотренном примере, решение оптимальной задачи можно истолковать следующим образом. Обозначим v(x1,x2) или v(x), функцию заданную на плоскости, следующим образом.
+1, если ниже линии AOB или на дуге AO. v(x)= -1, если выше линии AOB или на дуге BO.
Тогда на каждой оптимальной траектории значение u(t), управляющего параметра, в произвольный момент времени t равно v(x(t)), то есть равно значению функции v в той точке, в которой в момент времени t находится фазовая точка, пробегающая оптимальную траекторию.
Задача синтеза
Будем рассматривать оптимальную задачу в общей постановке, рассматривая все возможные начальные состояния и каждый раз, предписывая в качестве конечной точки x1 начало координат О. Тогда существует такая функция v(x), заданная в фазовом пространстве x и принимающая значения в области U, что уравнение
определяет все оптимальные траектории, ведущее в начало координат.
Следовательно, оптимальное управление оказывается, естественно, искать не в форме u=u(t), а в форме u=v(x), то есть искомое оптимальное управление в каждый момент времени t зависит лишь от того, в какой точке фазового пространства находится в данный момент фазовая точка.
Если мы уже попали в фазовую точку x, то дальнейшее движение (из точки x в точку O) должно быть оптимальным, по этому значение оптимального управления u(t), в момент прохождения фазового положения x, зависит только от x и не зависит от того в какой точке началось движение и времени, во время которого фазовая точка двигалась из точки x0 в точку x.
функция v(x), дающую оптимальные траектории, будем называть синтезирующей функцией, а задачу нахождения этой функции будем называть задачей синтеза.
Теорема Пусть u(t)=T, t0<=t<=t1 – допустимое управление переводящее фазовую точку из некоторого положения x0ЭS0 в положение Равновесия. Для оптимального управления u(t) необходимо и достаточно, чтобы оно удовлетворяло принципу максимума
Билет №9 (План решения линейной задачи ОУ) Линейной задачей ОУ мы будем называть задачу об отыскании оптимального быстродействия в случае, когда выполняются три условия: 1. Уравнение движения объекта – линейное 2. Предписанное конечное состояние совпадает с началом координат в пространстве Хn 3. Областью управления U является n-мерный выпуклый многогранник, при этом начало координат принадлежит этому множеству, но не является его вершинами
Систем Система Задача Ψ(t) системы ψ при произвольно заданном начальном значении ψ(t0)= ψ0. Решение этой задачи дается классическими теоремами о линейных ДУ с постоянными коэф. Существуют такие хорошие разработанные приближенные методы решения этой задачи. Так как далее принцип максимума является необходимым условием оптимальности, то всякое управление должно удовлетворять условию максимума. Таким образом в силу принципа максимума в конечном счете траектория x(t) однозначно определяется выбором начального значения ψ0 – даже произвольно, есть шансы что мы попадем в начало координат. Однако при разных ψ0, будут получаться разные траектории, исходящие из x0. Оптимальное управление это такая траектория x(t) при которой u(t) и ψ0 будут проходить через начало координат. Это непосредственно вытекает из того, что если траектория x(t) ведет в начало координат, то принцип максимума является достаточным условием оптимальности. И тогда следующая задача – задача на поиск траектории, приходящей в начало координат. Используем приближенное линейного решения. Взяв произвольное начальное значение ψ0 и улучшаем его так, чтобы траектория, соответствующая этому улучшению проходила через начало координат. Если окажется, что процесс последовательных улучшений сравнительно быстро сходится к требуемому значению, то таким образом мы получаем возможность к приближенному решению.
Теорема Фельдбаума Предположим, что многогранник U является r-мерным параллелепипедом и что все собственные значения матрицы A, составленной из коэффициентов уравнений действительны. Тогда в ОУ u(t)=(u1(t)….ur(t) каждая функция uβ(t) где бета = 1…r, кусочнопостоянна, принимает только значения aβ и bβ и aβ<=uβ<=bβ и имеет не более n-1 перключений, где b порядок системы. |A-λE|=0 – полином степени n относительно λ. Корни называют характеристическими или собственными числами А. Если λ – характеристическое число, то существует по крайней мере 1 вектор xНЕ=0, что Ах=λх
Билет №1 (Управляемые объекты. Фазовые траектории. Процесс управления) Понятие об управляемых объектах. Рассмотрим, например, прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля характеризуется двумя числами: путь S, скорость V. Две эти величины меняются в зависимости от времени t, но не самопроизвольно, а сообразно воле водителя, управляющего работой двигателя, увеличивая или уменьшая развиваемую двигателем силу F.
Схема управляемого объекта (рис. 1):
Величины S и V, характеризующие состояние объекта – фазовые координаты, величина F – управляющий параметр.
Если рассматривать движение автомобиля не на прямой, а на плоскости, то фазовых координат будет 4 (2 географические компоненты и 2 компоненты скорости), а управляющих параметров будет 2: мощность двигателя (сила тяги) и угол поворота руля.
У летящего самолета можно рассматривать 6 фазовых координат: 3 географические компоненты и 3 компоненты скорости Vx, Vy, Vz; несколько управляющих параметров: F и φ – величины, характеризующие положение рулей высоты и направления и тягу двигателя.
В электрическом утюге с терморегулятором фазовыми координатами будут сила тока и температура нагрева, а управляющим параметром – положение регулятора.
Таким образом, мы имеем следующее математическое описание управляющего объекта: состояние объекта задается в каждый момент времени числами x1, x2, …, xn, которые называются фазовыми координатами. Движение объекта, с математической точки зрения, заключается в том, что его состояние изменяется с течением времени (x1, x2, …, xn – переменные величины). Движение объекта происходит не самопроизвольно: объектом можно управлять “рулями”, положение которых характеризуется в каждый момент времени r числами: u1, u2, …, ur. Эти числа – управляющие параметры. “Рулями” можно манипулировать – по своему желанию изменять u1, u2, …, ur с течением времени (функция времени).
Предположим, что, зная фазовое состояние объекта в t0 и выбрав управляющие функции u1(t), u2(t), …, ur(t), мы сможем математически точно рассчитать поведение объекта для любых t>t0 и найти x1(t), x2(t), …, xn(t), характеризующие изменение фазовых координат с течением времени. Схема объекта в теории автоматического управления (ТАУ) (рис.2):
u1, u2, …, ur – входные переменные, x1, x2, …, xn – выходные переменные в ТАУ.
Величины {ur} удобно считать координатами некоторого вектора u, который будет называться управляющим вектором. Введем n-мерный вектор x = { x1, x2, …, xn }, заданный в n-мерном пространстве. Это n-мерное пространство, в котором в виде точек изображаются фазовые состояния объекта, называется фазовым пространством.
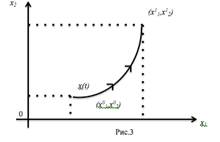
Чтобы полностью задать движение объекта надо задать его начальное фазовое состояние в t0 и выбрать управляющие функции u1(t), u2(t), …, ur(t), t≥t0, т.е. выбрать вектор-функцию u(t) = { u1(t), u2(t), …, ur(t) }. Задав все эти параметры, мы однозначно определяем дальнейшее движение. Оно заключается в том, что фазовая точка x(t) для t>t0 с течением времени перемещается в фазовом пространстве и описывает некоторую линию-траекторию (рис.3).
Пара вектор-функций x(t) и u(t) – процесс управления (или просто - процесс). Билет №2 (Задача управления. Уравнение движения объекта) Часто встречается следующая задача с управляющими элементами: в начальный момент времени t0 – объект находится в фазовом состоянии x0 = { x01, x02, …, x0n }. Требуется выбрать такое управление u(t), t≥t0, которое приведет объект в заранее заданное конечное состояние x1 = { x11, x12, …, x1n }.
Задавая различные управления u(t), t≥t0, получаем множество траекторий x(t).
Множество траекторий.
Обычно требуется, чтобы переходный процесс x0
Если речь идет о наименьшем времени перехода, то такой процесс называется оптимальным в смысле быстродействия.
Уравнения движения объекта.
Начнем с рассмотрения такого примера: пусть G – материальная точка, которая может совершать прямолинейное движение. Ее масса постоянна (рис.4).
Рис.4
Координаты тела G от начала отсчета 0 – x1. При движении такого тела x1 меняется с течением времени, а m
где b – коэффициент трения, k – коэффициент упругости,
Обозначим скорость движения тела x2, тогда закон движения тела G с течением времени описывается следующей системой ДУ первого порядка:
m Величины x1 и x2 – фазовые координаты тела G, а u – управляющий параметр (рис.5).
Эти уравнения представляют собой закон изменения фазовых координат с течением времени, т.е. закон движения тела G (фазовой точки в фазовой плоскости). Движение объекта описывается обыкновенными ДУ. Эти уравнения дают выражение производных от фазовых координат через сами фазовые координаты от управляющих параметров:
или в общем виде:
………………………………
или в векторной форме:
где u, x – векторы.
Эти системы невозможно решить, не зная, каким образом будет меняться u с течением времени. Напротив, зная поведение управляющих параметров u1,u2,…,ur , т.е. зная управляющие функции u1(t), u2(t), …, ur(t), t≥t0, можно с помощью системы:
……………………………………..
однозначно определить движение объекта для t>t0, если известно начальное фазовое состояние t=t0. Задание начального фазового состояния определяет фазовую траекторию x(t), t>t0, с помощью системы (5). Это вытекает из теоремы “О существовании и единственности решения системы ДУ”. Для различных u(t) получаем различные траектории.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.46.36 (0.151 с.) |


 . Множество
. Множество  (t), исходящая в момент времени t0 из точки
(t), исходящая в момент времени t0 из точки  (t) = {ψ0(t),ψ1(t),…ψn(t)}, соответствующей
(t) = {ψ0(t),ψ1(t),…ψn(t)}, соответствующей  ,x(t),u) переменного u
,x(t),u) переменного u  достигает в точке u
достигает в точке u  =u(t) максимума M(
=u(t) максимума M(  (23)
(23) ,где u–вещественное число, удовлетворяющее условию |u|≤1, управляющий параметр.
,где u–вещественное число, удовлетворяющее условию |u|≤1, управляющий параметр. x, x2=
x, x2=  .
. -система двух дифференциальных уравнений первого порядка. (1)
-система двух дифференциальных уравнений первого порядка. (1) ,f), где f1=x2, f2=u,
,f), где f1=x2, f2=u,  ,
,  - вектор-функция, тогда:
- вектор-функция, тогда: . (2)
. (2) и
и  мы получаем систему сопряженных уравнений из Гамильтоновой системы:
мы получаем систему сопряженных уравнений из Гамильтоновой системы: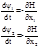

 и
и  .
.
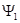 во второе дифференциальное уравнение получаем:
во второе дифференциальное уравнение получаем: .
. .
. u
u  , u(t ) =
, u(t ) =  , из условия максимума.
, из условия максимума. и
и  в (2) получаем:
в (2) получаем:  .
.

 .
. и имеющей не более двух интервалов постоянства (потому что линейная функция
и имеющей не более двух интервалов постоянства (потому что линейная функция  имеет не более одного раза смены знака на интервале от t0 до t1) (рис. 10).
имеет не более одного раза смены знака на интервале от t0 до t1) (рис. 10). . В этом случае имеем следующую систему дифференциальных уравнений
. В этом случае имеем следующую систему дифференциальных уравнений

 , где s1 и s2- постоянные интегрирования.
, где s1 и s2- постоянные интегрирования.
 , где
, где  .
.
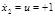 - производная больше нуля, то x2 возрастает для любого t.
- производная больше нуля, то x2 возрастает для любого t. имеем:
имеем:


 .
. , и имеющий не более двух интервалов постоянства (не более одной точки пересечения с осью абсцисс).
, и имеющий не более двух интервалов постоянства (не более одной точки пересечения с осью абсцисс).


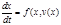

 является системой линейных уравнений с постоянными коэффициентами. В нее не входят переменные xi uj и поэтому система эта решается независимо от всех остальных уравнений
является системой линейных уравнений с постоянными коэффициентами. В нее не входят переменные xi uj и поэтому система эта решается независимо от всех остальных уравнений 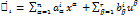


 x1 был наилучшим. Например, чтобы время перехода было минимальным, или расход горючего был минимален, или энергия, затраченная на время переходного процесса, была минимальна, или путь перехода был кратчайшим. Такой наилучший процесс называется оптимальным.
x1 был наилучшим. Например, чтобы время перехода было минимальным, или расход горючего был минимален, или энергия, затраченная на время переходного процесса, была минимальна, или путь перехода был кратчайшим. Такой наилучший процесс называется оптимальным.
 1 – скорость движения тела G. Предположим, что на G действуют две внешние силы: сила трения Fтр. = b
1 – скорость движения тела G. Предположим, что на G действуют две внешние силы: сила трения Fтр. = b 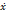 1 и сила упругости Fупр. = -kx1 . Тело G снабжено двигателем. Силу воздействия двигателя обозначим через u. По второму закону Ньютона движение тела G будет описываться следующим дифференциальным уравнением (ДУ) второго порядка:
1 и сила упругости Fупр. = -kx1 . Тело G снабжено двигателем. Силу воздействия двигателя обозначим через u. По второму закону Ньютона движение тела G будет описываться следующим дифференциальным уравнением (ДУ) второго порядка: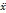 1 = -b
1 = -b 






