
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П. 4. Базис. Розклад вектора за базисом. ⇐ ПредыдущаяСтр 2 из 2
Упорядкована сукупність n лінійно незалежних векторів n -вимірного простору Rn називається базисом, тобто базисом векторного простору називається така система векторів, яка:задана в певному порядку; лінійно незалежна; будь-який вектор простору є лінійною комбінацією цієї системи векторів. Приклади базисів: 1. Базисом на прямій (у R1) є будь-який ненульовий вектор. 2. Базисом на площині (у R2) є два упорядковані неколінеарні вектори. 3. Базисом у тривимірному просторі (R3) є три упорядковані некомпланарні вектори. Якщо базисні вектори взаємно перпендикулярні (ортогональні), базис називають ортогональним. Ортонормованим називають ортогональний базис, утворений одиничними векторами. Якщо вектор
то кажуть, що він розкладений за базисом На рис. 4.9 наведено приклад розкладу вектора
Умови колінеарності та лінійної залежності векторів Через їх координати Два вектори Система векторів
і лінійно залежною, якщо П. 5. Координати вектора на площині та в просторі. Довжина вектора.
Якщо в базисі
Лінійні операції над векторами в базисі Лінійні операції над векторами
Приклад 1. Дано вектори <
Довжина вектора · довжина вектора
· якщо маємо вектора
П.6 Скалярний, векторний та мішаний добутки векторів. Скалярний добуток та його властивості Скалярним добутком двох векторів
Відмітимо, що добуток |
Алгебраїчні властивості скалярного добутку
Геометричні властивості скалярного добутку 1) 2) 3) Скалярний добуток в ортонормованому базисі У базисі
дорівнює сумі добутків їх відповідних координат:
Деякі важливі формули · косинус кута між векторами
· необхідна й достатня умова перпендикулярності двох векторів:
Приклад 2. Вектори 1) < 1) 3)
Приклад 3. Дано вершини трикутника А (1, -3, 0); В (0, -1, –2); < Знайдемо вектори За формулою (4.13) обчислимо косинус кута j між векторами:
Приклад 4. При якому m вектори < Необхідна й достатня умова перпендикулярності двох векторів:
Векторний добуток векторів.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.31.159 (0.012 с.) |
 поданий у вигляді лінійної комбінації базисних векторів:
поданий у вигляді лінійної комбінації базисних векторів: , (4.4)
, (4.4) Вектори
Вектори  називають складовими (компонентами) вектора
називають складовими (компонентами) вектора  - його координатами в базисі
- його координатами в базисі  Зазвичай пишуть так:
Зазвичай пишуть так: 
 Координатами вектора
Координатами вектора  і
і 


 і
і  колінеарні, тоді і тільки тоді коли їх координати пропорційні.
колінеарні, тоді і тільки тоді коли їх координати пропорційні.

 є лінійно незалежною, якщо визначник
є лінійно незалежною, якщо визначник

 У декартовій системі координат базисні вектори, що пов’язані з осями Ox, Oy, Oz, позначають
У декартовій системі координат базисні вектори, що пов’язані з осями Ox, Oy, Oz, позначають  . Якщо
. Якщо  – координати вектора
– координати вектора  в базисі
в базисі  (7.6)
(7.6) за базисом
за базисом  ,
,  ,
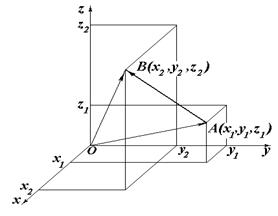
, 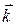 задані координати початку й кінця вектора
задані координати початку й кінця вектора  = (х 2 – х 1)
= (х 2 – х 1) 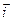 + (у 2 – у 1)
+ (у 2 – у 1)  + (z 2 – z 1)
+ (z 2 – z 1) 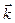 = (х 2 – х 1, у 2 – у 1, z 2 – z 1) (4.5)
= (х 2 – х 1, у 2 – у 1, z 2 – z 1) (4.5)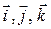
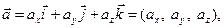
 визначаються так:
визначаються так: (4.6)
(4.6) (4.7)
(4.7) Знайти
Знайти 
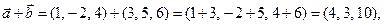

 <
<
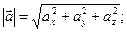 (4.8)
(4.8) (4.9)
(4.9) називається число, що дорівнює добутку довжин векторів на косинус кута j між ними:
називається число, що дорівнює добутку довжин векторів на косинус кута j між ними: (4.10)
(4.10) =|
=|  . (4.11)
. (4.11) 2)
2) 
 4)
4) 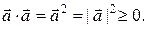
 = 0
= 0  – умова перпендикулярності векторів;
– умова перпендикулярності векторів; – гострий кут;
– гострий кут;
 (4.12)
(4.12)
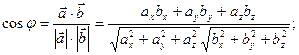 (4.13)
(4.13) Û
Û  (4.14)
(4.14) на вектор
на вектор  (4.15)
(4.15)
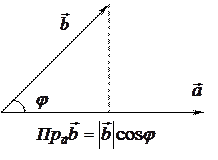
 і
і  утворюють кут
утворюють кут 

 Знайти:
Знайти: 2)
2)  3)
3)  4)
4) 
 2)
2) 

 4)
4)  <
< = (1, –2, 2),
= (1, –2, 2),  = (–1, –1, 4) та їх довжини:
= (–1, –1, 4) та їх довжини: 
 <
< взаємно перпендикулярні?
взаємно перпендикулярні?
 <
<


