
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К выполнению лабораторных работСтр 1 из 3Следующая ⇒
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО АТОМНОЙ ФИЗИКЕ «Изучение спектра и изотопического сдвига (расщепления) линий водорода» Казань 2015
Печатается по решению Редакционно-издательского совета Института физики
УДК 535.3
Р.Х.Гайнутдинов, О.А.Коновалова, Е.В.Сарандаев, М.А.Хамадеев, М.Х.Салахов Методические указания к выполнению лабораторных работ по физике атомных явлений. Учебно-методическое пособие для студентов третьего курса Института физики. Казань, 2015, 28 с.
Учебно-методическое пособие содержит описание и методические указания по выполнению лабораторной работы «Изучение спектра и изотопического сдвига (расщепления) линий водорода» по курсу "Атомная физика” для студентов третьего курса Института физики.
Рецензент: Нефедьев Л.А., д.ф.-м.н., профессор, заведующий кафедрой образовательных технологий Института физики КФУ
Ó Институт физики Казанского федерального университета, 2015. СОДЕРЖАНИЕ
СОДЕРЖАНИЕ. 3 ЦЕЛИ И ЗАДАЧИ РАБОТЫ.. 4 ТЕОРЕТИЧНСКАЯ ЧАСТЬ РАБОТЫ.. 6 Введение. 6 Спектральные серии. 8 Изотопический сдвиг. 10 ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ РАБОТЫ.. 11 Часть I. Определение длин волн линий водорода Ha, Hb и Hg в серии Бальмера. 11 Часть II. Изотопический сдвиг (расщепление) линий водорода. 16 ПРИЛОЖЕНИЕ. 24 ЛИТЕРАТУРА.. 28
ЦЕЛИ И ЗАДАЧИ РАБОТЫ
Цель работы: изучение строения и спектра атомов водорода и дейтерия.
Экспериментальные измерения проводятся на 2-х разных спектральных установках, соответственно, состоят из 2-х частей, в которых решаются следующие задачи: Часть I (первая экспериментальная установка): 1) Визуальное наблюдение при помощи дифракционной решетки высокого разрешения спектральных линий серии Бальмера атома водорода; 2) Измерение длин волн линий водорода Ha, Hb и Hg в серии Бальмера; 3) Определение постоянной Ридберга R∞. Часть II (вторая экспериментальная установка): 1) Измерение длин волн видимых водородных и дейтериевых спектральных линий серии Бальмера. 2) Наблюдение и оценка изотопического расщепления для этих линий. 3) Расчет массы дейтрона (ядро дейтерия), на основании проведенных в пп.1-2 экспериментальных измерений.
Объект исследования: атомы водорода и дейтерия Причина сдвига: При
Рис.1. Сдвиг (расщепление) спектральных линий водорода H, дейтерия D и трития T. Одно из важных следствий наличия сдвига: В s -состоянии атома водорода «электронное облако» сферически симметрично. Наличие изотопического сдвига уровня энергии в этом случае подтверждает, что нельзя электрон в этом состоянии считать «размазанным» по области электронного облака в виде непрерывного распределения его массы.
Особенности физического явления: Сдвиг спектральных линий пропорционален
ТЕОРЕТИЧНСКАЯ ЧАСТЬ РАБОТЫ
Введение
Спектроскопия атома водорода и водородоподобных атомов является очень важным направлением исследований современной физики. На протяжении последних почти 125 лет, начиная с открытия Бальмером в 1885 году серии линий в видимой области спектра, атома водорода, атомная спектроскопия не раз приводила к глобальным переосмыслениям и дополнениям законов физики. Как хорошо известно, попытки объяснения серии Бальмера, а также других спектральных серий, в конечном итоге привели к созданию квантовой механики, которая триумфально описала спектральные серии в спектре атома водорода. Повышение точности измерения частоты переходов в атоме водорода привело к открытию в 1947 году Лэмбом и Резерфордом расщепления 2 S 1/2 и 2 P 1/2 уровней, названного лэмбовским сдвигом. Это открытие послужило мощным стимулом для развития квантовой электродинамики (КЭД) и в целом квантовой теории поля. Теория перенормировок, развитая для объяснения этого сдвига, стала ключевым элементом квантовой электродинамики. По аналогии с КЭД были построены квантовая хромодинамика (КХД) и теория электрослабых взаимодействий, и на основе этих теорий была принята концепция Стандартной модели. Поэтому проверке КЭД на простых водородоподобных атомных системах уделяется большое внимание. Благодаря прогрессу в развитии лазерной спектроскопии удалось с 1997 по 2004 годы измерить с высочайшей точностью оптическую частоту 1 S → 2 S двухфотонного резонанса [1, 2] и оптические частоты 2 S → nS / nD двухфотонных переходов в водороде и дейтерии [3]. В результате для перехода 1 S → 2 S в атоме водорода была достигнута точность измерения с относительной ошибкой порядка 10-14. Благодаря современной прецизионной спектроскопии удалось значительно повысить точность определения постоянной Ридберга и среднеквадратичного зарядового радиуса протона (его часто называют сокращенно радиусом протона). Основоположник современного способа прецизионной лазерной спектроскопии Теодор Хэнш удостоен Нобелевской премии по физике в 2005 г.
Помимо спектроскопии обычных атомов активно развивается спектроскопия мюонных атомов, т.е. атомов, у которых один или несколько электронов заменены мюоном. Эксперименты по лазерной спектроскопии атомов мюонного водорода начались в 2001 году [4] и, как ожидалось, они должны были уточнить значение радиуса протона, полученное из спектроскопии атома водорода. Однако эксперименты были завершены лишь в 2010 году и привели к неожиданным результатам [5]: радиус протона, определенный из анализа данных спектроскопии мюонного водорода, оказался на 4% меньше радиуса, полученного с помощью спектроскопии обычного водорода. Именно поэтому экспериментаторы не наблюдали резонанс, предсказанный на основе данных по спектроскопии атома водорода, и потребовалось достаточно много времени для выяснения причин возможной ошибки. Это расхождение не укладывается в погрешность экспериментов и является также слишком большим, чтобы его можно было устранить путем учета еще нерассчитанных КЭД поправок. Эта проблема является чрезвычайно серьезной, и требуется тщательная проверка всех возможных причин, которые могут приводить к расхождению значений для радиуса протона, начиная с перепроверки точности экспериментов до перепроверки методов, которые используются для описания связанных состояний в КЭД. Если предположить, что в резонансных экспериментах все проанализировано правильно, это будет означать, что в теории может быть потеряно примерно 100 кГц для лэмбовского сдвига 1 S -состояния атома водорода либо примерно 75 ГГц (0.3 мэВ) для частоты перехода 2 S − 2 P атома мюонного водорода. В 2013 году были опубликованы результаты эксперимента [6], которые только увеличили расхождение радиусов, полученных в предыдущих экспериментах. Все это говорит о том, что и по сей день, спектроскопия атома водорода является полем для фундаментальных открытий. Спектр атома водорода всегда привлекал внимание исследователей своей относительной простотой. Наиболее удивительным обстоятельством были целые числа в эмпирической формуле Бальмера для волновых чисел в спектральных сериях атома водорода. После открытия электрона и ядра атома задача об атоме водорода стала принципиальной задачей физики атома, ибо атом водорода является единственным в природе атомом, о котором можно сказать точно: в этом атоме один электрон движется в кулоновском поле одного положительного ядра, зависимость потенциала от расстояния r до ядра точно известна e/r. Именно в силу этого обстоятельства спектр излучения атома водорода стал эффективным полигоном для испытания различных физических моделей и теорий, начиная с атома Бора и первых попыток квантовой механики и кончая современной квантовой электродинамикой.
Бор в своей полуклассической теории объяснил формулу Бальмера ценой введения правила квантования момента импульса атома, постулатов о стационарных состояниях атома и частоте излучения при переходах между ними. Учет движения ядра в атоме позволил с большой точностью вычислить постоянную Ридберга в формуле Бальмера и показал, что различные изотопы должны иметь спектральные линии, отличающиеся по длине волны - изотопический сдвиг. Развитие экспериментальной техники позволило обнаружить тонкую структуру спектральных линий атома водорода. Она была объяснена учетом релятивистской зависимости массы электрона от его скорости и введением принципиально новой характеристики электрона – собственного момента импульса (спина) и собственного (спинового) магнитного момента. Теория тонкой структуры вводит в задачу новый вид взаимодействия – спин-орбитальное взаимодействие и приводит к одинаковой энергии электрона в состояниях с одинаковыми главным квантовым числом n и квантовым числом полного момента импульса j. Однако У. Ю. Лэмбом (Willis Lamb) и Р. Ризерфордом (англ. Robert Retherford) (не путать с Эрне́ст Ре́зерфорд, англ. Ernest Rutherford) показали, что уровень 2 s 1/2 смещен вверх (имеет более высокую энергию) относительно уровня 2 p 1/2. Этот лэмбовский сдвиг обусловлен взаимодействием электрона с вакуумом. Вакуум, согласно современным представлениям, соответствует такому квантовому состоянию материи, в котором отсутствуют реальные частицы и электромагнитные кванты. Это состояние описывается таким образом, что пространство оказывается заполненным виртуальными (еще не рожденными) частицами и «нулевыми колебаниями» электромагнитного поля. Взаимодействием с ними и обусловлен лэмбовский сдвиг. Сверхтонкая структура спектральных линий обусловлена взаимодействием полного (сумма спинового и орбитального) магнитного момента электрона с магнитным моментом ядра.
Наконец, конечный размер протона и связанное с ним отклонение от закона Кулона, приводит к еще более мелкомасштабному сдвигу уровней энергии атома. Перечисленные взаимодействия приводят к расщеплению спектральных линий следующих порядков величин (в порядке перечисления):
l: Dl изотоп.сдв.: Dl тонк.стр.: Dl лэмб: Dl сверх.тонк.: Dl кон.разм.
здесь Спектральные серии. Спектральная серия возникает при разрешенных излучательных квантовых переходах с различных возбужденных уровней энергии k на один и тот же конечный уровень n (n < k) и сходится к границе серии при
где
n = 1 - серия Лаймана; n = 2 - серия Бальмера; n = 3 - серия Пашена; n = 4 - серия Брэкетта; n = 5 - серия Пфунда; n = 6 - серия Хэмфри; Как видно из (1), все спектральные серии атома водорода имеют одинаковую структуру – головная линия в серии (i = 1) имеет наименьшую (в этой серии) длину волны
линии сходятся к конечному пределу при
Рис. 2. Энергетическая структура атома водорода.
Вид спектральной серии изображен на рис. 3.
Рис.3. Вид спектральной серии атома водорода. Изотопический сдвиг
Различие ядер изотопов проявляется в их спектрах. Самый простой из изотопических эффектов – эффект массы – состоит в учете движения ядра, проявляющегося в том, что во всех выражениях для энергии уровней (а значит и для длин волн спектральных линий) фигурирует приведенная масса электрона и ядра:
где Следствием этого являются небольшие отличия параметров, зависящих от массы (энергий, размеров, и т.д.) в атомах различных изотопов одного и того же элемента. Порядок величины относительного изменения любого из этих параметров, например, энергии, очевидно, есть:
Как видно, эффект массы наиболее значителен в легких атомах; для изотопов водорода 1/ A 2 ~ 1; для изотопов элементов конца периодической системы элементов 1/ A 2 ~ 10 -4). Для точного расчета постоянная Ридберга должна быть скорректирована с помощью приведенной массы (2). В результате для водорода получаем:
где
где
Экспериментальная установка 1. Спектральные линии могут наблюдаться только в полностью затемненном помещении; 2. Источник питания лампы Бальмера вырабатывает опасное для жизни высокое напряжение и без лампы имеется доступ к высоковольтным контактам. Поэтомуникогда не включайте источник питания в сеть без установленной в держатель лампы Бальмера.
Схема экспериментальной установки представлена на рис. 4 и 5.
а)
б)
Рис.4. Экспериментальная установка для изучения серии Бальмера в спектре водорода. а) общий вид, б) схематическое изображение. Цифрами на рисунке показаны расстояния от левого края соответствующего универсального зажима до левого края оптической скамьи. Обозначения на схеме: a – лампа Бальмера; b – линза осветителя с фокусным расстоянием 50 мм; c – регулируемая оптическая щель; d – камерная линза с фокусным расстоянием 100 мм; e – дифракционная решетка; f – полупрозрачный экран.
Рис.5. Взаимное расположение решетки Роуланда и полупрозрачного экрана.
Затемнить комнату
2) Подключить VideoCom к компьютеру с помощью кабеля с USB- разъемом. 3) Включить блок питания VideoCom в сеть. 4) Нажимая на VideoCom кнопку «MODE» установить на дисплее режим «Intensity ** 2048, 100%». Другие кнопки VideoCom для этой работы не требуются. 5) Запустить на компьютере программу «VideoCom Intensities». Откроется графическое окно с соответствующими опциями, причем ось OX будет проградуирована в пикселях от 0 до 2048. 6) С помощью кнопки
Рис.10. меню «Calibration/Comparison with Theory»
7) По оси OY задается относительная шкала интенсивностей «Intensity I1». 8) С помощью кнопок 9) Начало измерений запускается с помощью кнопки Ход эксперимента
Рис. 11. Общий вид спектра водородно-дейтериевой лампы.
Для наглядности на рисунке 8 приведен общий вид спектра водородно-дейтериевой лампы, полученный на другом спектрометре (Спектрометр EPP2000 UVN-SR фирмы StellarNet). Как видно, интенсивность спектральных линий серии сильно падает с уменьшением длины волны линии (с увеличением энергии возбуждения верхнего уровня). Этот факт надо учитывать в дальнейшей работе при выборе оптимальной экспозиции и ширины входной щели. Задание1: Для первой (красной) линии серии Бальмера определить изотопический сдвиг:
- Ослабить винт на рейтере с голографической решеткой и вращать рейтер до появления красной линии Бальмера, которая выставляется на середину фотолинейки (ось OX) VideoCom. Для улучшения визуальной идентификации линии первоначальную ширину щели делать более широкой, а затем установить ее примерно равной 0.1 мм.
- Передвигая объектив F = 300 мм и наблюдая на экране монитора красную линию добиться, чтобы она четко расщепилась на 2 составляющие (линии). При необходимости увеличить/уменьшить экспозицию (кнопки
- Увеличить эту область (Zoom, Alt+Z). Если необходимо, можно уменьшить уровень фона с помощью F5 => (Calibration/Comparison with Theory) => (Diffraction Angle) => «Background at Minimum».
- Чтобы улучшить разрешение спектральных линий и уменьшить шум, можно использовать кнопку
- Сохранить полученный спектр можно с помощью кнопки «Save As»
- Определить разницу в углах между максимумами спектральных линий.
- Записать угол между оптическими скамьями и угол голографической решетки. Пример измерения
ПРИЛОЖЕНИЕ ЛИТЕРАТУРА
1. Udem, Th. Phase-Coherent Measurement of the Hydrogen 1S¡2S Transition Frequency with an Optical Frequency Interval Divider Chain / Th. Udem, et. al. // Phys. Rev. Lett. -1997. -V. 79. -P. 2646-2649. 2. Mohr, P.J. CODATA recommended values of the fundamental physical constants: 2006 / J.P. Mohr, B.N. Taylor, D.B. Newell // Rev. of Mod. Phys. -2008. -V. 80. -P. 633-730. 3. de Beauvoir, B. Absolute Frequency Measurement of the 2S¡8S=D Transitions in Hydrogen and Deuterium: New Determination of the Rydberg Constant / B. de Beauvoir, et. al. // Phys. Rev. Lett. -1997. -V. 78. -P. 440-443. 4. Kottmann, F. The Muonic Hydrogen Lamb Shift Experiment at PSI / F. Kottmann, et. al. // Hyper. Interac. -2001. -V. 138. -P. 55-60. 17 5. Pohl, R. The size of the proton / R. Pohl, et. al. // Nature. -2010. -V. 466. -P. 213-217. 6. Antognini, A. Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen / A. Antognini et al. // Science. – 2013. – V. 339. – P. 417
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО АТОМНОЙ ФИЗИКЕ «Изучение спектра и изотопического сдвига (расщепления) линий водорода» Казань 2015
Печатается по решению Редакционно-издательского совета Института физики
УДК 535.3
Р.Х.Гайнутдинов, О.А.Коновалова, Е.В.Сарандаев, М.А.Хамадеев, М.Х.Салахов Методические указания к выполнению лабораторных работ по физике атомных явлений. Учебно-методическое пособие для студентов третьего курса Института физики. Казань, 2015, 28 с.
Учебно-методическое пособие содержит описание и методические указания по выполнению лабораторной работы «Изучение спектра и изотопического сдвига (расщепления) линий водорода» по курсу "Атомная физика” для студентов третьего курса Института физики.
Рецензент: Нефедьев Л.А., д.ф.-м.н., профессор, заведующий кафедрой образовательных технологий Института физики КФУ
Ó Институт физики Казанского федерального университета, 2015. СОДЕРЖАНИЕ
СОДЕРЖАНИЕ. 3 ЦЕЛИ И ЗАДАЧИ РАБОТЫ.. 4 ТЕОРЕТИЧНСКАЯ ЧАСТЬ РАБОТЫ.. 6 Введение. 6 Спектральные серии. 8 Изотопический сдвиг. 10 ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ РАБОТЫ.. 11 Часть I. Определение длин волн линий водорода Ha, Hb и Hg в серии Бальмера. 11 Часть II. Изотопический сдвиг (расщепление) линий водорода. 16 ПРИЛОЖЕНИЕ. 24 ЛИТЕРАТУРА.. 28
ЦЕЛИ И ЗАДАЧИ РАБОТЫ
Цель работы: изучение строения и спектра атомов водорода и дейтерия.
Экспериментальные измерения проводятся на 2-х разных спектральных установках, соответственно, состоят из 2-х частей, в которых решаются следующие задачи: Часть I (первая экспериментальная установка): 1) Визуальное наблюдение при помощи дифракционной решетки высокого разрешения спектральных линий серии Бальмера атома водорода; 2) Измерение длин волн линий водорода Ha, Hb и Hg в серии Бальмера; 3) Определение постоянной Ридберга R∞. Часть II (вторая экспериментальная установка): 1) Измерение длин волн видимых водородных и дейтериевых спектральных линий серии Бальмера. 2) Наблюдение и оценка изотопического расщепления для этих линий. 3) Расчет массы дейтрона (ядро дейтерия), на основании проведенных в пп.1-2 экспериментальных измерений.
Объект исследования: атомы водорода и дейтерия Причина сдвига: При
Рис.1. Сдвиг (расщепление) спектральных линий водорода H, дейтерия D и трития T. Одно из важных следствий наличия сдвига: В s -состоянии атома водорода «электронное облако» сферически симметрично. Наличие изотопического сдвига уровня энергии в этом случае подтверждает, что нельзя электрон в этом состоянии считать «размазанным» по области электронного облака в виде непрерывного распределения его массы.
Особенности физического явления: Сдвиг спектральных линий пропорционален
ТЕОРЕТИЧНСКАЯ ЧАСТЬ РАБОТЫ
Введение
Спектроскопия атома водорода и водородоподобных атомов является очень важным направлением исследований современной физики. На протяжении последних почти 125 лет, начиная с открытия Бальмером в 1885 году серии линий в видимой области спектра, атома водорода, атомная спектроскопия не раз приводила к глобальным переосмыслениям и дополнениям законов физики. Как хорошо известно, попытки объяснения серии Бальмера, а также других спектральных серий, в конечном итоге привели к созданию квантовой механики, которая триумфально описала спектральные серии в спектре атома водорода. Повышение точности измерения частоты переходов в атоме водорода привело к открытию в 1947 году Лэмбом и Резерфордом расщепления 2 S 1/2 и 2 P 1/2 уровней, названного лэмбовским сдвигом. Это открытие послужило мощным стимулом для развития квантовой электродинамики (КЭД) и в целом квантовой теории поля. Теория перенормировок, развитая для объяснения этого сдвига, стала ключевым элементом квантовой электродинамики. По аналогии с КЭД были построены квантовая хромодинамика (КХД) и теория электрослабых взаимодействий, и на основе этих теорий была принята концепция Стандартной модели. Поэтому проверке КЭД на простых водородоподобных атомных системах уделяется большое внимание. Благодаря прогрессу в развитии лазерной спектроскопии удалось с 1997 по 2004 годы измерить с высочайшей точностью оптическую частоту 1 S → 2 S двухфотонного резонанса [1, 2] и оптические частоты 2 S → nS / nD двухфотонных переходов в водороде и дейтерии [3]. В результате для перехода 1 S → 2 S в атоме водорода была достигнута точность измерения с относительной ошибкой порядка 10-14. Благодаря современной прецизионной спектроскопии удалось значительно повысить точность определения постоянной Ридберга и среднеквадратичного зарядового радиуса протона (его часто называют сокращенно радиусом протона). Основоположник современного способа прецизионной лазерной спектроскопии Теодор Хэнш удостоен Нобелевской премии по физике в 2005 г. Помимо спектроскопии обычных атомов активно развивается спектроскопия мюонных атомов, т.е. атомов, у которых один или несколько электронов заменены мюоном. Эксперименты по лазерной спектроскопии атомов мюонного водорода начались в 2001 году [4] и, как ожидалось, они должны были уточнить значение радиуса протона, полученное из спектроскопии атома водорода. Однако эксперименты были завершены лишь в 2010 году и привели к неожиданным результатам [5]: радиус протона, определенный из анализа данных спектроскопии мюонного водорода, оказался на 4% меньше радиуса, полученного с помощью спектроскопии обычного водорода. Именно поэтому экспериментаторы не наблюдали резонанс, предсказанный на основе данных по спектроскопии атома водорода, и потребовалось достаточно много времени для выяснения причин возможной ошибки. Это расхождение не укладывается в погрешность экспериментов и является также слишком большим, чтобы его можно было устранить путем учета еще нерассчитанных КЭД поправок. Эта проблема является чрезвычайно серьезной, и требуется тщательная проверка всех возможных причин, которые могут приводить к расхождению значений для радиуса протона, начиная с перепроверки точности экспериментов до перепроверки методов, которые используются для описания связанных состояний в КЭД. Если предположить, что в резонансных экспериментах все проанализировано правильно, это будет означать, что в теории может быть потеряно примерно 100 кГц для лэмбовского сдвига 1 S -состояния атома водорода либо примерно 75 ГГц (0.3 мэВ) для частоты перехода 2 S − 2 P атома мюонного водорода. В 2013 году были опубликованы результаты эксперимента [6], которые только увеличили расхождение радиусов, полученных в предыдущих экспериментах. Все это говорит о том, что и по сей день, спектроскопия атома водорода является полем для фундаментальных открытий. Спектр атома водорода всегда привлекал внимание исследователей своей относительной простотой. Наиболее удивительным обстоятельством были целые числа в эмпирической формуле Бальмера для волновых чисел в спектральных сериях атома водорода. После открытия электрона и ядра атома задача об атоме водорода стала принципиальной задачей физики атома, ибо атом водорода является единственным в природе атомом, о котором можно сказать точно: в этом атоме один электрон движется в кулоновском поле одного положительного ядра, зависимость потенциала от расстояния r до ядра точно известна e/r. Именно в силу этого обстоятельства спектр излучения атома водорода стал эффективным полигоном для испытания различных физических моделей и теорий, начиная с атома Бора и первых попыток квантовой механики и кончая современной квантовой электродинамикой. Бор в своей полуклассической теории объяснил формулу Бальмера ценой введения правила квантования момента импульса атома, постулатов о стационарных состояниях атома и частоте излучения при переходах между ними. Учет движения ядра в атоме позволил с большой точностью вычислить постоянную Ридберга в формуле Бальмера и показал, что различные изотопы должны иметь спектральные линии, отличающиеся по длине волны - изотопический сдвиг. Развитие экспериментальной техники позволило обнаружить тонкую структуру спектральных линий атома водорода. Она была объяснена учетом релятивистской зависимости массы электрона от его скорости и введением принципиально новой характеристики электрона – собственного момента импульса (спина) и собственного (спинового) магнитного момента. Теория тонкой структуры вводит в задачу новый вид взаимодействия – спин-орбитальное взаимодействие и приводит к одинаковой энергии электрона в состояниях с одинаковыми главным квантовым числом n и квантовым числом полного момента импульса j. Однако У. Ю. Лэмбом (Willis Lamb) и Р. Ризерфордом (англ. Robert Retherford) (не путать с Эрне́ст Ре́зерфорд, англ. Ernest Rutherford) показали, что уровень 2 s 1/2 смещен вверх (имеет более высокую энергию) относительно уровня 2 p 1/2. Этот лэмбовский сдвиг обусловлен взаимодействием электрона с вакуумом. Вакуум, согласно современным представлениям, соответствует такому квантовому состоянию материи, в котором отсутствуют реальные частицы и электромагнитные кванты. Это состояние описывается таким образом, что пространство оказывается заполненным виртуальными (еще не рожденными) частицами и «нулевыми колебаниями» электромагнитного поля. Взаимодействием с ними и обусловлен лэмбовский сдвиг. Сверхтонкая структура спектральных линий обусловлена взаимодействием полного (сумма спинового и орбитального) магнитного момента электрона с магнитным моментом ядра. Наконец, конечный размер протона и связанное с ним отклонение от закона Кулона, приводит к еще более мелкомасштабному сдвигу уровней энергии атома. Перечисленные взаимодействия приводят к расщеплению спектральных линий следующих порядков величин (в порядке перечисления):
l: Dl изотоп.сдв.: Dl тонк.стр.: Dl лэмб: Dl сверх.тонк.: Dl кон.разм.
здесь Спектральные серии. Спектральная серия возникает при разрешенных излучательных квантовых переходах с различных возбужденных уровней энергии k на один и тот же конечный уровень n (n < k) и сходится к границе серии при
где
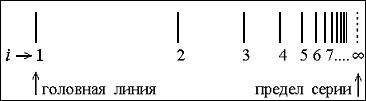
n = 1 - серия Лаймана; n = 2 - серия Бальмера; n = 3 - серия Пашена; n = 4 - серия Брэкетта; n = 5 - серия Пфунда; n = 6 - серия Хэмфри; Как видно из (1), все спектральные серии атома водорода имеют одинаковую структуру – головная линия в серии (i = 1) имеет наименьшую (в этой серии) длину волны
линии сходятся к конечному пределу при
Рис. 2. Энергетическая структура атома водорода.
Вид спектральной серии изображен на рис. 3.
Рис.3. Вид спектральной серии атома водорода. Изотопический сдвиг
Различие ядер изотопов проявляется в их спектрах. Самый простой из изотопических эффектов – эффект массы – состоит в учете движения ядра, проявляющегося в том, что во всех выражениях для энергии уровней (а значит и для длин волн спектральных линий) фигурирует приведенная масса электрона и ядра:
где
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.180.76 (0.197 с.) |
 ядро смещается в противоположную сторону от электрона, и они оба начинают вращаться вокруг общего центра масс. По сравнению с моделью
ядро смещается в противоположную сторону от электрона, и они оба начинают вращаться вокруг общего центра масс. По сравнению с моделью  расстояние между ядром и электроном увеличится, следовательно, энергия взаимодействия уменьшится, что приводит к сдвигу спектральных линий в сторону меньших частот.
расстояние между ядром и электроном увеличится, следовательно, энергия взаимодействия уменьшится, что приводит к сдвигу спектральных линий в сторону меньших частот.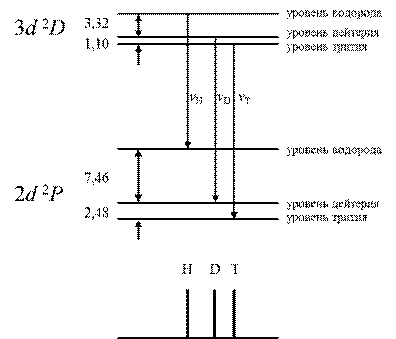
 где
где  – масса электрона,
– масса электрона, 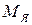 – масса ядра,
– масса ядра,  , поэтому сдвиг достаточно мал, т.к.
, поэтому сдвиг достаточно мал, т.к.  . Отсюда следует, что для экспериментальной регистрации изотопического сдвига требуется спектральный прибор с большой разрешающей силой и большой дисперсией.
. Отсюда следует, что для экспериментальной регистрации изотопического сдвига требуется спектральный прибор с большой разрешающей силой и большой дисперсией.
 : a2: a3: a2
: a2: a3: a2  .
. – масса электрона,
– масса электрона,  – масса протона,
– масса протона,  – постоянная тонкой структуры, определяющая иерархию взаимодействий и расщеплений в атоме.
– постоянная тонкой структуры, определяющая иерархию взаимодействий и расщеплений в атоме.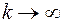 . В соответствии с (16) получается следующее выражение для частоты спектральной линии атома водорода:
. В соответствии с (16) получается следующее выражение для частоты спектральной линии атома водорода: , (1)
, (1) – циклическая частота излучения;
– циклическая частота излучения;  и
и 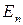 – верхний и нижний уровни энергии. Для каждой спектральной серии число n, определяющее нижний уровень серии, постоянно, а число k, определяющее верхний уровень, равно k = n + i, i = 1,2,3... – номер линии в серии. Переходам на различные нижние уровни соответствуют различные спектральные серии:
– верхний и нижний уровни энергии. Для каждой спектральной серии число n, определяющее нижний уровень серии, постоянно, а число k, определяющее верхний уровень, равно k = n + i, i = 1,2,3... – номер линии в серии. Переходам на различные нижние уровни соответствуют различные спектральные серии: ;
;

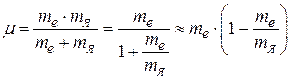 , (2)
, (2) – масса ядра,
– масса ядра,  – масса нуклона, A – массовое число ядра.
– масса нуклона, A – массовое число ядра. . (3)
. (3) , (4)
, (4) , (5)
, (5) – масса нейтрона. Таким образом, спектральные линии серии Бальмера для дейтерия смещаются в сторону более коротких длин волн по сравнению с водородными линиями.
– масса нейтрона. Таким образом, спектральные линии серии Бальмера для дейтерия смещаются в сторону более коротких длин волн по сравнению с водородными линиями.


 или клавиши F5 вызвать меню «Calibration/Comparison with Theory» (см.рис.10.) и в «Diffraction Angle» ввести фокусное расстояние камерной линзы, т.е 300 мм. Закрыть меню, нажав "OK". После этого ось OX будет проградуирована в угловых единицах – в градусах.
или клавиши F5 вызвать меню «Calibration/Comparison with Theory» (см.рис.10.) и в «Diffraction Angle» ввести фокусное расстояние камерной линзы, т.е 300 мм. Закрыть меню, нажав "OK". После этого ось OX будет проградуирована в угловых единицах – в градусах.
 т.е. (-) и (+) задается время экспозиции в относительных единицах от 1 до 8. (обычно 3 бывает достаточно)
т.е. (-) и (+) задается время экспозиции в относительных единицах от 1 до 8. (обычно 3 бывает достаточно) или клавиши F9.
или клавиши F9.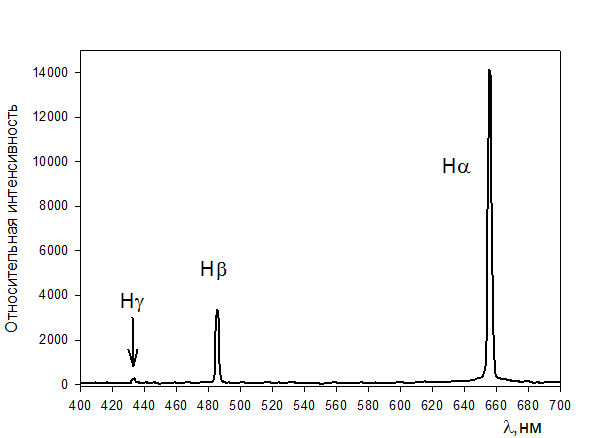
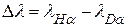 . Сравнить с табличным значением, оценить погрешность измерения.
. Сравнить с табличным значением, оценить погрешность измерения. ) или уменьшить размер щели. На мониторе недалеко от 0° должны наблюдаться два узких максимума различной высоты. Можно более точно выставить линии на 0° с помощью F5 =>(Calibration/Comparison with Theory) => (Diffraction Angle) => (Zero Point Corresponds to Maximum).
) или уменьшить размер щели. На мониторе недалеко от 0° должны наблюдаться два узких максимума различной высоты. Можно более точно выставить линии на 0° с помощью F5 =>(Calibration/Comparison with Theory) => (Diffraction Angle) => (Zero Point Corresponds to Maximum). , с помощью которой происходит усреднение регистрируемых интенсивностей. Когда два максимума можно будет четко различить, то с помощью кнопки
, с помощью которой происходит усреднение регистрируемых интенсивностей. Когда два максимума можно будет четко различить, то с помощью кнопки  или клавиши F9 измерение останавливается.
или клавиши F9 измерение останавливается.


