
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ансамблі та джерела повідомлень
Стан матеріального об’єкта, а отже, і його фізичні показники можуть набувати значення з певного дискретного набору значень. Джерело повідомлень з таким об’єктом є дискретним. Якщо стан матеріального об’єкта, відбитий у його фізичних показниках, набуває значення з нескінченної множини можливих значень, то таке джерело повідомлень є неперервним. Принципово воно може бути зведене до дискретного, якщо прийняти допустимий рівень похибки та за її допомогою з нескінченної множини можливих значень повідомлень вибрати певний дискретний набір. Саме тут у наявності похибки та її допустимому рівні криється принципова різниця між дискретним і неперервним джерелами повідомлень. Якщо під час деякого часового проміжку дискретним джерелом вибрано деяке повідомлення аі, яке ніяк не зумовлене повідомленням аі- 1, вибраним у попередній проміжок часу, то таке джерело є дискретним джерелом без пам’яті. Якщо в деякому часовому проміжку дискретним джерелом вибрано повідомлення аі, пов’язане з попереднім повідомленням аі- 1 статистично зумовлене ним, то таке джерело називається дискретним джерелом із пам’яттю. Крім дискретних, можуть бути також неперервні джерела повідомлень із пам’яттю та без пам’яті. Переліченими тут типами не вичерпуються всі відомі джерела повідомлень. Специфічні джерела повідомлень, в яких враховано статистичні якості фізичних параметрів. Якщо кожного проміжку часу дискретне джерело повідомлень вибирає одне з k можливих повідомлень а 1, а 2,…, аk, то кажуть, що А ={ а 1,…, аk } є дискретною множиною повідомлень, або просто множиною повідомлень А. Як правило, для повнішого опису джерела повідомлень на множині А визначають її ймовірнісну міру, тобто з кожним дискретним повідомленням аі пов’язують ймовірність рі його вибору джерелом. Таки чином, множині А ={ а 1,…, аk } зіставляється ймовірнісна міра у вигляді множини Рk ={ p 1,…, pk }, на яку накладено обмеження у вигляді Дві множини А та Р дають достатньо повний опис дискретного джерела повідомлень у вигляді його ймовірнісної моделі, а тому разом вони утворюють ансамбль повідомлень дискретного джерела. Це означає, що кожного проміжку часу дискретним джерелом вибирається певне повідомлення
Кількісна міра інформації Розгляд дискретного джерела та множини його повідомлень приводить до формулювання таких природних вимог для визначення кількості інформації: 1) у повідомленні про вірогідний випадок вона має дорівнювати нулю; 2) у двох незалежних повідомленнях вона має дорівнювати сумі кількостей інформації в кожному з них; 3) вона не повинна залежати від якісного змісту повідомлення (ступеня його важливості, відомостей тощо). Таким чином, для визначення кількості інформації в повідомленні треба виходити з найзагальнішої його характеристики. Таку характеристику, очевидно, дає модель джерела – ансамбль повідомлень. Звернімо тепер увагу на множину ймовірностей цих повідомлень Для задоволення другої вимоги можна врахувати, що ймовірність двох незалежних повідомлень а 1 та а 2 за законом множення ймовірностей
Звідси випливає необхідність вибору такої функції f(pi), значення якої при перемноженні її аргументів pi додавалися б і щоб f(0)=f(1)=0. Єдиною функцією з такими властивостями є логарифмічна функція
де k – коефіцієнт, який узгоджує розмірності, а логарифм береться за будь-якою зручною основою. При такому визначенні кількості інформації задовольняються всі три наведені вище вимоги. Таким чином, кількість інформації в повідомленні тим більша, чим воно менш ймовірне, тобто більш неочікуване.
Ентропія та її властивості Розглянемо, наприклад, дискретне джерело повідомлень з ансамблем, наведеним у табл. 2.1. Обчислимо, яку кількість інформації несе кожне таке повідомлення, й занесемо ці дані в табл. 2.1. Третій рядок її підтверджує, що кількість інформації при прийнятому її визначенні відображує міру неочікуваності кожного повідомлення.
Таблиця 2.1
Розглянемо, яку кількість інформації несуть більш-менш довгі послідовності таких повідомлень: · перша послідовність а 3, а 1, а 4, а 4, а 2, а 2, а 1, а 3, а 1, а 2, а 5, а 1, а 1, а 2, а 3, а 2, а 1, а 2, а 1, а 1, а 1, а 2, а 1, а 1, а 1, а 2, а 2, а 3, а 4, а 3;
· друга послідовність а 2, а 1, а 3, а 2, а 2, а 1, а 2, а 1, а 3, а 1, а 4, а 2, а 4, а 1, а 1, а 3, а 1, а 2, а 1, а 5. У першій послідовності є 30 повідомлень, а в другій – 20. Розподіл імовірностей з ансамблю (див. табл.2.1.) настільки нерівномірний, що ні до першої, ні до другої послідовностей не ввійшло повідомлення а 6. Справа в тому, що його за законами статистики можна було б помітити в послідовності повідомлень при довжині останньої, значно більшій від n =1/ p 6=50. Отже, кількість інформації в першій послідовності
а в другій
Як бачимо, ці послідовності різняться не тільки кількістю повідомлень, а й кількістю інформації в кожній з них. Однак, якщо обчислити кількість інформації, яка припадає на одне повідомлення в одній послідовності та в іншій, то виявиться, що і 1/30=2,0069 біт/повідомлення та і 2/20=2,0456 біт/повідомлення. Це означає, що середня кількість інформації, яка припадає на одну літеру алфавіту повідомлень (це те саме, що й на одне повідомлення), не залежить від конкретних повідомлень і довжини послідовності їх. Деяка різниця тут між і 1/30 та і 2/20 пояснюється лише недостатньою довжиною послідовностей повідомлень. Відповідно до статистичного закону великих чисел ці відношення збігатимуться краще, чим більшими будуть довжини порівнюваних послідовностей. Можна сказати, що це відношення (тобто кількість інформації, яка припадає на одне повідомлення) характеризує дискретне джерело повідомлень в цілому. Інше джерело з іншим ансамблем повідомлень матиме зовсім іншу питому кількість інформації. Ця загальна характеристика джерела повідомлень називається його ентропією Н (А). Вона має фізичний зміст середньостатистичної міри невизначеності відомостей спостерігача А (див. рис. 2.1) відносно стану спостережуваного об’єкта. Точну ентропію можна визначити як математичне сподівання питомої кількості інформації
Згідно з даними табл. 2.1 маємо Н (А)=0,4·1,322+0,3 Бачимо, що точне значення ентропії Н (А) не дуже відрізняється від значень, здобутих у наведених вище прикладах послідовностей повідомлень. У виразі (2.3) усереднення (як обчислення математичного сподівання) виконується по всьому ансамблю повідомлень. При цьому потрібно враховувати всі ймовірнісні зв’язки між різними повідомленнями. З цього виразу випливає, що чим вища ентропія, тим більшу кількість інформації в середньому закладено в кожне повідомлення даного джерела, тим важче запам’ятати (записати) або передати таке повідомлення по каналу зв’язку. Необхідні витрати на передачу повідомлення пропорційні його ентропії (середній кількості інформації на одне повідомлення). Виходить, що кількість інформації в послідовностях визначається кількістю повідомлень N у послідовності та ентропією Н (А) джерела, тобто
Наприклад, i 1 = 30 · 2,0573 = 61,719 біт; і 2 = 20 · 2,0573 = 41,146 біт. Розбіжність тут пояснюється невеликими значеннями N, адже ймовірність pi обчислюються, як правило, за умови N→∞. Розглянемо вироджене дискретне джерело з єдиним повідомленням Друга властивість ентропії випливає з виразу (2.3), згідно з яким вона є величиною адитивною. Якщо N – вимірні послідовності повідомлень а 1, а 2, … а N розглядати як збільшені повідомлення нового джерела, то його ентропія буде в N разів більшою від початкової. Якщо алфавіт A ={ a 1, a 2, …, ak } має k різних повідомлень, то Н (А) ≤ log k. Тут рівність стосується тільки рівноймовірних і статистично незалежних повідомлень
Безумовна ентропія Термін «безумовна ентропія» запозичений з математичної статистики за аналогією з безумовною ймовірністю, що стосується статистично незалежних подій, тут - повідомлень. Отже, безумовна ентропія - це кількість інформації, яка припадає на одне повідомлення джерела із статистично незалежними повідомленнями. За цим визначенням розглянута в п. 2.3 ентропія є безумовною. Зупинимося докладніше на безумовній ентропії та її властивостях. Якщо є дискретне джерело статистично незалежних повідомлень з ансамблем A ={ a 1, a 2, …, ai, …, ak } та р ={ р 1, р 2, …, рi, …, рk }, то кількість інформації (середня), що припадає на одне повідомлення
є характеристикою цього джерела в цілому. Вона має фізичний зміст середньої за ансамблем невизначеності вибору джерелом повідомлення з А,причому байдуже, якого саме повідомлення, оскільки обчислення ентропії (2.5) «поглинає» індекс і. Наприклад, джерело з k =8 незалежними та рівноймовірними повідомленнями має ентропію
Тут ураховано, що pi = p =1/8. Для нерівноймовірних повідомлень у цьому разі Н (А)< 3 біт/повідомлення. Таким чином, основними властивостями безумовної ентропії дискретних повідомлень є такі: • ентропія - величина дійсна, обмежена та невід'ємна; • ентропія вірогідних повідомлень дорівнює нулю; • ентропія максимальна, якщо повідомлення рівноймовірні та статистично незалежні; • ентропія джерела з двома альтернативними подіями може змінюватися від 0 до 1;
• ентропія складеного джерела, повідомлення якого складаються з часткових повідомлень кількох статистично незалежних джерел, дорівнює сумі ентропії цих джерел. Умовна ентропія Припустимо, що повідомлення а зустрічалося у довгому ланцюзі з N =1000 повідомлень l1 =200 разів, повідомлення b у цьому самому ланцюзі - l 2=200 разів, а разом вони зустрілися лише l 3=50 разів. Скориставшись теорією математичної статистики, можна встановити, що ймовірність появи повідомлення а в цьому ланцюзі р (а) =l 1/ N =0,25, а повідомлення b-p (b)= l 2/ N =0,2. Крім того, р (аb)= l 3/ N =0,05. При цьому p (ab)= p (a) p (b)=0,25·0,2=0,05, що є явною ознакою статистичної незалежності повідомлень а та b. Саме для таких повідомлень існує безумовна ентропія, про яку йшлося вище. Коли б у цьому прикладі пара аb зустрілася l 3=30 разів, то виявилося б, що р (аb)= l 3/ N =0,03< p (a) p (b). Це є ознакою порушення статистичної незалежності повідомлень а та b, яка відбиває той факт, що вони не «прагнуть» зустрічатися разом у послідовностях повідомлень, тобто поява одного з них дає підставу з більшою впевненістю не очікувати появи іншого, ніж це було б до появи першого повідомлення. 3 іншого боку, при l 3=100 маємо р (аb)= l 3/ N =0,1> p (a) p (b), що дає підставу підозрювати взаємне «тяжіння» а до b,і навпаки. Тут теж проглядається порушення статистичної незалежності, тобто відношення «байдужості» між повідомленнями а та b. Мірою порушення статистичної незалежності (стану «байдужості») між повідомленнями а та b є умовна ймовірність появи повідомлення а за умови, що вже з'явилося повідомлення b: p (a / b), або умовна ймовірність появи повідомлення b,коли вже з'явилося повідомлення a: p (b / a), причому взагалі p (a / b)≠ p (b / a). Теорія математичної статистики визначає умовну ймовірність через безумовні ймовірності р (a), p (b)та сумісну безумовну ймовірність р (аb)за законом множення ймовірностей: р (аb) =р (а) р (b/а) =р (b) p (а/b). (2.6) Звідси випливає, що р (b/а) =р (аb) /р (а); р (а/b) =р (аb) /р (b). (2.7) Зокрема, для статистично незалежних повідомлень а та b ( див. вище) маємо р (b/а) = 0,05/0,25=0,2= р (b); р (a/b) = 0,05/0,2=0,25= р (а), тобтоумовні ймовірності появи повідомлень вироджуються в безумовні. Розрізняють два різновиди умовної ентропії: часткову та загальну. Першу знаходять так:
де A ={ a 1, a 2, …, ai, …, ak }, B ={ b 1, b 2, …, bj, …, bl } - алфавіти повідомлень; аі -конкретне повідомлення, відносно якого визначається часткова умовна ентропія Н (В/аi)алфавіту В за умови вибору попереднього повідомлення ai; bj - конкретне повідомлення, відносно якого обчислюється часткова умовна ентропія Н (А/bj)алфавіту А за умови вибору попереднього повідомлення bj; і -номер повідомлення з алфавіту А; j - номер повідомлення з алфавіту В; р (а/b), р (b/а)- умовні ймовірності. Часткова умовна ентропія визначається як статистичне усереднення за методом зваженої суми (2.8), (2.9) по індексу і =1… k або j =1… k відповідно. Ураховуючи викладене вище, загальну умовну ентропію можна визначити так: якщо часткова умовна ентропія джерела А відносно конкретного повідомлення bj дорівнює H (A / bj), а розподіл імовірностей PB джерела B задано ансамблем B із PB ={ p (b 1), …, p (bj), …, p (bk)}, то цілком природно обчислити середнє по j значення H (A / bj) за всіма j як статистичне усереднення методом зваженої суми, тобто
де H (A / B) – загальна умова відносно джерела ентропія джерела А відносно джерела В. Це питома (середньостатистична) кількість інформації, що припадає на будь-яке повідомлення джерела А, якщо відомо його статистичну взаємозалежність із джерелом В. Аналогічно (2.10) загальна умовна ентропія джерела В відносно джерела А визначається виразом
що є питомою (середньостатистичною) кількістю інформації, яка припадає на будь-яке повідомлення джерела В, якщо відомо його статистичну взаємозалежність із джерелом А. Загалом статистична залежність джерела В від джерела А відбивається матрицею прямих переходів повідомлень аі (і= 1... k)джерела А в повідомлення bj (j = 1... k) джерела B:
На головній діагоналі цієї матриці розміщено умовні ймовірності прямої відповідності типу а 1→ b 1 ,..., аk→bk, які характеризують правильний вибір джерелом В своїх повідомлень (тобто відповідно до повідомлень джерела А).Решта ймовірностей відповідають неправильному вибору повідомлень джерелом B. Матриця відбиває вплив завад у каналі між джерелом А та спостерігачем В. Якщо завади непомітні або зовсім відсутні, то маємо однозначну відповідність аi→bi з умовної ймовірності р (bi / аi)=1 для і =1... k. Решта ймовірностей р (bj / аi)=0 для всіх j ≠ i. Кожний рядок у матриці є спотвореним розподілом імовірностей РB появи повідомлення
Статистична залежність джерела А від джерела В відбивається матрицею зворотних переходів типу аі ← bj,складеною з умовних імовірностей p(ai / bi):
Вона відображає k розміщених стовпцями варіантів спотворених первинних розподілів імовірностей ансамблю А, які відчувають на собі статистичний вплив повідомлень bj (j =1… k), вибраних джерелом В. Саме тому для кожного такого розподілу
Нехай задано таку матрицю Р (ai , bj) сумісних імовірностей появи повідомлень двох джерел А та В з алфавітами аi та bj,де i =1, 2,
Оскільки р (аb)- безумовні ймовірності, для них виконується закон нормування
Окрема розгортка по рядках (по i) без зміни j «поглинає» алфавіт аi ідає безумовну ймовірність р (bj),тобто ймовірнісну міру для джерела В (2.17): 0,2 + 0 + 0,1 = 0,3 = р (b1) при j =1; 0 + 0,2 + 0,1 = 0,3 = р (b2) при j = 2; 0,1 + 0,1 + 0,2 = 0,4 = p (b3) при j = 3; Перевіримо нормування: р (b1) + р (b2) + р (b3) = 0,3 + 0,3 + 0,4 = 1. Окрема згортка по стовпцях (за j) без зміни i «поглинає» алфавіт bj і дає безумовну ймовірність р (ai),тобто ймовірнісну міру для джерела А (2.18): 0 + 0,2 + 0,1 = 0,3 = р (a2) при i = 2; 0,1 + 0,1 + 0,2 = 0,4 = p (a3) при i = 3; Перевіряємо нормування: р (a1) + р (a2) + р (a3) = 0,3 + 0,3 + 0,4 = 1. З урахуванням (2.1) на підставі (2.15) дістаємо таку матрицю умовних імовірностей:
Перевірка на виконання закону нормування дає позитивну відповідь, тобто
Отже, кожний рядок (2.16) є розподілом повідомлень ai, спотвореним через статистичний вплив повідомлень
Перевірка виконання закону нормування дає позитивну відповідь, тобто 2/3 + 0 + 1/3 = 3/3=1 = р (b 1 /a 1)+ р (b 2 /a 1)+ р (b 3 /a 1) при i =1; 0 + 2/3 + 1/3 = 3/3=1 = р (b 1 /a 2)+ р (b 2 /a 2)+ р (b 3 /a 2) при i =2; 0,25 + 0,25 + 0,5 =1 = р (b 1 /a 3)+ р (b 2 /a 3)+ р (b 3 /a 3) при i =3. Таким чином, кожний стовпець (2.17) є розподілом повідомлень bj,спотвореним через статистичний вплив повідомлень Тепер, маючи дані (2.16), розрахуємо безумовну ентропію джерела А: Н (А) = - (0,3 lоg 0,3 + 0,3 lоg 0,3 + 0,4 lоg 0,4) = 1,57095 біт/повідомлення. Аналогічно, маючи дані (2.17), обчислимо безумовну ентропію джерела В: Н (В)= - (0,3 lоg 0,3 + 0,3 lоg 0,3 + 0,4 lоg 0,4) = 1,57095 біт/повідомлення. У розглядуваному прикладі Н (В) = Н (А)тому, що збігаються розподіли безумовних імовірностей. До речі, максимального значення Н (А)та H (В)досягли б при рівноймовірному розподілі ймовірностей, тобто при р (ai) = 1/3 та p (bj)= 1/3 для Тоді було б H max(A) = H max(B) = -log (1/ k) = log k = log 3 = 1,58496 біт/повідомлення. Як бачимо, максимальна ентропія перевищує значення безумовної ентропії при нерівномірному розподілі ймовірностей. Часткова умовна ентропія джерела А з урахуванням (2.16) становитиме H (A/b 1) =-[(2/3) lоg (2/3) + 0 lоg 0 + (1/3) lоg (1/3)] = 0,91829 біт/повідомлення; H (A/b 2) =-[0 lоg 0 + (2/3) lоg (2/3) + (1/3) lоg (1/3)] = 0,91829 біт/повідомлення; H (A/b 3) =-(0,25 lоg 0,25 + 0,25 lоg 0,25 + 0,5 lоg 0,5) = 1,5 біт/повідомлення. Загальна умовна ентропія джерела А відносно джерела В H (А/В)= 0,3 H (А/b 1)+ 0,3 H (А/b 2)+ 0,4 H (А/b 3) = 2 · 0,3 · 0,91829 + 0,4 · 1,5= 1,15097 біт/повідомлення. Часткова умовна ентропія джерела В становитиме H (B/a 1) =-[(2/3) lоg (2/3) + 0 lоg 0 + (1/3) lоg (1/3)] = 0,91829 біт/повідомлення; H (B/a 2) =-[0 lоg 0 + (2/3) lоg (2/3) + (1/3) lоg (1/3)] = 0,91829 біт/повідомлення; H (B/a 3) =-(0,25 lоg 0,25 + 0,25 lоg 0,25 + 0,5 lоg 0,5) = 1,5 біт/повідомлення. Загальна умовна ентропія джерела В відносно джерела А H (B/A)= 0,3 · 2 · 0,91829 + 0,4 · 1,5 = 1,15097 біт/повідомлення. Відзначимо окремо такі властивості умовної ентропії: 1. Якщо джерела повідомлень А та В статистично незалежні, H (А/В) = H (А); H (B/A) = H (В). 2. Якщо джерела повідомлень А та В настільки статистично H (А/В) = H (B/A) = 0. 3. Ентропія джерела взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовна ентропія). 4. Максимальну ентропію мають джерела взаємонезалежних рівноймовірних повідомлень, умовна ентропія яких дорівнює нулю, а ймовірність появи символів алфавіту р= 1/ k,де k - кількість повідомлень в алфавіті.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.104 с.) |
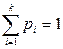 .
.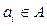 з ймовірністю
з ймовірністю 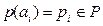 .
. . Якщо йдеться про вірогідний випадок, імовірність якого
. Якщо йдеться про вірогідний випадок, імовірність якого  або
або 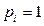 , то кількість інформації в ньому
, то кількість інформації в ньому  , оскільки рівень невизначеності щодо стану об’єкта після вибору джерелом такого повідомлення не змінився. Якщо ж джерело вибере не таке вже наперед визначене повідомлення, то рівень невизначеності щодо стану об’єкта знизиться. Отже, кількість інформації в повідомленні має бути функцією ймовірності цього повідомлення, тобто
, оскільки рівень невизначеності щодо стану об’єкта після вибору джерелом такого повідомлення не змінився. Якщо ж джерело вибере не таке вже наперед визначене повідомлення, то рівень невизначеності щодо стану об’єкта знизиться. Отже, кількість інформації в повідомленні має бути функцією ймовірності цього повідомлення, тобто 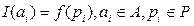 .
.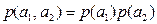 . Проте кількість інформації у цих двох повідомленнях
. Проте кількість інформації у цих двох повідомленнях . (2.1)
. (2.1) , (2.2)
, (2.2) I (ai), біт
I (ai), біт

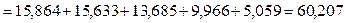 біт,
біт,
 біт.
біт.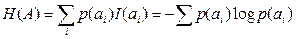 . (2.3)
. (2.3)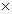 1,737+0,15·2,737+0,1·3,322+0,03·5,059+0,02·5,644=2,0573біт/повідомлення.
1,737+0,15·2,737+0,1·3,322+0,03·5,059+0,02·5,644=2,0573біт/повідомлення. . (2.4)
. (2.4) з р (а)=1. Тоді Н (А)=0 згідно з (2.3). Якщо р (а)=0, то Н (А) теж дорівнюватиме нулю. Таким чином, ентропія завжди додатна або дорівнює нулю, тобто невід’ємна. Це перша її властивість.
з р (а)=1. Тоді Н (А)=0 згідно з (2.3). Якщо р (а)=0, то Н (А) теж дорівнюватиме нулю. Таким чином, ентропія завжди додатна або дорівнює нулю, тобто невід’ємна. Це перша її властивість.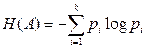 , (2.5)
, (2.5)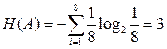 біт/повідомлення.
біт/повідомлення. ; (2.8)
; (2.8) , (2.9)
, (2.9) , (2.10)
, (2.10) , (2.11)
, (2.11) . Джерело В має розподіл безумовних імовірностей РB. Врахування статистичного впливу повідомлення
. Джерело В має розподіл безумовних імовірностей РB. Врахування статистичного впливу повідомлення  спотворює цей розподіл (або уточнює його) і дає новий розподіл імовірностей Р (В/аi)для і -го рядка матриці. Саме тому виконується закон нормування
спотворює цей розподіл (або уточнює його) і дає новий розподіл імовірностей Р (В/аi)для і -го рядка матриці. Саме тому виконується закон нормування , i =1… k. (2. 12)
, i =1… k. (2. 12) (2.13)
(2.13)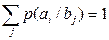 , j =1… k (2.14)
, j =1… k (2.14) (2.15)
(2.15)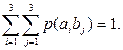
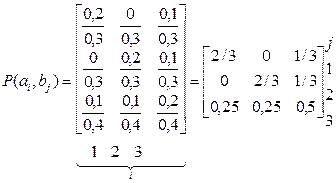 (2.16)
(2.16)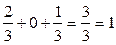 = р (а 1 /b 1)+ р (а 2 /b 1)+ р (а 3 /b 1) при j =1;
= р (а 1 /b 1)+ р (а 2 /b 1)+ р (а 3 /b 1) при j =1; = р (а 1 /b 2)+ р (а 2 /b 2)+ р (а 3 /b 2) при j =2;
= р (а 1 /b 2)+ р (а 2 /b 2)+ р (а 3 /b 2) при j =2; = р (а 1 /b 3)+ р (а 2 /b 3)+ р (а 3 /b 3) при j =3;
= р (а 1 /b 3)+ р (а 2 /b 3)+ р (а 3 /b 3) при j =3;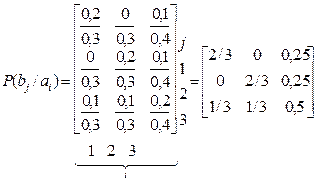 (2. 17)
(2. 17)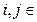 {1,2, 3}.
{1,2, 3}.


