
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные математические ожидания ⇐ ПредыдущаяСтр 3 из 3
Задачи
Винеровский процесс и интегралы Ито Задачи
Решения. Дискретные марковские цепи. 1. а)
б)
в)
2.
3. P( аналогично для Рассмотрим два оставшихся выражения:
4. Пусть
5). Положим если использовать задачу №1. 6).
7). Положим = = 8). Введем событие
Аналогично
Замечание. Запись 9). По аналогии с задачей №8 доказывается, что последовательность
10.
11. а) Да, ибо
б) Да, ибо
в) Да, если
С другой стороны,
Если Тогда
12)
С другой стороны
13) Если Тогда
Так как
14) Если
Тогда
15) а)
б)
16) Если
17) Состояния марковской цепи: Ø, А, В, С, АВ, АС, ВС, АВС. Найдем, например, вероятности этих состояний при условии АС. Тогда Р(Ø/АС)=2/3·1/3=2/9, ибо танки А и С уничтожили друг друга; Р(А/АС)=2/3·2/3=4/9, т.е. танк А попал, а танк С промахнулся; Р(С/АС)=1/3·1/3=1/9, т.е. А промахнулся, а С попал; Р(АС/АС)=1/3·2/3=2/9, т.е. оба промахнулись; Р(АВ/АС)=Р(В/АС)=Р(ВС/АС)=Р(АВС/АС)=0 очевидно. Цепь марковская, ибо переход из одного состояния в другое зависит только от того, какие танки остались на поле боя после предыдущего залпа. 18) Состояние марковской цепи те же, что и предыдущей задаче. Найдем, например, вероятности этих состояний при условии АС. Тогда Р(С/АС)=1/3, т.е. С попал в А, а А не стреляет в С; Р(АС/АС)=2/3, т.е. С не попал в А, и А не стреляет в С; все остальные вероятности при условии АС очевидно равны нулю. 19) Если случайные величины
Следовательно, 20)
21) Обозначим через 22) Если испытуемый в первый раз нажал на кнопку, то на втором табло горела зеленая лампочка, а тогда там все время будет гореть зеленая лампочка. Поэтому искомая вероятность равна произведению вероятности того, что на первом табло зажжется зеленая лампочка, и вероятности того, что в третий раз загорится синяя лампочка, т.е. Р(З/З)·Р(С/З)=1/3·2/3=2/9. 23)
Так как
Поэтому при
Тогда
Матрица Р строится, исходя из равенства: 24) а) Если i несущественное состояние, то по определению существует состояние j, в которое с положительной вероятностью, но вернуться в состояние i можно только с нулевой вероятностью. Если j существенное, то из него с положительной вероятностью можно перейти в любое существенное состояние, и утверждение доказано. Если j несущественное, то опять найдется состояние k … и т.д. Так как цепь конечна, то обязательно на этом пути встретится существенное состояние, ибо иначе цепь вернется в какое – то несущественное состояние с положительной вероятностью, что противоречит определению.
б) От противного. Если из существенного состояния i перешли в несущественное состояние j с положительной вероятностью, то из j можно перейти в некоторое состояние k с положительной вероятностью, но вернуться назад можно только с нулевой вероятностью. Если k существенное, то k и i сообщаются и поэтому можно вернуться в состояние j с положительной вероятностью, что противоречит определению. Если же k несущественное, то найдется состояние m … и т.д. Так как цепь конечна, то приходим к противоречию. 25) От противного: пусть состояние j несущественное и возвратное. Если 26) а) Пусть б) От противного. Пусть в) Так как 27) Состояние j возвратно, если
28) Так как состояние j невозвратное, то ряд
29) См. решение задач 25 и 28. 30) Так как Если цепь непериодическая и неразложимая, то имеет место эргодическая теорема Маркова для конечной цепи, т.е. существуют пределы 31) Пусть
где
32) Так как 33) Применить критерий возвратности, заметив что 34) Пусть состояние i возвратное, но несущественное. Тогда существуют состояние j и n ≥1 такие, что Пусть теперь состояние i существенно. Если состояние i не сообщается с другими состояниями, то 35) а) Если i несущественное состояние, то существует такое состояние j, что б) Если i и j не сообщающиеся состояния, то либо 36) Так как 37) Пусть
40) Ситуация описывается марковской цепью с двумя состояниями: 1 – новость сохраняет смысл, 2 – смысл новости меняется на противоположный, причем 41) Ситуация описывается марковской цепью с тремя состояниями: А, В, С. Матрица переходов за один шаг имеет вид 42) Предсказать погоду на следующий день можно по матрице P, а на два дня по матрице P(2)=P2. Для решения вопроса об использовании монеты надо найти предельное распределение, которое существует, так как P>0, т.е. цепь регулярная, т.е. эргодическая. 43) Система образует цепь Маркова, так как вероятность попадание в данное состояние зависит – по определению – только от предшествующего состояния. Матрица переходных вероятностей P имеет вид:
Предельные вероятности находятся из системы
44) Рассмотрим марковскую цепь с двумя состояниями: (кн.1, кн. 2). Для первой тактики поведения матрица переходных вероятностей имеет вид
так как в первой книге неверна треть всех номеров, а во второй – четверть всех номеров. В этом случае стационарное распределение имеет вид (3/7,4/7), т.е. первая книга выбирается с вероятностью 3/7, вторая – 4/7. Тогда средняя доля правильных звонков равна 2/3·3/7+3/4·4/7=5/7≈0,714.
Для второй тактики поведения матрица переходных вероятностей имеет вид
так как вероятность перехода от первой книги ко второй равна (1/3)2, а от второй к первой (1/4)2. В этом случае стационарное распределение имеет вид (9/25,16/25). Тогда средняя доля правильных звонков равна 2/3·9/25+3/4·16/25=18/25=0,72. 45) 46) 47) Ситуация описывается марковской цепью, состояния которой цифры на той грани, на которой кубик лежит. Матрица переходных вероятностей за 1 шаг имеет вид:
Так как Р(2)=Р2>0, то цепь эргодическая и предельное распределение существует и находится как решение системы уравнений 48) Покажем, что
49) В силу теоремы Маркова для конечной цепи регулярность эквивалентна эргодичности цепи, а эта последняя эквивалентна для конечной цепи ее неразложимости и непериодичности. Эта цепь неразложима и периодическая с периодом d =2, т.е. не будет регулярной. 50) Марковская цепь представляет собой один класс существенных сообщающихся между собой состояний. Так как 51) Предположим, что все состояния несущественные. Если i несущественное состояние, то найдется состояние k, в которое можно перейти с положительной вероятностью, а назад вернуться нельзя. Так как k несущественное, то найдется состояние m и т.д. Но цепь конечная, а потому обязательно будет возврат в какое-то несущественное состояние с положительной вероятностью, что противоречит определению несущественного состояния. 52)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.172.68 (0.103 с.) |
 через условные вероятности события А.
через условные вероятности события А.
 для полной системы событий
для полной системы событий  ?
?
 – случайный вектор. Опишите все события s–алгебры F x.
– случайный вектор. Опишите все события s–алгебры F x.
 – случайная величина, принимающая только значения 1, 2 и 3. Опишите все события s–алгебры F x.
– случайная величина, принимающая только значения 1, 2 и 3. Опишите все события s–алгебры F x.
 , то случайная величина x постоянна на каждом событии этой системы.
, то случайная величина x постоянна на каждом событии этой системы.
 как функция А Î F при В Î F, Р(В) ¹ 0 будет вероятностной мерой на F.
как функция А Î F при В Î F, Р(В) ¹ 0 будет вероятностной мерой на F.
 .
.
 является некоторой борелевской функцией
является некоторой борелевской функцией  от случайной величины
от случайной величины  п.н.. Доказать.
п.н.. Доказать.
 , если W = [0;1], Р – лебегова мера,
, если W = [0;1], Р – лебегова мера,  ,
, 
 .
.
 ,
,  .
.
 :
:  и
и  в противном случае.
в противном случае.
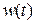 винеровский процесс, то
винеровский процесс, то  также винеровский процесс.
также винеровский процесс.
 винеровский процесс, то
винеровский процесс, то  также винеровский процесс.
также винеровский процесс.
 .
.
 .
.
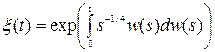 .
.
 ;
б).
;
б).  ;
в).
;
в).  ;
г).
;
г).  ;
д).
;
д).  ;
е).
;
е).  ;
ж).
;
ж).  ;
з).
;
з). 
 .
.
 .
.
 .
.
 ,
,  .
.
 ,
,  .
.
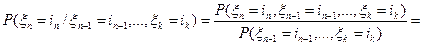

 ;
;
 ; с другой стороны,
; с другой стороны, ;
;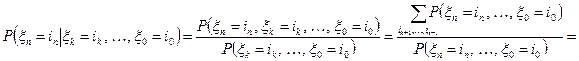
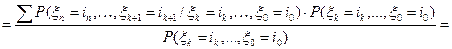
 в силу равенства б).
в силу равенства б).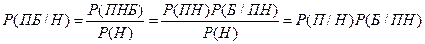 . Покажем, что
. Покажем, что  :
: 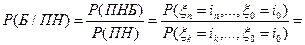
 .
. ;
;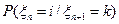 .
.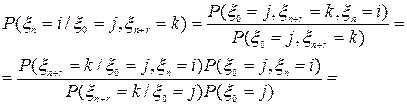
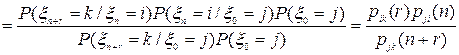 и
и
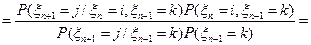
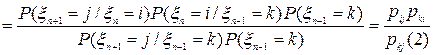 в силу задачи 1.
в силу задачи 1. ,
,  , подпоследовательность последовательности
, подпоследовательность последовательности 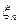 ,
,  . Тогда
. Тогда
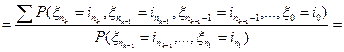
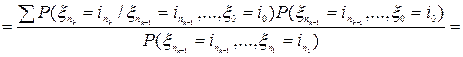
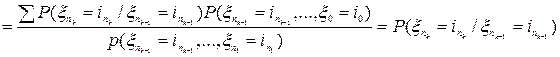 , где сумма берется по всем попущенным индексам от 0 до
, где сумма берется по всем попущенным индексам от 0 до 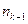 и используется задача 1.
и используется задача 1. . Тогда
. Тогда 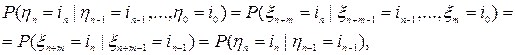
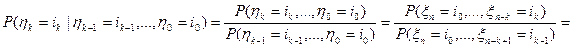

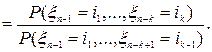 Повторяя этот прием, приходим к выражению
Повторяя этот прием, приходим к выражению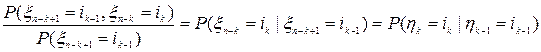 .
.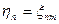 . Тогда
. Тогда  =
= 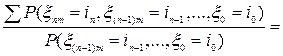

 , где сумма берется по всем пропущенным номерам от нуля до (n -1) m и используется задача №1.
, где сумма берется по всем пропущенным номерам от нуля до (n -1) m и используется задача №1.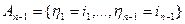 , состоящее в том, что случайные величины
, состоящее в том, что случайные величины 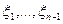 могут принимать значения из множества
могут принимать значения из множества  в зависимости от значений случайных величин
в зависимости от значений случайных величин 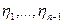 . Тогда
. Тогда 
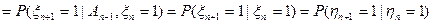 в силу того, что исходная цепь марковская.
в силу того, что исходная цепь марковская.
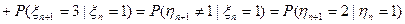 ,
,
 , так же вычисляется
, так же вычисляется Следовательно, последовательность
Следовательно, последовательность  является цепью Маркова. Найдем матрицу
является цепью Маркова. Найдем матрицу  вероятностей перехода за 1 шаг:
вероятностей перехода за 1 шаг: 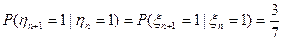 , тогда
, тогда  ;
;
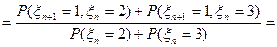
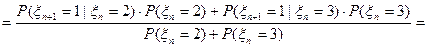
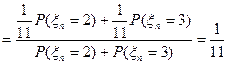 , а тогда
, а тогда 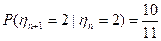 .
. , означает, что - либо
, означает, что - либо  , либо
, либо  .
.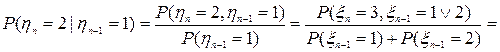
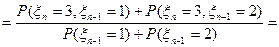
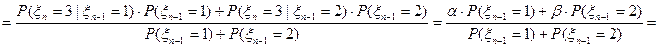
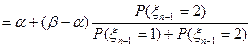 , для однородной цепи это выражение не зависит от
, для однородной цепи это выражение не зависит от  , поэтому
, поэтому  ,
,  .
.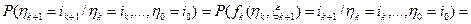
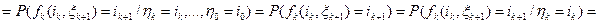
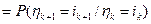 в силу независимости случайной величины
в силу независимости случайной величины  от случайных величин
от случайных величин 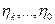 .
.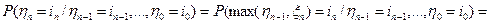
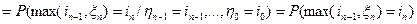 в силу независимости случайных величин
в силу независимости случайных величин 
 по той же причине.
по той же причине.
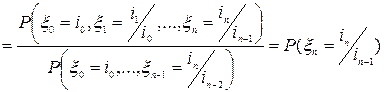 в силу независимости случайных величин
в силу независимости случайных величин 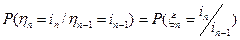 .
. , нет – при
, нет – при 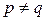 . Действительно, при
. Действительно, при  :
: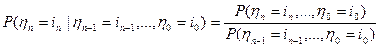 , но
, но 
 где
где 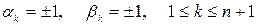 и аналогично
и аналогично 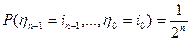 , т.е.
, т.е.  .
.
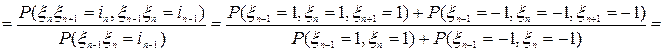
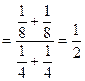 в силу независимости случайных величин
в силу независимости случайных величин  ,
,  .
.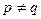 , то положим, например,
, то положим, например,  .
.
 , но
, но
 .
.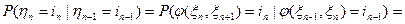
 .
.
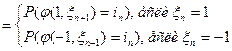 , в силу независимости случайных величин
, в силу независимости случайных величин  , таким образом последовательность
, таким образом последовательность  , образует марковскую цепь. Найдем матрицу P переходных вероятностей за 1 шаг:
, образует марковскую цепь. Найдем матрицу P переходных вероятностей за 1 шаг:
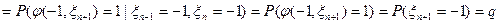 ,
,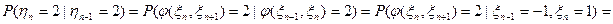
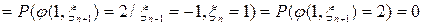 и так далее.
и так далее.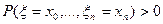 , то
, то  .
.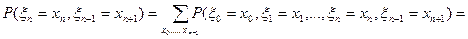

 .
. по условию, то
по условию, то 
 и поэтому цепь марковская.
и поэтому цепь марковская.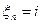 , то в момент
, то в момент  длина очереди равна
длина очереди равна  , где
, где , то есть
, то есть  , где
, где  .
.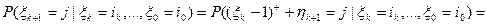
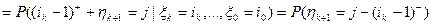 в силу независимости случайных величин
в силу независимости случайных величин  . Аналогично вычисляем
. Аналогично вычисляем  .
. , где либо
, где либо  , либо
, либо  и случайные величины
и случайные величины 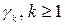 , независимы. Тогда
, независимы. Тогда  и
и 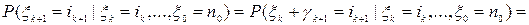
 в силу независимости случайных величин
в силу независимости случайных величин 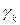 . Аналогично вычисляем
. Аналогично вычисляем  .
.
 , где
, где 
 . Аналогично вычисляется
. Аналогично вычисляется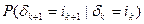 .
. то
то 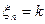 , если в момент n или ранее он закончил проверку дефектного изделия. Тогда
, если в момент n или ранее он закончил проверку дефектного изделия. Тогда  равно 0 или 1 соответственно, то есть зависит от предыстории процесса.
равно 0 или 1 соответственно, то есть зависит от предыстории процесса. , т.е. строки одинаковы. Пусть строки одинаковы, т.е.
, т.е. строки одинаковы. Пусть строки одинаковы, т.е. 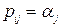 ,
,  . Тогда
. Тогда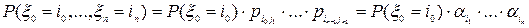 и
и 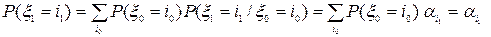 ,
,  и далее по аналогии
и далее по аналогии 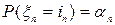 .
. , т.е. случайные величины
, т.е. случайные величины  в силу независимости случайных величин
в силу независимости случайных величин  при
при 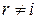 . С другой стороны
. С другой стороны 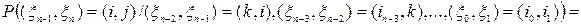
 в силу независимости случайных величин
в силу независимости случайных величин  и
и  ; очевидно, что
; очевидно, что 
 в силу независимости случайных величин
в силу независимости случайных величин 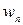 ,
,  , т.е. цепь марковская. В силу того, что случайные величины
, т.е. цепь марковская. В силу того, что случайные величины  , то
, то  и
и
 . В силу независимости случайных величин
. В силу независимости случайных величин 


 .
.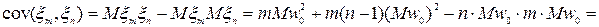
 .
.
 .
. вероятность когда-нибудь вернуться в состояние j, выйдя из него, то
вероятность когда-нибудь вернуться в состояние j, выйдя из него, то  -вероятность никогда в него не вернуться, выйдя из него. По определению несущественного состояния существует целое
-вероятность никогда в него не вернуться, выйдя из него. По определению несущественного состояния существует целое  и для любого
и для любого 
 . Тогда
. Тогда  , но для возвратного состояния
, но для возвратного состояния  , т.е. получили противоречие.
, т.е. получили противоречие. ,
, 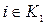 ,
,  . Тогда существуют
. Тогда существуют  ,
,  такие, что
такие, что  и
и  , откуда
, откуда  . Аналогично покажем, что существует
. Аналогично покажем, что существует  . Следовательно,
. Следовательно,  и
и  , т.е.
, т.е.  и
и  .
. ,
,  и существуют
и существуют  , т.е.
, т.е.  , и
, и  , т.е.
, т.е.  . Так как
. Так как  такие, что
такие, что  и
и  . Тогда
. Тогда  . Аналогично покажем, что существует такое k, что
. Аналогично покажем, что существует такое k, что  . Следовательно,
. Следовательно,  и
и  принадлежат одному классу, т.е.
принадлежат одному классу, т.е.  и
и  совпадают.
совпадают. ; аналогично
; аналогично  влечет существование
влечет существование  ,
,  ,
,  . Но
. Но  такое, что
такое, что  . Тогда
. Тогда  , т.е.
, т.е.  .
. и
и  - вероятность первого попадания в состояние j за n шагов, выйдя из него. Так как цепь состоит из существенных сообщающихся между собой состояний, то для доказательства возвратности можно выбрать любое состояние. Положим j =0. Тогда
- вероятность первого попадания в состояние j за n шагов, выйдя из него. Так как цепь состоит из существенных сообщающихся между собой состояний, то для доказательства возвратности можно выбрать любое состояние. Положим j =0. Тогда 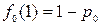 ,
,  ,
, 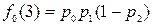 ,…,
,…,  и т.д. Найдем
и т.д. Найдем 
 . Следовательно,
. Следовательно,  сходится к нулю, критерием чего является сходимость ряда
сходится к нулю, критерием чего является сходимость ряда  и условие
и условие  ,
,  .
. сходящийся, т.е.
сходящийся, т.е. 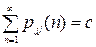 . Очевидно, что
. Очевидно, что . Тогда
. Тогда

 , то из
, то из  следует
следует  ; если бы цепь была периодической с периодом d, то d/n и d/n+ 1, т.е. d =1, и получили противоречие (
; если бы цепь была периодической с периодом d, то d/n и d/n+ 1, т.е. d =1, и получили противоречие ( для любых состояний i и k. В силу конечности цепи найдется такое n, что
для любых состояний i и k. В силу конечности цепи найдется такое n, что  для любых состояний i и k.
для любых состояний i и k.
 ,
,  , марковская цепь. Тогда
, марковская цепь. Тогда  есть число возвращений в состояние j, выйдя из него. Среднее число возвращений равно
есть число возвращений в состояние j, выйдя из него. Среднее число возвращений равно , а эта сумма – в силу критерия возвратности состояния – либо конечна, либо нет для всех состояний неразложимой цепи.
, а эта сумма – в силу критерия возвратности состояния – либо конечна, либо нет для всех состояний неразложимой цепи. , то существует состояние j такое, что
, то существует состояние j такое, что  не стремится к нулю при
не стремится к нулю при  . Если бы все состояния были невозвратными, то для любого состояния i в силу задачи 28
. Если бы все состояния были невозвратными, то для любого состояния i в силу задачи 28  при
при  .
. и
и  для любого k ≥1. Обозначим через
для любого k ≥1. Обозначим через  вероятность события «вернуться в состояние i когда-нибудь, выйдя из него». Тогда это событие влечет событие А={цепь не попадает в состояние j, выйди из состояния i }, так как
вероятность события «вернуться в состояние i когда-нибудь, выйдя из него». Тогда это событие влечет событие А={цепь не попадает в состояние j, выйди из состояния i }, так как  , что приводит к противоречию, ибо
, что приводит к противоречию, ибо  для возвратного состояния.
для возвратного состояния. для всех n ≥1, т.е. i возвратное. Если состояние i сообщается с другими состояниями, то в силу задачи 32 одно из них возвратное, а следовательно все возвратные.
для всех n ≥1, т.е. i возвратное. Если состояние i сообщается с другими состояниями, то в силу задачи 32 одно из них возвратное, а следовательно все возвратные. для любого n ≥1, т.е.
для любого n ≥1, т.е.  .
. , либо
, либо  , либо
, либо  стремится к
стремится к  при
при  , в силу эргодичности, то
, в силу эргодичности, то  стремится к величине
стремится к величине  при
при  в силу эргодической теоремы.
в силу эргодической теоремы. вероятность, выйдя из состояния i, вернуться в него впервые на n -м шаге, тогда
вероятность, выйдя из состояния i, вернуться в него впервые на n -м шаге, тогда  вероятность когда-нибудь вернуться в состояние i, выйдя из него. Если
вероятность когда-нибудь вернуться в состояние i, выйдя из него. Если  вероятность, выйдя из состояния i, возвращаться в него, по крайней мере N раз, то по ФПВ
вероятность, выйдя из состояния i, возвращаться в него, по крайней мере N раз, то по ФПВ . Тогда
. Тогда  - вероятность, выйдя из состояния i, возвращаться в него бесконечное число раз, равна
- вероятность, выйдя из состояния i, возвращаться в него бесконечное число раз, равна  , т.е. равна 1, если
, т.е. равна 1, если  (состояние i невозвратно).
(состояние i невозвратно). . Система уравнений для предельных вероятностей имеет вид:
. Система уравнений для предельных вероятностей имеет вид: 
 . Так как Р2>0, то цепь регулярная, т.е. существуют предельные вероятности. Для их описания составляется система уравнений:
. Так как Р2>0, то цепь регулярная, т.е. существуют предельные вероятности. Для их описания составляется система уравнений: 


 .
. ,
,  .
. . Введем события
. Введем события ,
, ,
, . Очевидно, что
. Очевидно, что  и
и  . Тогда
. Тогда 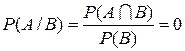 и
и  .
. .
. , то состояние 1 непериодическое, а поэтому все непериодические. Так как вероятность вернуться в состояние 1 впервые, выйдя из него на 1-м, 2-м, …, n -м шаге, равны соответственно
, то состояние 1 непериодическое, а поэтому все непериодические. Так как вероятность вернуться в состояние 1 впервые, выйдя из него на 1-м, 2-м, …, n -м шаге, равны соответственно  ,
,  ,…,
,…, 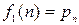 и
и  при
при 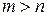 , то
, то  , т.е. состояние 1 возвратно, а потому все возвратные. Цепь регулярная, так как Р(n)=Р n >0, а следовательно эргодическая, и поэтому предельное распределение существует и находится из системы уравнений
, т.е. состояние 1 возвратно, а потому все возвратные. Цепь регулярная, так как Р(n)=Р n >0, а следовательно эргодическая, и поэтому предельное распределение существует и находится из системы уравнений 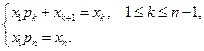

 в силу независимости случайных величин
в силу независимости случайных величин  .
.


