
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в теорию случайных процессовСтр 1 из 3Следующая ⇒
Оглавление Предисловие. 3 1. Введение в теорию случайных процессов. 4 2. Дискретные марковские цепи. 6 3. Корреляционная теория случайных процессов. 16 4. Условные математические ожидания. 20 5. Винеровский процесс и интегралы Ито. 21 Решения 2. Дискретные марковские цепи. 23 4. Условные математические ожидания. 40 5. Винеровский процесс и интеграл Ито. 43 Ответы (Дискретные марковские цепи) 45
Предлагаемый сборник задач предназначен для использования на семинарских занятиях по курсу «Теория случайных процессов» для студентов механико-математического факультета. Его цель – помочь студентам, овладевшим основами теории вероятностей, познакомиться с основными понятиями теории случайных процессов и овладеть методами решения задач, связанных с дискретными цепями Маркова, корреляционной теорией случайных процессов, винеровским процессом, интегралом Ито и стохастическими дифференциальными уравнениями. Отдельный раздел посвящен очень интересной теме – условные математические ожидания относительно σ – алгебры. Для части задач приведены решения. При составлении сборника использовались и известные задачи, возникшие в результате педагогической деятельности авторов. Авторы будут благодарны за любые замечания, способствующие улучшению данного пособия. Дискретные марковские цепи. Задачи. 1. Пусть последовательность случайных величин а) б) в) 2. Пусть последовательность случайных величин 3. Пусть последовательность случайных величин 4. Пусть последовательность случайных величин 5. Если 6. Пусть случайные величины 7. Если
8. Пусть 9. Пусть последовательность случайных величин 10. Пусть 11. Пусть 12. Пусть 13. Пусть
14. На стоянку такси через единичные моменты времени прибывают машины (по одной в каждый момент). Если на стоянке нет ожидающих, то машина сразу уезжает. Обозначим через 15. В начальный момент в урне
а) б) 16. К рабочему, стоящему на контроле, через минуту поступают изделия, причём каждое из них независимо от других может оказаться дефектным с вероятностью p, 0<p<1. Поступившие изделия рабочий одно за другим проверяет, затрачивая на проверку каждого по одной минуте. Если изделие оказывается дефектным, то он прекращает проверку других изделий и исправляет дефектное, на что уходит ещё 5 минут. Пусть 17. Три танка ведут бой, каждый с двумя другими. Танк A уничтожает танк, по которому он ведёт огонь, с вероятностью 2/3, танк B – с вероятностью 1/2, танк C – с вероятностью 1/3. Танки открывают огонь одновременно, и каждый стреляет по сильнейшему из не уничтоженных к этому моменту противников. Написать матрицу вероятностей перехода за один шаг марковской цепи, состояниями которой будут множества танков, которые еще действуют в данный момент. 18. Три танка ведут бой, танк А стреляет в танк В, танк В – в танк С, танк С – в танк А. Танк А уничтожает танк В с вероятностью 2/3, танк В уничтожает танк С с вероятностью 1/2, танк С уничтожает танк А с вероятностью 1/3. Танки открывают огонь одновременно. Написать матрицу вероятностей перехода за один шаг марковской цепи, состояниями которой будут множества танков, которые еще действуют в данный момент. 19. Пусть последовательность случайных величин 20. Пусть 21. Эскадрилья бомбардировщиков состоит из четырех самолетов. Боевое задание она получает один раз в день. Если к концу дня из-за потерь, нанесенных противником, наличный состав самолетов уменьшается до нуля, одного или двух, то командир эскадрильи получает один самолет из резерва; этот самолет доставляется ночью. Если наличный состав равен трем или четырем самолетам, то командир не имеет права на пополнение. На следующий день, если в наличии имеется три или четыре самолета, то задание эскадрилье дается; в противном случае задание отменяется. Во время выполнения задания каждый самолет может быть выведен из строя с вероятностью р. Ввести понятие состояния эскадрильи так, чтобы функционирование эскадрильи можно было описать с помощью цепи Маркова, построить матрицу Р и исследовать ее на регулярность. 22. Перед испытуемым находятся два табло с синими и зелеными лампочками. Последовательности зажигания описываются Марковскими цепями с матрицами перехода за один шаг 1) Испытуемый должен нажать на кнопку, если на обоих табло зажегся зеленый свет. С какой вероятностью после двух правильных нажатий подряд он может ожидать ситуацию, когда не надо нажимать? 23. Пусть
24. Для конечной цепи Маркова, состоящей из одного класса несущественных состояний и одного класса существенных состояний, доказать, что: а) из несущественного состояния можно перейти в любое существенное с положительной вероятностью; б) из существенного состояния нельзя перейти в несущественное с положительной вероятностью. 25. Доказать, что несущественное состояние не может быть возвратным. 26. Два состояния i и j марковской цепи отнесем к одному классу K, если существуют такие целые а) различные классы не пересекаются; б) если в) если 27. Состояния цепи Маркова - неотрицательные целые числа. Из состояния j, 28. Доказать, что если j невозвратное состояние, то для любого состояния i марковской цепи 29. Доказать, что если состояние j несущественное, то 30. Доказать, что конечная неразложимая цепь Маркова является непериодической тогда и только тогда, когда существует целое 31. Доказать, что для неразложимой цепи Маркова среднее число возвращений в данное состояние, выйдя из него, либо конечно для всех состояний, либо бесконечно для всех состояний. 32. Доказать, что любая цепь Маркова с конечным числом состояний имеет по крайней мере одно возвратное состояние. 33. Пусть все состояния двух цепей Маркова с матрицами вероятностей перехода за один шаг 34. Доказать, что в конечной цепи Маркова состояние возвратно тогда и только тогда, когда оно существенно. 35. Доказать, что цепь Маркова не является эргодической, если: а) в ней имеется по крайней мере одно несущественное состояние; б) в ней имеется по крайней мере два не сообщающихся состояния. 36. Пусть последовательность целочисленных случайных величин
37. Доказать, что для любого состояния цепи Маркова вероятность возвращения в него бесконечное число раз равна 0 или 1, причем в первом случае состояние невозвратно, а во втором возвратно.
38. По виду матрицы переходных вероятностей за один шаг: 1) восстановить недостающие вероятности; 2) построить граф переходов; 3) выделить классы несущественных и существенных состояний; 4) выяснить, является ли марковская цепь эргодической, и найти предельные вероятности; 5) Задав начальное распределение, найти вероятность за три шага попасть в третье состояние: а) г) з) к) м) п) 39. Дать классификацию состояний марковской цепи, найти предельные вероятности, если переходные матрицы за один шаг имеют вид: а) в) д) 40. Пусть каждый человек, услышавший новость, может передать ее другому; при этом вероятность искажения смысла на противоположный постоянна и равна р =0,00001. Какова вероятность услышать новость в неискаженном виде после того, как она «побывала» у большого числа людей? 41. Известно, что если погоду в данной местности характеризовать только следующими состояниями: облачно, дождь и хорошая погода, то запись текущей погоды образует марковскую цепь с матрицей вероятностей перехода 43. 44. Вернувшись после долгого отсутствия в родной город, вы решили позвонить по телефону всем вашим старым друзьям и сообщить о своем приезде. Под руками у вас оказались две устаревшие телефонные книги, причем вас предупредили, что в одной из них неверно уже около трети всех номеров, а в другой – около четверти, но, в какой именно, неизвестно. Можно избрать две такие тактики поведения: 1) книга выбирается наугад и, если указанный в ней номер нужного вам телефона оказался правильным, вы продолжаете ею пользоваться, если нет – берете другую книгу; 2) метод двух проб: в случаях «правильный – правильный», «правильный – неправильный» и «неправильный – правильный» книга не меняется, в случае «неправильный – неправильный» надо перейти к другой книге. При какой тактике поведения вероятность правильных телефонных показателей выше? 47. Игральная кость последовательно перекладывается с одной грани равновероятно на любую из четырех соседних независимо от предыдущего. К какому пределу при 48. 49. На окружности расположены шесть точек, равноудаленных друг от друга. Частица из данной точки перемещается в одну из ближайших соседних с вероятностью ¼ или в диаметрально противоположную с вероятностью ½. Построить граф, написать матрицу вероятностей переходов за один шаг. Будет ли эта марковская цепь регулярной?
50. Пусть 51. Доказать, что все состояния конечной цепи Маркова не могут быть несущественными. 52. Пусть Решения. Дискретные марковские цепи. 1. а)
б)
в)
2.
3. P( аналогично для Рассмотрим два оставшихся выражения:
4. Пусть
5). Положим если использовать задачу №1. 6).
7). Положим = = 8). Введем событие
Аналогично
Замечание. Запись 9). По аналогии с задачей №8 доказывается, что последовательность
10.
11. а) Да, ибо
б) Да, ибо
в) Да, если
С другой стороны,
Если Тогда
12)
С другой стороны
13) Если Тогда
Так как
14) Если
Тогда
15) а)
б)
16) Если 17) Состояния марковской цепи: Ø, А, В, С, АВ, АС, ВС, АВС. Найдем, например, вероятности этих состояний при условии АС. Тогда Р(Ø/АС)=2/3·1/3=2/9, ибо танки А и С уничтожили друг друга; Р(А/АС)=2/3·2/3=4/9, т.е. танк А попал, а танк С промахнулся; Р(С/АС)=1/3·1/3=1/9, т.е. А промахнулся, а С попал; Р(АС/АС)=1/3·2/3=2/9, т.е. оба промахнулись; Р(АВ/АС)=Р(В/АС)=Р(ВС/АС)=Р(АВС/АС)=0 очевидно. Цепь марковская, ибо переход из одного состояния в другое зависит только от того, какие танки остались на поле боя после предыдущего залпа. 18) Состояние марковской цепи те же, что и предыдущей задаче. Найдем, например, вероятности этих состояний при условии АС. Тогда Р(С/АС)=1/3, т.е. С попал в А, а А не стреляет в С; Р(АС/АС)=2/3, т.е. С не попал в А, и А не стреляет в С; все остальные вероятности при условии АС очевидно равны нулю. 19) Если случайные величины
Следовательно, 20)
21) Обозначим через
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.151 с.) |
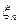 ,
,  , образует цепь Маркова. Доказать, что для
, образует цепь Маркова. Доказать, что для  :
: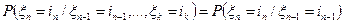 ;
;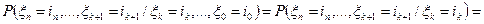
 ;
;
 ,
,  , образует цепь Маркова. Положим П
, образует цепь Маркова. Положим П  т.е. «прошлое»
т.е. «прошлое»  т.е. «настоящее»/ и
т.е. «настоящее»/ и 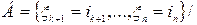 т.е. «будущее»/. Доказать, что Р(ПБ/Н)=Р(П/Н)*Р(Б/Н).
т.е. «будущее»/. Доказать, что Р(ПБ/Н)=Р(П/Н)*Р(Б/Н).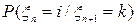 ,
, 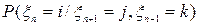 ,
,  и
и 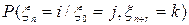 .
. ,
,  натуральное, тоже образует цепь Маркова. Доказать.
натуральное, тоже образует цепь Маркова. Доказать. образуют цепь Маркова. Доказать, что случайные величины
образуют цепь Маркова. Доказать, что случайные величины 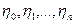 , где
, где 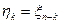 ,
,  , также образует цепь Маркова.
, также образует цепь Маркова. ,
,  , матрица вероятностей перехода равна
, матрица вероятностей перехода равна 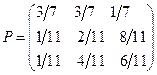 и начальное распределение
и начальное распределение 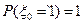 . Положим
. Положим  Доказать, что последовательность
Доказать, что последовательность  ,
, 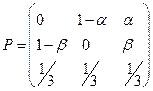 и множеством состояний {1,2,3}. Положим
и множеством состояний {1,2,3}. Положим 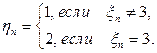 При каком условии последовательность случайных величин
При каком условии последовательность случайных величин  - некоторые измеримые функции. Доказать, что последовательность случайных величин
- некоторые измеримые функции. Доказать, что последовательность случайных величин  , где
, где 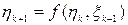 ,
, 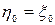 образует цепь Маркова.
образует цепь Маркова.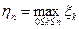 ,
, 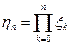 ,
, 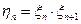 ,
,  ,
,  выполняется соотношение
выполняется соотношение , то последовательность случайных величин
, то последовательность случайных величин 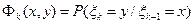 для любых
для любых  . Доказать.
. Доказать. число пассажиров, приходящих в момент k на стоянку, и будем считать, что
число пассажиров, приходящих в момент k на стоянку, и будем считать, что  - независимые случайные величины. Пусть
- независимые случайные величины. Пусть  длина очереди в момент времени k,
длина очереди в момент времени k, 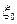 =0. Будет ли последовательность случайных величин
=0. Будет ли последовательность случайных величин 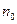 белых и
белых и 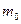 черных шаров. Через каждую единицу времени из урны (без возвращения) извлекается один шар. Пусть
черных шаров. Через каждую единицу времени из урны (без возвращения) извлекается один шар. Пусть 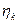 – число чёрных шаров в урне в момент времени k. Какие из указанных ниже последовательностей образуют цепь Маркова:
– число чёрных шаров в урне в момент времени k. Какие из указанных ниже последовательностей образуют цепь Маркова: ;
; ,
,  , цепью Маркова?
, цепью Маркова?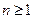 , последовательность независимых одинаково распределенных случайных величин, принимающих значения 1 и 0 с вероятностями p и q=1-p соответственно. Доказать, что последовательность пар
, последовательность независимых одинаково распределенных случайных величин, принимающих значения 1 и 0 с вероятностями p и q=1-p соответственно. Доказать, что последовательность пар 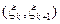 ,
,  , образует цепь Маркова и найти матрицу Р вероятностей перехода за один шаг.
, образует цепь Маркова и найти матрицу Р вероятностей перехода за один шаг. 2)
2) 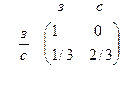 .
.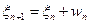 ,
, 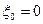 , где
, где  ,
,  ,
,  и
и  , построить матрицу переходных вероятностей за один шаг, если случайные величины
, построить матрицу переходных вероятностей за один шаг, если случайные величины 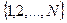 .
. ,
, 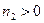 , что
, что  . Введем на множестве классов состояний отношение «<»: будем говорить, что
. Введем на множестве классов состояний отношение «<»: будем говорить, что 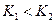 , если существуют состояния
, если существуют состояния  и
и 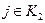 целое
целое  такие, что
такие, что  . Доказать, что:
. Доказать, что: ;
;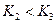 , то
, то 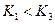 .
.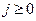 , за один шаг цепь переходит в состояние j+1 с вероятностью
, за один шаг цепь переходит в состояние j+1 с вероятностью  и в состояние ноль с вероятностью 1-
и в состояние ноль с вероятностью 1- 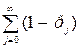 расходился и
расходился и 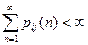 .
.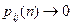 для любого состояния i при
для любого состояния i при 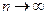 .
. для любых состояний i и k.
для любых состояний i и k.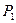 и
и  возвратны. Будут ли возвратны состояния цепи Маркова с матрицей вероятностей перехода за один шаг
возвратны. Будут ли возвратны состояния цепи Маркова с матрицей вероятностей перехода за один шаг 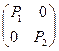 ?
? ,
, 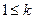 ,
,  . Доказать, что существует
. Доказать, что существует  и
и 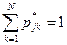 для всех j,
для всех j,  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е) 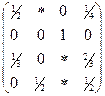 ; ж)
; ж)  ;
; ; и)
; и)  ;
;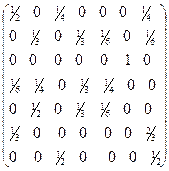 ; л)
; л) 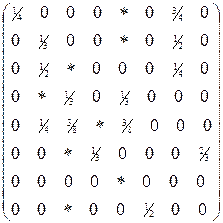 ;
;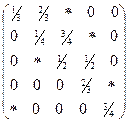 ; н)
; н) 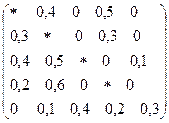 ; о)
; о)  ;
; ; р)
; р) 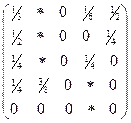 ; с)
; с) 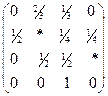 .
.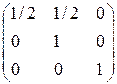 ; б)
; б)  ;
;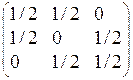 ; г)
; г)  ;
; ; ж)
; ж) 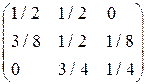 .
. . Предскажите погоду на один и на два дня вперед, если сегодня погода дождливая.
. Предскажите погоду на один и на два дня вперед, если сегодня погода дождливая.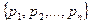 первая строка стохастической матрицы Р;
первая строка стохастической матрицы Р;  >0,
>0, 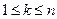 . В следующих строках
. В следующих строках 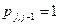 , остальные элементы матрицы равны нулю. Классифицировать состояния марковской цепи и найти предельное распределение.
, остальные элементы матрицы равны нулю. Классифицировать состояния марковской цепи и найти предельное распределение.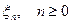 , последовательность независимых целочисленных случайных величин и d>0 целое число. Доказать, что случайные величины
, последовательность независимых целочисленных случайных величин и d>0 целое число. Доказать, что случайные величины  ,
, 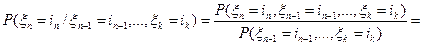

 ;
;
 ; с другой стороны,
; с другой стороны, ;
;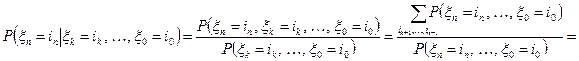
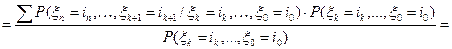
 в силу равенства б).
в силу равенства б).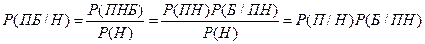 . Покажем, что
. Покажем, что  :
: 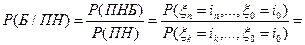
 .
. ;
;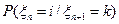 .
.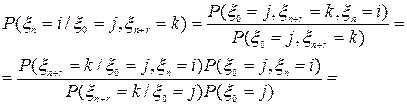
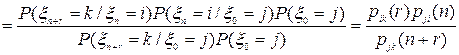 и
и
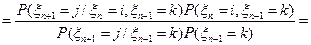
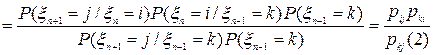 в силу задачи 1.
в силу задачи 1. ,
, 
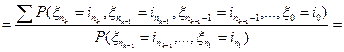
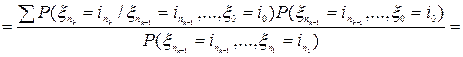
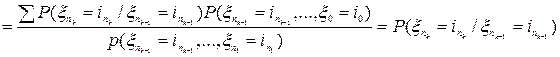 , где сумма берется по всем попущенным индексам от 0 до
, где сумма берется по всем попущенным индексам от 0 до 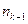 и используется задача 1.
и используется задача 1. . Тогда
. Тогда 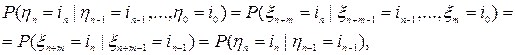
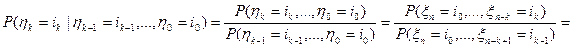

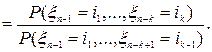 Повторяя этот прием, приходим к выражению
Повторяя этот прием, приходим к выражению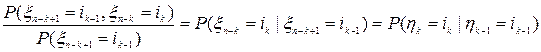 .
.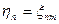 . Тогда
. Тогда  =
= 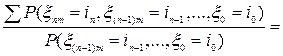

 , где сумма берется по всем пропущенным номерам от нуля до (n -1) m и используется задача №1.
, где сумма берется по всем пропущенным номерам от нуля до (n -1) m и используется задача №1.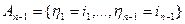 , состоящее в том, что случайные величины
, состоящее в том, что случайные величины 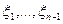 могут принимать значения из множества
могут принимать значения из множества  в зависимости от значений случайных величин
в зависимости от значений случайных величин 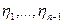 . Тогда
. Тогда 
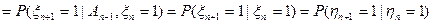 в силу того, что исходная цепь марковская.
в силу того, что исходная цепь марковская.
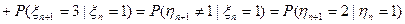 ,
,
 , так же вычисляется
, так же вычисляется Следовательно, последовательность
Следовательно, последовательность  является цепью Маркова. Найдем матрицу
является цепью Маркова. Найдем матрицу  вероятностей перехода за 1 шаг:
вероятностей перехода за 1 шаг: 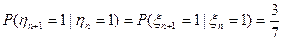 , тогда
, тогда  ;
;
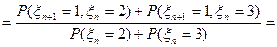
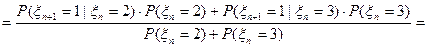
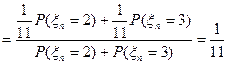 , а тогда
, а тогда 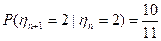 .
. , означает, что - либо
, означает, что - либо  , либо
, либо  .
.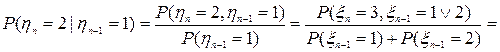
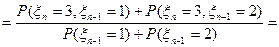
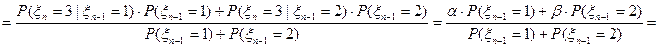
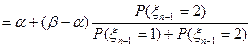 , для однородной цепи это выражение не зависит от
, для однородной цепи это выражение не зависит от  ,
,  .
.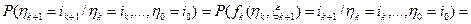
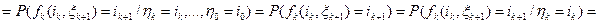
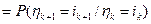 в силу независимости случайной величины
в силу независимости случайной величины  от случайных величин
от случайных величин 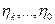 .
.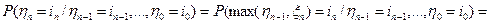
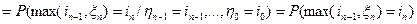 в силу независимости случайных величин
в силу независимости случайных величин 
 по той же причине.
по той же причине.
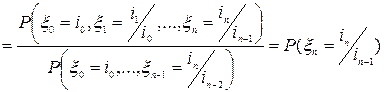 в силу независимости случайных величин
в силу независимости случайных величин 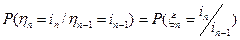 .
. , нет – при
, нет – при 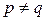 . Действительно, при
. Действительно, при  :
: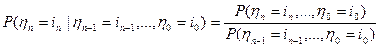 , но
, но 
 где
где 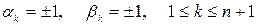 и аналогично
и аналогично 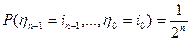 , т.е.
, т.е.  .
.
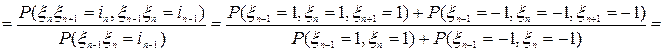
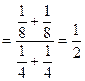 в силу независимости случайных величин
в силу независимости случайных величин 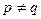 , то положим, например,
, то положим, например,  .
.
 , но
, но
 .
.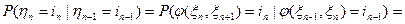
 .
.
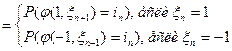 , в силу независимости случайных величин
, в силу независимости случайных величин  , таким образом последовательность
, таким образом последовательность  , образует марковскую цепь. Найдем матрицу P переходных вероятностей за 1 шаг:
, образует марковскую цепь. Найдем матрицу P переходных вероятностей за 1 шаг:
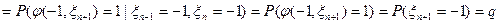 ,
,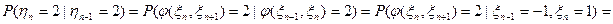
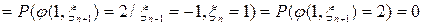 и так далее.
и так далее.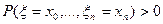 , то
, то  .
.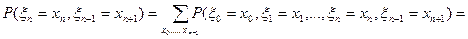

 .
. по условию, то
по условию, то 
 и поэтому цепь марковская.
и поэтому цепь марковская.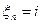 , то в момент
, то в момент  длина очереди равна
длина очереди равна  , где
, где , то есть
, то есть  , где
, где  .
.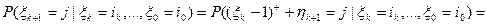
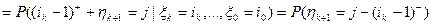 в силу независимости случайных величин
в силу независимости случайных величин  . Аналогично вычисляем
. Аналогично вычисляем  .
. , где либо
, где либо  , либо
, либо  и случайные величины
и случайные величины 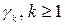 , независимы. Тогда
, независимы. Тогда  и
и 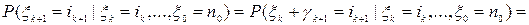
 в силу независимости случайных величин
в силу независимости случайных величин 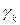 . Аналогично вычисляем
. Аналогично вычисляем  .
.
 , где
, где 
 . Аналогично вычисляется
. Аналогично вычисляется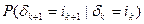 .
. то
то 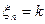 , если в момент n или ранее он закончил проверку дефектного изделия. Тогда
, если в момент n или ранее он закончил проверку дефектного изделия. Тогда  равно 0 или 1 соответственно, то есть зависит от предыстории процесса.
равно 0 или 1 соответственно, то есть зависит от предыстории процесса. , т.е. строки одинаковы. Пусть строки одинаковы, т.е.
, т.е. строки одинаковы. Пусть строки одинаковы, т.е. 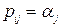 ,
,  . Тогда
. Тогда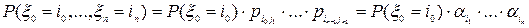 и
и 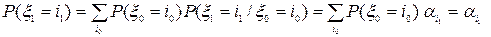 ,
,  и далее по аналогии
и далее по аналогии 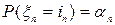 .
. , т.е. случайные величины
, т.е. случайные величины  в силу независимости случайных величин
в силу независимости случайных величин  при
при 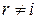 . С другой стороны
. С другой стороны 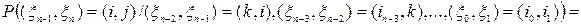
 в силу независимости случайных величин
в силу независимости случайных величин  и
и 


