
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Джерела похибки. Наближені числа. Абсолютна і відносна похибки наближеного числа.
На практиці в більшості випадків знайти точне рішення математичної задачі неможливо, тому що воно не виражається в елементарних функціях. Тому для відшукання рішення використовуються чисельні методи. Рішення, одержане чисельним методом, звичайно є наближеним, тобто містить деяку похибку. Джерелами похибки можуть бути: 1) невідповідність математичної моделі досліджуваному реальному процесу; 2) похибку вихідних даних; 3) похибку методу, що використовується; 4) похибку округлення. Оцінити похибку математичної моделі можна шляхом порівняння результатів експерименту і типових приватних рішень при фіксованих значеннях вхідних параметрів. Вплив похибки вихідних даних оцінюється шляхом варіювання вхідних перемінних у припустимих межах і фіксування результатів. Похибку методу виявляється при використанні наближених методів, в основі яких використовуються нескінченні процеси, що приводять у межі до точного рішення. Тому що число операцій обмежується, те отримане рішення є наближеним. При використанні комп'ютерів похибку округлення незначна, але при ручних розрахунках з великою кількістю операцій вона істотно може вплинути на похибку рішення. Виз. Нехай Виз. Величина Можна записати: Виз. Будь-яке число Правило 1. При складанні і відрахуванні наближених чисел, їх граничні відносні похибки складаються.
Правило 2. При множенні і розподілі складаються граничні відносні похибки наближених чисел.
Наближені методи рішення нелінійних рівнянь. Постановка задачі. Нехай дано рівняння 1. Відділення відрізків, що містять ізольований корінь. 2. Відшукання наближеного значення кореня з заданою точністю на кожному виділеному відрізку. Для відділення відрізків з ізольованим коренем, сформулюємо теорему з математичного аналізу:
Th. Якщо функція
Мал. 2.1. Мал. 2.2. Метод ітерацій. Розглянемо рівняння Нехай
Якщо це послідовність, що сходиться, то її границя є коренем рівняння (2.1). Дійсно, якщо Оскільки функція неперервна, то:
Th. Нехай функція
Похибку наближеного рішення, отриманого за методом ітерацій, визначається за формулою:
Покажемо на рисунках побудову послідовності наближених рішень за методом ітерацій.
Мал. 2.3. Наближення до кореня по "спіралі".
Мал. 2.4. Наближення до кореня по "сходам". Як видно з рисунків наближення можуть сходитися до кореня з однієї сторони (Мал.2.4) чи з двох сторін (Мал.2.3). Метод Ньютона (дотичних). Хай Хай:
Мал. 2.5. Геометрична інтерпретація методу дотичних В якості Як перше наближення
Абсциса точки перетину цієї дотичної з віссю Ох дає наближення
Th. Нехай Похибку наближеного рішення
, де
Приклад 2.1. Відділити корінь рівняння Відділимо корінь. Побудуємо графіки функцій Складемо таблицю значень: Таблиця 2.1
Мал. 2. 6. Геометричний метод відділення кореня. Як видно з рисунка, корінь рівняння укладений в інтервалі [1;2]. Перевіримо це.
Таким чином інтервал [1;2] містить принаймні один корінь. Знайдемо похідні:
Обидві похідні зберігають в інтервалі [1;2] постійний знак, отже корінь єдиний. Виберемо нульове наближення з умови
Оцінимо похибку:
Оскільки
Оскільки
Похибка першого наближення
Обчислимо друге наближення:
Оцінимо похибку другого наближення:
Метод хорд. Нехай
Проведемо хорду, що сполучає точки
Мал. 2.7. Геометрична інтерпретація методу хорд (нерухома точка Знаходимо
Абсциса точки перетину хорди з віссю Ох дає наближення
В наведеному приклад нерухомим залишався правий кінець відрізка (точка Розглянемо іншу ситуацію:
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.141 (0.027 с.) |
 невідоме точне значення деякої величини,
невідоме точне значення деякої величини,  відоме наближене значення. Величина
відоме наближене значення. Величина  називається абсолютною похибкою наближеного числа
називається абсолютною похибкою наближеного числа  .
. має назву відносної похибки
має назву відносної похибки  .
.
 , що задовольняє умові
, що задовольняє умові 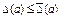
 , називається граничною абсолютною (відносною) похибкою.
, називається граничною абсолютною (відносною) похибкою.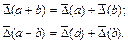

 . Необхідно знайти наближені значення коренів цього рівняння. Будемо припускати, що всі корені ізольовані, тобто кожний з коренів має окіл, що не містить інших коренів. Пошук наближених значень коренів здійснюється в 2 етапи:
. Необхідно знайти наближені значення коренів цього рівняння. Будемо припускати, що всі корені ізольовані, тобто кожний з коренів має окіл, що не містить інших коренів. Пошук наближених значень коренів здійснюється в 2 етапи: , неперервна на
, неперервна на  , має на кінцях відрізка значення протилежних знаків, тобто
, має на кінцях відрізка значення протилежних знаків, тобто  , то на
, то на  на
на 

 (2.1).
(2.1). – відрізок, що утримує єдиний корінь
– відрізок, що утримує єдиний корінь  цього рівняння. Замінимо рівняння (2.1) рівносильним:
цього рівняння. Замінимо рівняння (2.1) рівносильним:  (зручним для ітерацій) і нехай
(зручним для ітерацій) і нехай 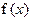 неперервна. Виберемо нульове наближення:
неперервна. Виберемо нульове наближення:  і збудуємо послідовність наближень:
і збудуємо послідовність наближень: (2.2).
(2.2).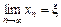 , то переходячи до границі в рівності (2.2) одержимо:
, то переходячи до границі в рівності (2.2) одержимо: 

 отже
отже  неперервне диференціюємо на
неперервне диференціюємо на  справедливо:
справедливо:  , де
, де  , то:
, то: збігається незалежно від нульового наближення.
збігається незалежно від нульового наближення.


 і функція
і функція  , неперервна на
, неперервна на  ;
; 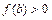 ;
;  ;
; 
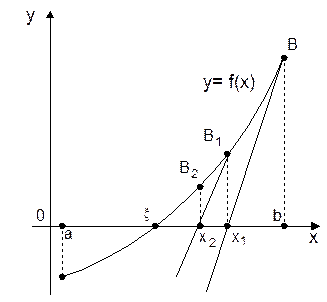
 вибираємо точку відрізка [а, b], для якої виконана умова
вибираємо точку відрізка [а, b], для якої виконана умова 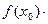
 , тобто знак функції в точці
, тобто знак функції в точці  співпадає із знаком другої похідної. (на прикладі
співпадає із знаком другої похідної. (на прикладі 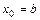 ). В точці В (
). В точці В ( ) проведемо дотичну до кривої.
) проведемо дотичну до кривої. виберемо абсцису точки перетину дотичної з віссю 0х. В точці В 1 (
виберемо абсцису точки перетину дотичної з віссю 0х. В точці В 1 ( ) проводимо дотичну і в якості
) проводимо дотичну і в якості  вибираємо абсцису точки перетину дотичної з віссю Ох і так дали. В точці Вn(
вибираємо абсцису точки перетину дотичної з віссю Ох і так дали. В точці Вn( ) проводимо дотичну:
) проводимо дотичну:
 , тобто підставляючи
, тобто підставляючи  в рівняння (2.3), отримаємо
в рівняння (2.3), отримаємо  .
.
 і
і  на відрізку
на відрізку 
 ,
,  .
. графічно і знайти наближене рішення рівняння методом дотичних з точністю e = 0.005.
графічно і знайти наближене рішення рівняння методом дотичних з точністю e = 0.005. і
і  . Абсциса точки їх перетину x- точне значення кореня.
. Абсциса точки їх перетину x- точне значення кореня.




 . Оскільки
. Оскільки  , то в якості
, то в якості  . Знаходимо перше наближення:
. Знаходимо перше наближення: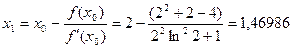

 .
.


 Оскільки похибка менше заданої точності, то
Оскільки похибка менше заданої точності, то  - шукане наближене значення кореня рівняння
- шукане наближене значення кореня рівняння  , і функція
, і функція  безперервна разом з
безперервна разом з  і
і  на
на  .
. і
і  . Як перше наближення виберемо абсцису точки перетину хорди з віссю Ох. Через точку
. Як перше наближення виберемо абсцису точки перетину хорди з віссю Ох. Через точку  і точку
і точку 
 )
) , як абсцису точки перетину хорди з віссю Ох. Будуємо точку
, як абсцису точки перетину хорди з віссю Ох. Будуємо точку  хорду
хорду  і так дали. Рівняння хорди, що проходить через точки
і так дали. Рівняння хорди, що проходить через точки  , має вигляд:
, має вигляд: (2.4)
(2.4) , отримаємо
, отримаємо  . Виразимо наближення
. Виразимо наближення 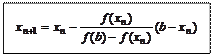
 .
.



