
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания и их характеристики. Смещение, скорость и ускорение при гармоническом колебательном движении.
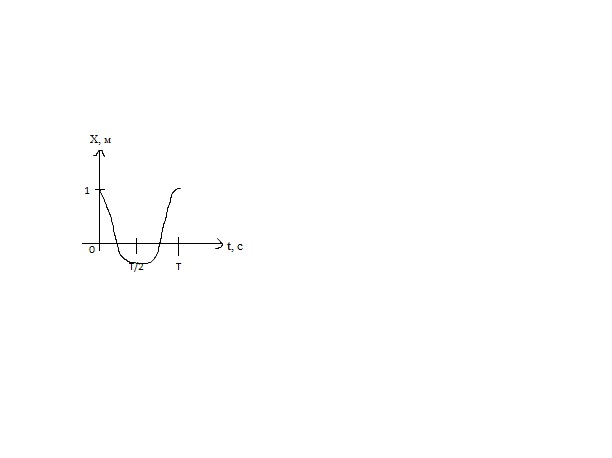
Колебание – это движение или процесс, обладающий той или иной повторяемостью от времени. В физике выделяют 3 вида колебаний: 1) механические (звук, вибрация); 2) электромагнитные (свет, радиоволны); 3) электромеханические (механические и электромагнитные вместе); Различают также колебания: Свободные – это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие): колебания груза, прикреплённого к пружине, или груза, подвешенного на нити. Вынужденные – колебания, протекающие в системе под влиянием внешнего периодического воздействия (листья на деревьях, поднятие и опускание руки). При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия. Автоколебания – колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями. Гармонические колебания – колебания, совершаемые (изменяемые) по закону синуса (кисинуса). X=Asin( X=Acos( Период колебания Т – это время, за которое фаза получает приращение 2π. [ T= v = a =
12. Дифференциальное уравнение гармонических колебаний. Пружинный, математический и физический маятники Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса): Запишем вторую производную по времени от гармонически колеблющейся величины x: Если сопоставить уравнения (1) и (2), то можно записать дифференциальное уравнение гармонических колебаний
Пружинный, физический и математический маятники 1.
 . Если на кончик пружинки прикреплен шарик массой m, то пружинка растянется под действием силы тяжести . Если на кончик пружинки прикреплен шарик массой m, то пружинка растянется под действием силы тяжести  . Возникает уравновешенная сила . Возникает уравновешенная сила  .(3) Сместим шарик еще ниже на x. Смещение станет .(3) Сместим шарик еще ниже на x. Смещение станет  . .
На шарик действует сила Если сообщить маятнику смещение 2.
Если оттолкнуть нить, то возникнет вращающий момент:
3.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.221.113 (0.006 с.) |
 t+α)
t+α)
 =
=  =-A
=-A 
 =
=  =
=  = -A
= -A  cos(
cos(


 ,
, 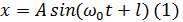 , где -смещение,А - амплитуда колебания,w0 —круговая (циклическая) частота,j —начальная фаза колебания в момент времени t=0,
, где -смещение,А - амплитуда колебания,w0 —круговая (циклическая) частота,j —начальная фаза колебания в момент времени t=0, 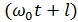 — фаза колебания в момент времени t.
— фаза колебания в момент времени t. (2).
(2). .Решением этого уравнения является функция
.Решением этого уравнения является функция  и
и  определяются начальными условиями. Все уравнения типа
определяются начальными условиями. Все уравнения типа  решаются по одному и тому же закону
решаются по одному и тому же закону  - круговая частота. Если какая–то сила действует на на колеблющее тело, то
- круговая частота. Если какая–то сила действует на на колеблющее тело, то  , где
, где  - жесткость (волновое число). Следовательно, сила пропорциональна смещению со знаком «-». Силы такого типа называется квазиупругими.
- жесткость (волновое число). Следовательно, сила пропорциональна смещению со знаком «-». Силы такого типа называется квазиупругими. Пружинный маятник — это груз массой m, подвешенный на упругой пружине и совершающий гармонические колебания под действием упругой силы F= –kx, где k —жесткость пружины.
Пружинный маятник — это груз массой m, подвешенный на упругой пружине и совершающий гармонические колебания под действием упругой силы F= –kx, где k —жесткость пружины. . С учетом (3) получаем
. С учетом (3) получаем  (квазиупругая сила).
(квазиупругая сила). , то начнутся колебания пружины: по 2-му закону Ньютона
, то начнутся колебания пружины: по 2-му закону Ньютона 
 .
. 



 .
. . Вращающий момент стремится вернуть маятник в положение равновесия. Следовательно, вращающий момент носит характер квазеупругой силы. Тогда
. Вращающий момент стремится вернуть маятник в положение равновесия. Следовательно, вращающий момент носит характер квазеупругой силы. Тогда  . Если
. Если  -малый угол, то
-малый угол, то  . Тогда, учитывая, что у нас вращательное движение, т.е. момент силы
. Тогда, учитывая, что у нас вращательное движение, т.е. момент силы  равен моменту энерции ускорения:
равен моменту энерции ускорения:  .
.  или
или  , а
, а 

 , а так как
, а так как 
 - вращающий момент,
- вращающий момент, 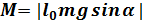 . Следовательно, вращающий момент стремится вернуть маятник в положение равновесия. Вращающий момент носит характер квазеупругой силы. Тогда
. Следовательно, вращающий момент стремится вернуть маятник в положение равновесия. Вращающий момент носит характер квазеупругой силы. Тогда  ,
,  ,
,  ,
,  .
.  (приведенная).
(приведенная). 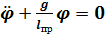 ,
,  , где
, где  .
.


