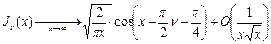Пусть в точке  расположен заряд величины
расположен заряд величины  , тогда в любой точке
, тогда в любой точке  пространства будет создаваться поле, потенциал которого:
пространства будет создаваться поле, потенциал которого:  . Для системы зарядов, потенциал имеет вид:
. Для системы зарядов, потенциал имеет вид:  .
.
 
| Диполь: Пусть в точках  и и  расположены заряды, величиной –e и +e. расположены заряды, величиной –e и +e.  - момент диполя, будем сближать точки - момент диполя, будем сближать точки  и и  , сохраняя величину , сохраняя величину  (увеличивая e), то в пределе при (увеличивая e), то в пределе при  получим точечный диполь, расположенный в точке Q, потенциал которого равен: получим точечный диполь, расположенный в точке Q, потенциал которого равен:  . .
|
Рассмотрим интеграл:  ,
,  - интегрируема (непрерывна) везде, кроме
- интегрируема (непрерывна) везде, кроме 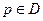 , если
, если  . Рассмотрим его сходимость и непрерывность.
. Рассмотрим его сходимость и непрерывность.
Определение: будем говорить, что это интеграл сходиться равномерно в окрестности точки  , если для любого
, если для любого  существует такое
существует такое  , (
, ( ), что для любой точки
), что для любой точки  , (
, ( - окрестность т.
- окрестность т.  ,
,  ) выполняется:
) выполняется:  .
.
Теорема: если  сходится равномерно в окрестности точки
сходится равномерно в окрестности точки  , то
, то  существует и непрерывна в точке
существует и непрерывна в точке  .
.
Доказательство: разобьём  на 2 функции:
на 2 функции:  , рассмотрим разность:
, рассмотрим разность:  (она мала, если
(она мала, если  и
и  близки).
близки).
Докажем более подробно. Поскольку  сходится в окрестности
сходится в окрестности  , то берём
, то берём  и выбираем такое
и выбираем такое  , что
, что  и
и  , тогда выполняется
, тогда выполняется  и
и  . Так как
. Так как  , то интеграл
, то интеграл  не является не собственным, и
не является не собственным, и  непрерывна в точке
непрерывна в точке  . Значит, для того же
. Значит, для того же  существует такое
существует такое  , что
, что  выполняется
выполняется  . Пусть
. Пусть  , тогда
, тогда  выполняется
выполняется  ,
,  и
и  , а следовательно и
, а следовательно и  .
.
Чтд.
Замечание: из равномерной сходимости следует сходимость интеграла.
При определении интеграла предполагалось, что промежуток интегрирования конечен и подынтегральная функция определена и непрерывна на этом промежутке. Такой интеграл называется собственным. Если нарушается хотя бы одно из этих условий, то интеграл называется несобственным.
a) Объёмный потенциал
Потенциал поля, созданного зарядами, распределёнными в области  с плотностью
с плотностью  , равен
, равен  и называется объёмным потенциалом.
и называется объёмным потенциалом.
Свойство 1. Объёмный потенциал определён и непрерывен всюду.
Если  , то интеграл
, то интеграл  не является не собственным. Поскольку подынтегральная функция, как функция
не является не собственным. Поскольку подынтегральная функция, как функция  , непрерывна в точке
, непрерывна в точке  , то непрерывен в этой точке и интеграл
, то непрерывен в этой точке и интеграл  .
.
Если 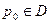 , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки  . Для этого оценим интеграл:
. Для этого оценим интеграл:  , мы увеличили область, поместив всё в шар
, мы увеличили область, поместив всё в шар  , радиуса
, радиуса  . Перейдём в последнем интеграле к сферическим координатам и получим тогда:
. Перейдём в последнем интеграле к сферическим координатам и получим тогда:  , чтобы интеграл был меньше заданного
, чтобы интеграл был меньше заданного  , достаточно взять
, достаточно взять  .
.
Свойство 2. Объёмный потенциал имеет всюду непрерывные частные производные первого порядка по координатам точки  .
.
Если  , то интеграл
, то интеграл  не является не собственным. Поскольку подынтегральная функция, как функция точки
не является не собственным. Поскольку подынтегральная функция, как функция точки  , имеет в точке
, имеет в точке  непрерывные частные производные первого порядка по координатам точки
непрерывные частные производные первого порядка по координатам точки  , то этим свойством обладает и интеграл
, то этим свойством обладает и интеграл  , причём производные вычисляются путём дифференцирования под знаком интеграла:
, причём производные вычисляются путём дифференцирования под знаком интеграла: 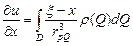 ,
,  ,
, 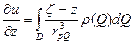 - (1), где
- (1), где  - координаты точки
- координаты точки  .
.
Если 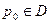 , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость в окрестностях точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость в окрестностях точки  интегралов от производных в правых частях формул. Тогда законно дифференцирование под знаком интеграла, причём для производных
интегралов от производных в правых частях формул. Тогда законно дифференцирование под знаком интеграла, причём для производных  ,
,  и
и 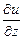 справедливы формулы (1). Для определённости рассмотрим интеграл:
справедливы формулы (1). Для определённости рассмотрим интеграл:  . Оценим его:
. Оценим его:  , т.к.
, т.к.  .
.
Далее,  , достаточно взять
, достаточно взять  для того, чтобы выполнялось неравенство
для того, чтобы выполнялось неравенство  .
.
Свойство 3. Объёмный потенциал является гармонической функцией вне области  , в которой расположены заряды (массы). Это свойство следует из того, что для точек
, в которой расположены заряды (массы). Это свойство следует из того, что для точек  интеграл
интеграл  не является не собственным, и поэтому оператор Лапласа можно вносить под знак интеграла:
не является не собственным, и поэтому оператор Лапласа можно вносить под знак интеграла:
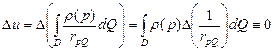 , т.к. для точек
, т.к. для точек  (а точнее P≠Q) имеем
(а точнее P≠Q) имеем  .
.
Свойство 4. в точках области  объёмный потенциал удовлетворяет соотношению:
объёмный потенциал удовлетворяет соотношению:  , т.к.
, т.к.  ,
,  .
.
Вторые производные рвутся.
Свойство 5. При стремлении точки наблюдения к бесконечности объёмный потенциал стремится к нулю ( - огр.).
- огр.).
Применим теорему о среднем:  , где
, где  - суммарный заряд. Т.о.
- суммарный заряд. Т.о.  .
.
b) Потенциал простого слоя
Потенциал поля, созданного зарядами, распределёнными по поверхности  с плотностью
с плотностью  , равен
, равен 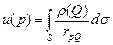 и называется потенциалом простого слоя.
и называется потенциалом простого слоя.
Свойство 1. Потенциал простого слоя определён всюду.
Если  (не принадлежит несущей поверхности
(не принадлежит несущей поверхности  ), это очевидно, т.к.
), это очевидно, т.к. 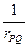 имеет конечное значение для любых р.
имеет конечное значение для любых р.
Если  , то интеграл
, то интеграл  является несобственным по двумерной области
является несобственным по двумерной области  . Из математического анализа известно, что несобственный интеграл по двумерной области
. Из математического анализа известно, что несобственный интеграл по двумерной области  абсолютно сходится, если
абсолютно сходится, если  , в нашем случае
, в нашем случае  , следовательно, интеграл сходится.
, следовательно, интеграл сходится.
Свойство 2. Потенциал простого слоя и непрерывен всюду.
Если  , то интеграл
, то интеграл 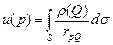 не является не собственным, и его непрерывность следует из непрерывности подынтегральной функции
не является не собственным, и его непрерывность следует из непрерывности подынтегральной функции  .
.
Если  , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки  . Для этого оценим интеграл
. Для этого оценим интеграл  по части поверхности
по части поверхности  , содержащей точку
, содержащей точку  и имеющей диаметр меньший, чем
и имеющей диаметр меньший, чем  . Пусть
. Пусть  - произвольная точка, причем:
- произвольная точка, причем:  . Пусть
. Пусть  - проекция поверхности
- проекция поверхности  на плоскость
на плоскость  , а
, а 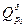 круг на плоскости
круг на плоскости  с центром в точке
с центром в точке 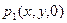 радиуса
радиуса  . Проекция на плоскость
. Проекция на плоскость  элемента поверхности
элемента поверхности  равна:
равна:  . Оценим:
. Оценим:

 вводим полярную систему координат с началом в точке
вводим полярную систему координат с началом в точке  , тогда легко вычислить последний интеграл, он равен:
, тогда легко вычислить последний интеграл, он равен: 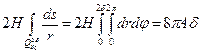 .
.
Достаточно взять  для того, чтобы выполнялось неравенство
для того, чтобы выполнялось неравенство  .
.
Свойство 3. Потенциал простого слоя является гармонической функцией всюду, кроме точек несущей поверхности  .
.
Это свойство очевидно, так как для точек  интеграл
интеграл  не является несобственным и поэтому:
не является несобственным и поэтому:

Свойство 4. нормальные производные потенциала простого слоя имеют разрыв первого рода в точках поверхности  со скачком
со скачком  .
. 
Свойство 5. если несущая поверхность  ограничена, то потенциал простого слоя стремится к нулю, когда точка
ограничена, то потенциал простого слоя стремится к нулю, когда точка  стремится к бесконечности.
стремится к бесконечности.
Применим к интегралу теорему о среднем:  , где
, где  - суммарный заряд.
- суммарный заряд.
Т.о. 
c) Потенциал двойного слоя
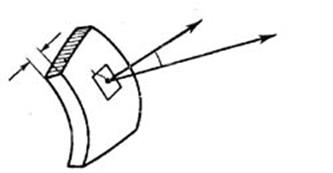
  h
h 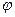 

   и и  считаем конечными. считаем конечными.
| Пусть  - двусторонняя поверхность с непрерывно меняющейся касательной плоскостью, и на ней распределены диполи с плотностью моментов - двусторонняя поверхность с непрерывно меняющейся касательной плоскостью, и на ней распределены диполи с плотностью моментов  , так, что оси их в каждой точке совпадают с положительным направлением нормали, то потенциал этого поля, созданного этими диполями: , так, что оси их в каждой точке совпадают с положительным направлением нормали, то потенциал этого поля, созданного этими диполями:  - потенциал двойного слоя. - потенциал двойного слоя.
|
Пусть  - двусторонняя поверхность с фиксированным направлением нормали. Вообразим, что в положительном направлении нормали мы отложили отрезки длинною
- двусторонняя поверхность с фиксированным направлением нормали. Вообразим, что в положительном направлении нормали мы отложили отрезки длинною  . ГМТ концов этих отрезков образуют плоскость
. ГМТ концов этих отрезков образуют плоскость  . Пусть на
. Пусть на  распределены отрицательные заряды с плотностью
распределены отрицательные заряды с плотностью  , а на
, а на  - положительные с той же плотностью. Получим «двойной слой» зарядов противоположных знаков, который можно рассматривать как совокупность диполей, распределённых по поверхностям
- положительные с той же плотностью. Получим «двойной слой» зарядов противоположных знаков, который можно рассматривать как совокупность диполей, распределённых по поверхностям  и
и  с плотностью
с плотностью  . Потенциал поля, создаваемого диполем, «опирающимся» на элементы
. Потенциал поля, создаваемого диполем, «опирающимся» на элементы  поверхностей
поверхностей  и
и  , равен
, равен  . Потенциал поля, создаваемого всеми диполями:
. Потенциал поля, создаваемого всеми диполями:  . Если устремим
. Если устремим  к нулю, то получим двойной слой на поверхности
к нулю, то получим двойной слой на поверхности  , его потенциал
, его потенциал  , а
, а  называется несущей поверхностью. Поскольку
называется несущей поверхностью. Поскольку  , то
, то 
Свойство 1. Потенциал двойного слоя определён всюду.
Свойство 2. В точках  , не лежащих на несущей поверхности
, не лежащих на несущей поверхности  , потенциал двойного слоя является гармонической функцией. Если
, потенциал двойного слоя является гармонической функцией. Если  , то этот интеграл
, то этот интеграл  не является несобственным и поэтому:
не является несобственным и поэтому:

Свойство 3. при стремлении точки наблюдения  к бесконечности потенциал двойного слоя стремится к нулю.
к бесконечности потенциал двойного слоя стремится к нулю.
Применим к  теорему о среднем:
теорему о среднем: 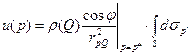 , где
, где  .
.
Свойство 4. Если плотность дипольных моментов  непрерывна на
непрерывна на  (S замкнута), то потенциал двойного слоя имеет разрыв первого рода в точках несущей поверхности
(S замкнута), то потенциал двойного слоя имеет разрыв первого рода в точках несущей поверхности  со скачком равным
со скачком равным  .
.  , где
, где  и
и  .
.
d) Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
Полученные свойства потенциалов позволяют пользоваться ими как удобным аппаратом для решения краевых задач.
Решим первую краевую задачу с уравнением Пуассона.
Задача: найти функцию, гармоническую в области  , ограниченную контуром
, ограниченную контуром  и удовлетворяющую на
и удовлетворяющую на  граничным условиям. Рассмотрим первую краевую задачу: (1)
граничным условиям. Рассмотрим первую краевую задачу: (1)  , ищем
, ищем  , дважды дифференцируемую и непрерывную в
, дважды дифференцируемую и непрерывную в  , удовлетворяющую уравнению и начальным условиям.
, удовлетворяющую уравнению и начальным условиям.
Объёмный потенциал  : внутри области
: внутри области  имеет II производную и:
имеет II производную и: 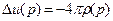 , пусть
, пусть 

 ,
,  .
.
Пусть  , причём, для
, причём, для  задача будет ставиться следующим образом: (2)
задача будет ставиться следующим образом: (2)  , задачу (1) свели к (2). Ищем её решение в виде потенциала двойного слоя:
, задачу (1) свели к (2). Ищем её решение в виде потенциала двойного слоя: 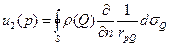 , она удовлетворяет уравнению и граничному условию (2). Таким образом, получили уравнение, которому удовлетворяет
, она удовлетворяет уравнению и граничному условию (2). Таким образом, получили уравнение, которому удовлетворяет  :
:  , из этого уравнения надо найти плотность
, из этого уравнения надо найти плотность  .
.
Таким образом, решением краевой задачи будет потенциал двойного слоя с плотностью, удовлетворяющей последнему уравнению.
e) Сводная таблица6 общие сведения о потенциалах:
| Потенциал
| Объёмный потенциал
| Потенциал простого слоя
| Потенциал двойного слоя
|
| Физическая интерпретация
| Объём  непрерывно заряжен с плотность непрерывно заряжен с плотность 
| В объёме Д находится заряженный непрерывно с плотность  лист площади S лист площади S
| В объёме Д находятся два непрерывно зараженных с плотность момента диполей  листа, сближенных по нормали: листа, сближенных по нормали:
|
| Вид потенциала
| 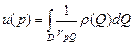
| 
| 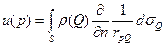
|

| Если  , то это обычные интегралы, зависящие от параметра, подынтегральное выражение нигде не обращается в бесконечность: , то это обычные интегралы, зависящие от параметра, подынтегральное выражение нигде не обращается в бесконечность:  - u гармоническая функция везде. - u гармоническая функция везде.
|

| Если  , ρ – конечно, , ρ – конечно, 
|

|  существует и непрерывен (интеграл сходиться) существует и непрерывен (интеграл сходиться)
|  существует и непрерывен существует и непрерывен
|  существует, но может быть разрывна. существует, но может быть разрывна.
|
| Первые производные:
|  существуют и непрерывны существуют и непрерывны
|  -
величины разрыва (производная рвётся) -
величины разрыва (производная рвётся)
| Говорить о них нельзя
|
| Дополнительно:
| Вторые производные:  - объёмный потенциал удовлетворяет этому соотношению в области - объёмный потенциал удовлетворяет этому соотношению в области  . .
|
| Если поверхность S замкнута, и нормаль направлена внутрь, то можно указать величину разрыва: 
|
В 2D случае всё аналогично, нужно сделать лишь следующие замены: 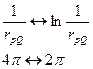
|
9. Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
Корректность - непрерывная зависимость решения от дополнительных условий в любой конечной точке области, т.е. если имеем уравнение  и два условия
и два условия  , причём
, причём  (отличные на малую величину), то и
(отличные на малую величину), то и 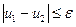 (тоже мало отличаются).
(тоже мало отличаются).
Пусть  ,
,  - гармоническая функция, тогда:
- гармоническая функция, тогда: 
 , тогда по теореме о максимумах и минимумах везде в области D верно:
, тогда по теореме о максимумах и минимумах везде в области D верно: 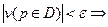
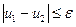
 то есть малому изменению граничных условий отвечает малое изменение решений. Задача Дирихле корректна.
то есть малому изменению граничных условий отвечает малое изменение решений. Задача Дирихле корректна.
Пример некорректной задачи:  - уравнение Лапласа. Рассмотрим задачу Коши:
- уравнение Лапласа. Рассмотрим задачу Коши:  .
.
Рассмотрим два типа начальных условий: 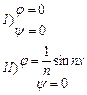 . Эти граничные условия мало отличаются при
. Эти граничные условия мало отличаются при  . Но решения не будут близкими при этом:
. Но решения не будут близкими при этом:  , т.к.
, т.к.  . Таким образом, решения будут существенно различны.
. Таким образом, решения будут существенно различны.
10. Уравнение с оператором  с особенностью
с особенностью 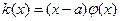 , свойства, ограниченность, постановка задачи.
, свойства, ограниченность, постановка задачи.
Теория специальных функция – это теория следующих уравнений: (*)  - линейное дифференциальное уравнение второго порядка. Пусть функция
- линейное дифференциальное уравнение второго порядка. Пусть функция  , т.е.
, т.е.  - нуль первого порядка. Решение (*) всегда:
- нуль первого порядка. Решение (*) всегда: 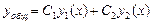 . Рассмотрим решение в окрестности особой точки, в которой
. Рассмотрим решение в окрестности особой точки, в которой  обращается в ноль.
обращается в ноль.
Теорема. Если уравнение  имеет ограниченное в точке
имеет ограниченное в точке 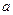 решение
решение  , то все остальные решения
, то все остальные решения  (линейно независимые) не ограничены:
(линейно независимые) не ограничены:  . То есть существует одно ограниченное решение.
. То есть существует одно ограниченное решение.
Доказательство: Из теории ОДУ знаем, что  ,
,  - Вронскиан двух решений. Докажем:
- Вронскиан двух решений. Докажем:  , тогда
, тогда  , чтд.
, чтд.
У нас  ограничено, а
ограничено, а  - нет. Рассмотрим следующую величину:
- нет. Рассмотрим следующую величину:  . Проинтегрируем эту величину:
. Проинтегрируем эту величину: 

 ,
,  , следовательно, этот интеграл расходится при
, следовательно, этот интеграл расходится при  , а это значит, что
, а это значит, что  , чтд.
, чтд.
Уточним теорему: рассмотрим два случая.
1.  в окрестности точки
в окрестности точки 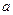 ,
, 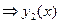 ~
~  , т.е.
, т.е.  как логарифм.
как логарифм.
2.  ~
~ 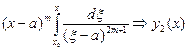 ~
~  - полюс порядка
- полюс порядка 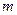 .
.
Проанализируем получившееся решение:

| Если требуется ограниченное решение в особой точке, то  , т.к. , т.к.  .
Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие. .
Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие.
|
Уравнение Бесселя.
Рассмотрим уравнение вида:  - уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,
- уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,  и
и  :
: 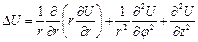 - возникает в связи с решением уравнения Лапласа в цилиндрических координатах.
- возникает в связи с решением уравнения Лапласа в цилиндрических координатах.
Решением этого уравнения (1-ым базисным решнием) является функция Бесселя первого рада:  .
.
Рассмотрим некоторые её свойства.
1) Рекуррентные соотношения. 
2) Функции Бесселя с полуцелыми номерами 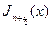 . Вычислим
. Вычислим 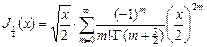 .
.
Для этого выполним преобразования: 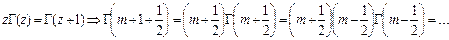
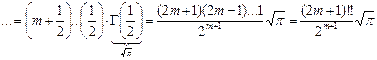 , подставим
, подставим 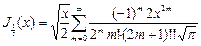 , но
, но  , тогда
, тогда  .
.
Таким образом, мы получили следующие значения: 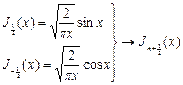 , используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.
, используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.
3) Нули функции Бесселя.
  
| 1. Они есть и их бесконечно много, следует из асимптотики:  .
2. Все нули, кроме .
2. Все нули, кроме  , простые, изолированные.
3. Все нули действительные, положительные.
4. , простые, изолированные.
3. Все нули действительные, положительные.
4.  и и  не имеют общих нулей (см. рисунок).
5. При возрастании не имеют общих нулей (см. рисунок).
5. При возрастании  корень смещается, корень смещается,  , ,  - корни функции Бесселя. - корни функции Бесселя.
|
a) особенность, построение ограниченного решения  .
.
Будем искать решение уравнения Бесселя в виде ряда Тейлора, умноженного на  :
:  . Подставим это решение в уравнение
. Подставим это решение в уравнение 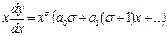 ,
,  , найдём коэффициенты и выберем ограниченное решение.
, найдём коэффициенты и выберем ограниченное решение.
Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
Пусть 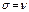 . Таким образом:
. Таким образом: 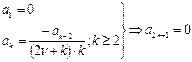 . Вычислим коэффициент
. Вычислим коэффициент  , и выразим его через
, и выразим его через  .
.
 , коэффициент
, коэффициент  выбираем произвольно:
выбираем произвольно:  , где
, где 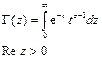 .
.
Таким образом, получили коэффициенты ряда:  , т.к.
, т.к. 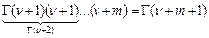 .
.
Запишем формальный ряд: 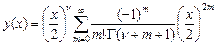 , если
, если  , тогда решение ограничено. Оно решение, т.к. ряд сходится для любых
, тогда решение ограничено. Оно решение, т.к. ряд сходится для любых  по признаку Даламбера:
по признаку Даламбера:  , сходится при всех
, сходится при всех  , радиус сходимости равен бесконечности. Таким образом, мы получили единственное, с точность до множителя решение:
, радиус сходимости равен бесконечности. Таким образом, мы получили единственное, с точность до множителя решение:  - функция Бесселя первого рода – это первое базисное решение.
- функция Бесселя первого рода – это первое базисное решение.
Случай  рассмотрен в следующем пункте.
рассмотрен в следующем пункте.
b) общее решение,  ,
,  ,
,  , понятие о функциях
, понятие о функциях 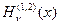 .
.
Будем искать решение уравнения Бесселя в виде ряда Тейлора, умноженного на  :
:  . Подставим это решение в уравнение
. Подставим это решение в уравнение  ,
,  , найдём коэффициенты и выберем ограниченное решение.
, найдём коэффициенты и выберем ограниченное решение.
Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
Пусть 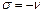 : тогда уравнение решение Бесселя будет:
: тогда уравнение решение Бесселя будет: 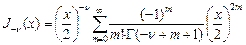 , где
, где 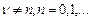 - любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения
- любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения  .
.
Пусть  - целое число, тогда
- целое число, тогда 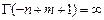 при
при  .
. 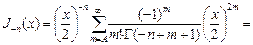 сменим индекс:
сменим индекс: 
 , получили соотношение:
, получили соотношение:  , то есть решения стали линейно зависимыми..
, то есть решения стали линейно зависимыми..
В качестве второго линейно независимого решения уравнения Бесселя можно взять функцию, построенную следующим образом: 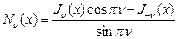 - это функция Неймана.
- это функция Неймана.
Её асимптотика 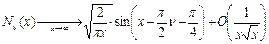 . Оно тоже может играть роль базисного уравнения.
. Оно тоже может играть роль базисного уравнения.
Могут быть и другие линейно-независимые комбинации (базисные решения):
 - функции Ханкеля, их асимптотика
- функции Ханкеля, их асимптотика  .
.
Т.о. общее решение уравнения Бесселя имеет вид (линейная комбинация 2-х базисных решений):
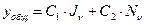
c) асимптотика решений уравнения Бесселя, нули функции Бесселя.
Функции Бесселя (любые решения уравнения Бесселя) имеют особенность в нуле. Решение уравнения Бесселя при  имеет следующий вид:
имеет следующий вид:  . Докажем это.
. Докажем это.
Для этого сделаем замену:  , подставим
, подставим 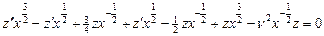 , первые производные ушли, осталось:
, первые производные ушли, осталось:  . Таким образом:
. Таким образом:  , будем искать
, будем искать 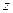 в виде:
в виде:  . Надо найти две функции:
. Надо найти две функции: 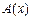 и
и  .
.
 положим
положим  , получим
, получим  . Тогда
. Тогда  , подставим в уравнение:
, подставим в уравнение:  , т.о. получили систему:
, т.о. получили систему:  . Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений:
. Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений:
 . При больших значениях
. При больших значениях  ,
, 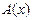 и
и  имеют вид констант.
имеют вид констант.
Получим вид 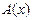 :
: 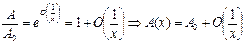 и
и  :
:  .
.
Тогда  - общая формула для любой цилиндрической функции.
- общая формула для любой цилиндрической функции.
Асимптотики функций Бесселя и Неймана:
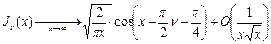


 расположен заряд величины
расположен заряд величины  , тогда в любой точке
, тогда в любой точке  пространства будет создаваться поле, потенциал которого:
пространства будет создаваться поле, потенциал которого:  . Для системы зарядов, потенциал имеет вид:
. Для системы зарядов, потенциал имеет вид:  .
.

 и
и  расположены заряды, величиной –e и +e.
расположены заряды, величиной –e и +e.  - момент диполя, будем сближать точки
- момент диполя, будем сближать точки  получим точечный диполь, расположенный в точке Q, потенциал которого равен:
получим точечный диполь, расположенный в точке Q, потенциал которого равен:  .
.
 ,
,  - интегрируема (непрерывна) везде, кроме
- интегрируема (непрерывна) везде, кроме  , если
, если  . Рассмотрим его сходимость и непрерывность.
. Рассмотрим его сходимость и непрерывность. , если для любого
, если для любого  существует такое
существует такое  , (
, ( ), что для любой точки
), что для любой точки  , (
, ( - окрестность т.
- окрестность т.  ,
,  ) выполняется:
) выполняется:  .
. сходится равномерно в окрестности точки
сходится равномерно в окрестности точки  , рассмотрим разность:
, рассмотрим разность:  (она мала, если
(она мала, если  сходится в окрестности
сходится в окрестности  и
и  , тогда выполняется
, тогда выполняется  и
и  . Так как
. Так как  , то интеграл
, то интеграл  не является не собственным, и
не является не собственным, и  , что
, что  выполняется
выполняется  . Пусть
. Пусть  , тогда
, тогда  выполняется
выполняется  .
. с плотностью
с плотностью  , равен
, равен  и называется объёмным потенциалом.
и называется объёмным потенциалом. , то интеграл
, то интеграл  не является не собственным. Поскольку подынтегральная функция, как функция
не является не собственным. Поскольку подынтегральная функция, как функция  , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки  , мы увеличили область, поместив всё в шар
, мы увеличили область, поместив всё в шар  , радиуса
, радиуса  . Перейдём в последнем интеграле к сферическим координатам и получим тогда:
. Перейдём в последнем интеграле к сферическим координатам и получим тогда:  , чтобы интеграл был меньше заданного
, чтобы интеграл был меньше заданного  , достаточно взять
, достаточно взять  .
.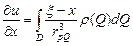 ,
,  ,
, 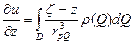 - (1), где
- (1), где  - координаты точки
- координаты точки  ,
,  и
и 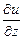 справедливы формулы (1). Для определённости рассмотрим интеграл:
справедливы формулы (1). Для определённости рассмотрим интеграл:  . Оценим его:
. Оценим его:  , т.к.
, т.к.  .
. , достаточно взять
, достаточно взять  для того, чтобы выполнялось неравенство
для того, чтобы выполнялось неравенство  .
. интеграл
интеграл 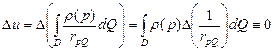 , т.к. для точек
, т.к. для точек  .
. , т.к.
, т.к.  ,
,  .
. , где
, где  - суммарный заряд. Т.о.
- суммарный заряд. Т.о.  .
. с плотностью
с плотностью 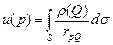 и называется потенциалом простого слоя.
и называется потенциалом простого слоя. (не принадлежит несущей поверхности
(не принадлежит несущей поверхности 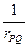 имеет конечное значение для любых р.
имеет конечное значение для любых р. , то интеграл
, то интеграл  является несобственным по двумерной области
является несобственным по двумерной области  абсолютно сходится, если
абсолютно сходится, если  , в нашем случае
, в нашем случае  , следовательно, интеграл сходится.
, следовательно, интеграл сходится. , то интеграл
, то интеграл  .
. , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки  по части поверхности
по части поверхности  , содержащей точку
, содержащей точку  . Пусть
. Пусть  - произвольная точка, причем:
- произвольная точка, причем:  . Пусть
. Пусть  - проекция поверхности
- проекция поверхности  на плоскость
на плоскость  , а
, а 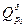 круг на плоскости
круг на плоскости 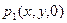 радиуса
радиуса  равна:
равна:  . Оценим:
. Оценим:
 вводим полярную систему координат с началом в точке
вводим полярную систему координат с началом в точке  , тогда легко вычислить последний интеграл, он равен:
, тогда легко вычислить последний интеграл, он равен: 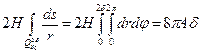 .
. для того, чтобы выполнялось неравенство
для того, чтобы выполнялось неравенство  .
. .
. интеграл
интеграл 
 .
. 
 , где
, где  - суммарный заряд.
- суммарный заряд.


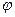


 - потенциал двойного слоя.
- потенциал двойного слоя.
 . ГМТ концов этих отрезков образуют плоскость
. ГМТ концов этих отрезков образуют плоскость  , а на
, а на  . Потенциал поля, создаваемого диполем, «опирающимся» на элементы
. Потенциал поля, создаваемого диполем, «опирающимся» на элементы  . Потенциал поля, создаваемого всеми диполями:
. Потенциал поля, создаваемого всеми диполями:  . Если устремим
. Если устремим  , то
, то 

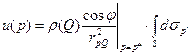 , где
, где  .
. непрерывна на
непрерывна на  (S замкнута), то потенциал двойного слоя имеет разрыв первого рода в точках несущей поверхности
(S замкнута), то потенциал двойного слоя имеет разрыв первого рода в точках несущей поверхности  .
.  , где
, где  и
и  .
. и удовлетворяющую на
и удовлетворяющую на  , ищем
, ищем  , дважды дифференцируемую и непрерывную в
, дважды дифференцируемую и непрерывную в  , удовлетворяющую уравнению и начальным условиям.
, удовлетворяющую уравнению и начальным условиям. : внутри области
: внутри области 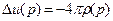 , пусть
, пусть 

 ,
,  .
. , причём, для
, причём, для  , задачу (1) свели к (2). Ищем её решение в виде потенциала двойного слоя:
, задачу (1) свели к (2). Ищем её решение в виде потенциала двойного слоя: 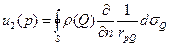 , она удовлетворяет уравнению и граничному условию (2). Таким образом, получили уравнение, которому удовлетворяет
, она удовлетворяет уравнению и граничному условию (2). Таким образом, получили уравнение, которому удовлетворяет  , из этого уравнения надо найти плотность
, из этого уравнения надо найти плотность  .
.
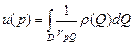

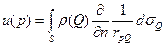

 , то это обычные интегралы, зависящие от параметра, подынтегральное выражение нигде не обращается в бесконечность:
, то это обычные интегралы, зависящие от параметра, подынтегральное выражение нигде не обращается в бесконечность:  - u гармоническая функция везде.
- u гармоническая функция везде.

 , ρ – конечно,
, ρ – конечно, 

 существуют и непрерывны
существуют и непрерывны
 -
величины разрыва (производная рвётся)
-
величины разрыва (производная рвётся)
 - объёмный потенциал удовлетворяет этому соотношению в области
- объёмный потенциал удовлетворяет этому соотношению в области 
 и два условия
и два условия  , причём
, причём  (отличные на малую величину), то и
(отличные на малую величину), то и 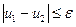 (тоже мало отличаются).
(тоже мало отличаются). ,
, 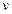 - гармоническая функция, тогда:
- гармоническая функция, тогда: 
 , тогда по теореме о максимумах и минимумах везде в области D верно:
, тогда по теореме о максимумах и минимумах везде в области D верно: 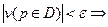
 - уравнение Лапласа. Рассмотрим задачу Коши:
- уравнение Лапласа. Рассмотрим задачу Коши:  .
.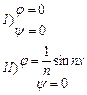 . Эти граничные условия мало отличаются при
. Эти граничные условия мало отличаются при  . Но решения не будут близкими при этом:
. Но решения не будут близкими при этом:  , т.к.
, т.к.  . Таким образом, решения будут существенно различны.
. Таким образом, решения будут существенно различны. с особенностью
с особенностью 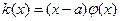 , свойства, ограниченность, постановка задачи.
, свойства, ограниченность, постановка задачи. - линейное дифференциальное уравнение второго порядка. Пусть функция
- линейное дифференциальное уравнение второго порядка. Пусть функция  , т.е.
, т.е.  - нуль первого порядка. Решение (*) всегда:
- нуль первого порядка. Решение (*) всегда: 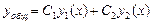 . Рассмотрим решение в окрестности особой точки, в которой
. Рассмотрим решение в окрестности особой точки, в которой  обращается в ноль.
обращается в ноль. имеет ограниченное в точке
имеет ограниченное в точке 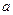 решение
решение  , то все остальные решения
, то все остальные решения  (линейно независимые) не ограничены:
(линейно независимые) не ограничены:  . То есть существует одно ограниченное решение.
. То есть существует одно ограниченное решение. ,
,  - Вронскиан двух решений. Докажем:
- Вронскиан двух решений. Докажем:  , тогда
, тогда  , чтд.
, чтд. . Проинтегрируем эту величину:
. Проинтегрируем эту величину: 
 ,
,  , следовательно, этот интеграл расходится при
, следовательно, этот интеграл расходится при  , а это значит, что
, а это значит, что  , чтд.
, чтд. в окрестности точки
в окрестности точки 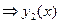 ~
~  , т.е.
, т.е.  как логарифм.
как логарифм. ~
~ 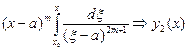 ~
~  - полюс порядка
- полюс порядка  .
.
 , т.к.
, т.к.  .
Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие.
.
Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие.
 - уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,
- уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,  и
и  :
: 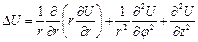 - возникает в связи с решением уравнения Лапласа в цилиндрических координатах.
- возникает в связи с решением уравнения Лапласа в цилиндрических координатах. .
.
 . Вычислим
. Вычислим 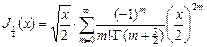 .
.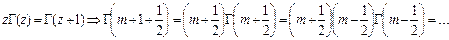
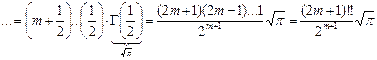 , подставим
, подставим 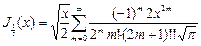 , но
, но  , тогда
, тогда  .
.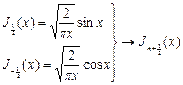 , используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.
, используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.


 .
2. Все нули, кроме
.
2. Все нули, кроме  , простые, изолированные.
3. Все нули действительные, положительные.
4.
, простые, изолированные.
3. Все нули действительные, положительные.
4.  и
и  не имеют общих нулей (см. рисунок).
5. При возрастании
не имеют общих нулей (см. рисунок).
5. При возрастании  корень смещается,
корень смещается,  ,
,  - корни функции Бесселя.
- корни функции Бесселя.
 .
. :
:  . Подставим это решение в уравнение
. Подставим это решение в уравнение 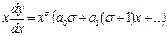 ,
,  , найдём коэффициенты и выберем ограниченное решение.
, найдём коэффициенты и выберем ограниченное решение. :
: 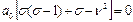 При
При 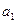 :
: 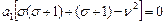 При
При  :
:  При
При  :
: 


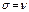 . Таким образом:
. Таким образом: 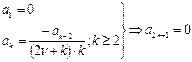 . Вычислим коэффициент
. Вычислим коэффициент  , и выразим его через
, и выразим его через  .
. , коэффициент
, коэффициент  выбираем произвольно:
выбираем произвольно:  , где
, где 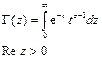 .
. , т.к.
, т.к. 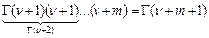 .
.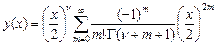 , если
, если  , тогда решение ограничено. Оно решение, т.к. ряд сходится для любых
, тогда решение ограничено. Оно решение, т.к. ряд сходится для любых  по признаку Даламбера:
по признаку Даламбера:  , сходится при всех
, сходится при всех  - функция Бесселя первого рода – это первое базисное решение.
- функция Бесселя первого рода – это первое базисное решение. рассмотрен в следующем пункте.
рассмотрен в следующем пункте. ,
,  , понятие о функциях
, понятие о функциях 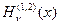 .
. ,
, 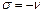 : тогда уравнение решение Бесселя будет:
: тогда уравнение решение Бесселя будет: 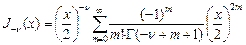 , где
, где 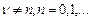 - любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения
- любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения 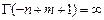 при
при  .
. 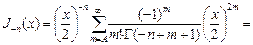 сменим индекс:
сменим индекс: 
 , получили соотношение:
, получили соотношение:  , то есть решения стали линейно зависимыми..
, то есть решения стали линейно зависимыми..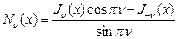 - это функция Неймана.
- это функция Неймана.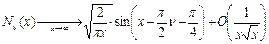 . Оно тоже может играть роль базисного уравнения.
. Оно тоже может играть роль базисного уравнения. - функции Ханкеля, их асимптотика
- функции Ханкеля, их асимптотика  .
.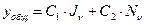
 имеет следующий вид:
имеет следующий вид:  . Докажем это.
. Докажем это. , подставим
, подставим 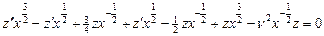 , первые производные ушли, осталось:
, первые производные ушли, осталось:  . Таким образом:
. Таким образом:  , будем искать
, будем искать 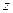 в виде:
в виде:  . Надо найти две функции:
. Надо найти две функции: 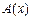 и
и  .
. положим
положим  , получим
, получим  . Тогда
. Тогда  , подставим в уравнение:
, подставим в уравнение:  , т.о. получили систему:
, т.о. получили систему:  . Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений:
. Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений: . При больших значениях
. При больших значениях 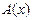 и
и  имеют вид констант.
имеют вид констант.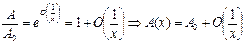 и
и  :
:  .
. - общая формула для любой цилиндрической функции.
- общая формула для любой цилиндрической функции.