
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о среднем для гармонических функций
Теорема о среднем: Для любой гармонической функции Доказательство: запишем интегральную формулу: Учтём что, Чтд. Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле. Теорема о максимумах и минимумах. Любая функция, гармоническая в области D и непрерывная на Г принимает своё максимальное и минимальное значения на границах и только на границах (за исключением тривиального случая U = const). Доказательство: пусть теорема не верна. Вычтем: Чтд. Теорема о минимумах доказывается аналогично, заменой (u) на (-u). Следствия: 1. Единственность. Задача Дирихле имеет единственное решение, если её однородная задача имеет только тривиально решение. Рассмотрим первую краевую задачу Дирихле. 2. Корректность - непрерывная зависимость решений от дополнительных условий в любой конечной точке области. Если имеем уравнение Пусть
Пример некорректной задачи: Рассмотрим два типа начальных условий:
|
|||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.8.247 (0.005 с.) |
 в области D выполняется:
в области D выполняется: 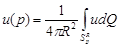 - равна своему среднему значению по любой сфере с центром в точке р и радиусом R -
- равна своему среднему значению по любой сфере с центром в точке р и радиусом R -  .
.
 . Функция
. Функция  . Последний интеграл исчез. Воспользуемся первым свойством гармонических функций: интеграл по любой замкнутой поверхности внутри области гармоничности D равен нулю. Тогда получаем что,
. Последний интеграл исчез. Воспользуемся первым свойством гармонических функций: интеграл по любой замкнутой поверхности внутри области гармоничности D равен нулю. Тогда получаем что,  . Первый интеграл исчез. Рассмотрим второй интеграл, учтём, что производная по нормали совпадает с производной по радиусу:
. Первый интеграл исчез. Рассмотрим второй интеграл, учтём, что производная по нормали совпадает с производной по радиусу:  .
. - максимум достигается во внутренней точке. Применим теорему о среднем:
- максимум достигается во внутренней точке. Применим теорему о среднем:  , видим, что:
, видим, что:  .
. , но
, но  значит что разность
значит что разность  всегда, а
всегда, а  от неотрицательной непрерывной функции равен нулю в случае если
от неотрицательной непрерывной функции равен нулю в случае если  на сфере
на сфере  , то есть получили, что максимум достигается на границе сферы
, то есть получили, что максимум достигается на границе сферы  . Пусть задача Дирихле имеет два решения:
. Пусть задача Дирихле имеет два решения:  , тогда:
, тогда:  из теоремы о mах и min следует, что
из теоремы о mах и min следует, что  - во всей области D в том числе и на границе.
- во всей области D в том числе и на границе. и два условия
и два условия  , причём
, причём  (отличные на малую величину), то и
(отличные на малую величину), то и 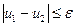 (тоже мало отличаются). Докажем.
(тоже мало отличаются). Докажем. ,
, 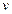 - гармоническая функция, тогда:
- гармоническая функция, тогда: 
 , тогда по теореме о максимумах и минимумах везде в области D верно:
, тогда по теореме о максимумах и минимумах везде в области D верно: 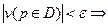
 то есть малому изменению граничных условий отвечает малое изменение решений. Задача Дирихле корректна.
то есть малому изменению граничных условий отвечает малое изменение решений. Задача Дирихле корректна. - уравнение Лапласа. Рассмотрим задачу Коши:
- уравнение Лапласа. Рассмотрим задачу Коши:  .
.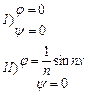 . Эти граничные условия мало отличаются при
. Эти граничные условия мало отличаются при  . Но решения не будут близкими при этом:
. Но решения не будут близкими при этом:  , т.к.
, т.к.  . Таким образом, решения будут различны при больших n.
. Таким образом, решения будут различны при больших n.


