Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Лапласа и Пуассона.Стр 1 из 5Следующая ⇒
Оглавление
Оглавление. 1 1. Уравнение Лапласа и Пуассона. 2 a)Физический смысл стационарной задачи. 2 b)Примеры.. 2 c)Понятие о потенциалах. 2 d)Постановка задач. 2 2. Первая и вторая формулы Грина с оператором 3. Гармонические функции. Интегральное представление. Их основные свойства. 4 4. Теорема о среднем для гармонических функций.. 6 5. Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле. 7 6. Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений. 8 7. Функция Грина для задачи с уравнением a)решение задач с её помощью.. 9 b)построение в одномерном случае на отрезке. 9 8. Теория потенциалов, определение, основные свойства. 11 a)Объёмный потенциал. 12 b)Потенциал простого слоя. 14 c)Потенциал двойного слоя. 15 d)Решение задач Дирихле с уравнением Пуассона методом теории потенциалов. 16 e)Сводная таблица6 общие сведения о потенциалах: 17 9. Понятие о корректно и некорректно поставленных задачах математической физики, примеры. 18 10.Уравнение с оператором 11.Уравнение Бесселя. 20 a) особенность, построение ограниченного решения b) общее решение, c)асимптотика решений уравнения Бесселя, нули функции Бесселя. 23 d)краевая задача на собственные значения: e) модифицированное уравнение Бесселя, ограниченность решения f)Сводная таблица. 26 12.Краевая задача 13.Уравнение гипергеометрического типа. 28 a)Приведение к самосопряжённому виду. Весовые функции b)Решение в виде полиномов. Формула Родрига. 29 c)Ортогональные решения полиномов.Свойства нулей. 30 14.Примеры: уравнения, краевые задачи, определение и свойства полиномов. 31 a)Лежандра. 31 b)Чебышева-Лягера. 32 c)Чебышева-Эрмита. 33 d)Сводная таблица для уравнений гипергеометрического вида. 34 15.Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства. 36
16.Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных. 37 17.Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д. 38 Гармонические функции. Интегральное представление. Их основные свойства.
Примеры 1: Линейная функция вида 2: Цилиндрические функции. Рассмотрим цилиндрическую систему координат (r,φ,z): 3: Сферические функции. Рассмотрим сферические координаты: Получим формулу интегрального представления. Пусть Рассмотрим последний интеграл: Применим к первому слагаемому теорему о среднем: (Примечание: когда мы окружали окрестностью Таким образом, получили, что: В двумерном случае получаем аналогично:
Чтд. Уравнение Бесселя. Рассмотрим уравнение вида:
Решением этого уравнения (1-ым базисным решнием) является функция Бесселя первого рада: Рассмотрим некоторые её свойства. 1) Рекуррентные соотношения. 2) Функции Бесселя с полуцелыми номерами Для этого выполним преобразования:
Таким образом, мы получили следующие значения: 3) Нули функции Бесселя.
a) особенность, построение ограниченного решения Будем искать решение уравнения Бесселя в виде ряда Тейлора, умноженного на Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
Пусть
Таким образом, получили коэффициенты ряда: Запишем формальный ряд: Случай b) общее решение, Будем искать решение уравнения Бесселя в виде ряда Тейлора, умноженного на Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
Пусть Пусть В качестве второго линейно независимого решения уравнения Бесселя можно взять функцию, построенную следующим образом: Её асимптотика Могут быть и другие линейно-независимые комбинации (базисные решения):
Т.о. общее решение уравнения Бесселя имеет вид (линейная комбинация 2-х базисных решений):
c) асимптотика решений уравнения Бесселя, нули функции Бесселя. Функции Бесселя (любые решения уравнения Бесселя) имеют особенность в нуле. Решение уравнения Бесселя при Для этого сделаем замену:
Получим вид Тогда Асимптотики функций Бесселя и Неймана:
d) краевая задача на собственные значения: Рассмотрим краевую задачу на собственные значения. Первое решение: - тождественный ноль, а задача Штурма-Лиувилля – это задача на собственные функции и собственные значения - заключается в нахождении таких значений Сделаем замену: Все собственные значения действительны и положительны. Это следует из самосопряженности оператора
Все собственные функции, отвечающие разным собственным значениям ортогональны с весом Теорема Фурье-Бесселя (о полноте) Любая функция В задаче на собственные функции и собственные значения всё будет аналогично, если вместо краевого условие первого рода мы возьмём e) модифицированное уравнение Бесселя, ограниченность решения Рассмотрим уравнение: В качестве С возьмем
f) Сводная таблица.
12. Краевая задача Рассмотрим уравнение: (*)
Полученные функции, отвечающие различным собственным значениям, будут ортогональны, то есть оператор Самосопряженность оператора Используя 2-ую формулу Грина получаем: Примеры: уравнения, краевые задачи, определение и свойства полиномов a) Полиномы Лежандра. 1) Определим многочлены Лежандра так: разложим в ряд по степеням Коэффициенты этого разложения 2) Краевая задача: найти такие значения Функция Упрощённое уравнение Лежандра: 3) Рекуррентные соотношения: 4) Ортогональность и норма полиномов Лежандра: 5) Все нули полиномов Лежандра простые и расположены на интервале 6) Ограниченность: полиномы Лежандра b) Полиномы Чебышева-Лягера. 1) Определим полиномы Чебышева-Лягера так: разложим в ряд по степеням
Коэффициенты этого разложения 2) Краевая задача: найти такие значения Функция Упрощённое уравнение Чебышева-Лягера: 3) Рекуррентные соотношения: 4) Ортогональность и норма полиномов Чебышева-Лягера:
c) Чебышева-Эрмита. 1) Определим полиномы Чебышева-Эрмита так: разложим в ряд по степеням Коэффициенты этого разложения 2) Краевая задача: найти такие значения Функция Упрощённое уравнение Чебышева-Эрмита: 3) Рекуррентные соотношения: 4) Ортогональность и норма полиномов Чебышева-Эрмита:
d) Сводная таблица для уравнений гипергеометрического вида.
Оглавление
Оглавление. 1 1. Уравнение Лапласа и Пуассона. 2 a)Физический смысл стационарной задачи. 2 b)Примеры.. 2 c)Понятие о потенциалах. 2 d)Постановка задач. 2 2. Первая и вторая формулы Грина с оператором 3. Гармонические функции. Интегральное представление. Их основные свойства. 4 4. Теорема о среднем для гармонических функций.. 6 5. Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле. 7 6. Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений. 8 7. Функция Грина для задачи с уравнением a)решение задач с её помощью.. 9 b)построение в одномерном случае на отрезке. 9 8. Теория потенциалов, определение, основные свойства. 11 a)Объёмный потенциал. 12 b)Потенциал простого слоя. 14 c)Потенциал двойного слоя. 15 d)Решение задач Дирихле с уравнением Пуассона методом теории потенциалов. 16 e)Сводная таблица6 общие сведения о потенциалах: 17 9. Понятие о корректно и некорректно поставленных задачах математической физики, примеры. 18 10.Уравнение с оператором 11.Уравнение Бесселя. 20
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.112.111 (0.126 с.) |
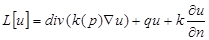 , следствия. 3
, следствия. 3 , понятия, определения. 9
, понятия, определения. 9 с особенностью
с особенностью 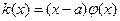 , свойства, ограниченность, постановка задачи. 19
, свойства, ограниченность, постановка задачи. 19 . 21
. 21 ,
,  , понятие о функциях
, понятие о функциях 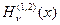 . 22
. 22 , её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д. 24
, её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д. 24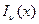 , свойства, общее решение, понятие о функции
, свойства, общее решение, понятие о функции  . 25
. 25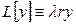 с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора
с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора 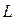 . 27
. 27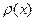 . Уравнение для производных. 28
. Уравнение для производных. 28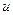 (p) - гармоническая функция – если она удовлетворяет уравнению Лапласа:
(p) - гармоническая функция – если она удовлетворяет уравнению Лапласа:  ,
, 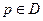 и непрерывна в
и непрерывна в  .
.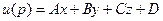 - гармоническая функция, т.к. удовлетворяет условиям.
- гармоническая функция, т.к. удовлетворяет условиям. и
и 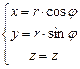 , тогда
, тогда  , если
, если  , то останется первое слагаемое:
, то останется первое слагаемое: 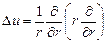 =0, решаем
=0, решаем 
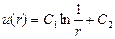 . Т.о. функция вида
. Т.о. функция вида 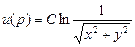 - гармоническая функция в т.
- гармоническая функция в т.  .
. и
и 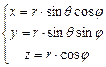 , тогда
, тогда  , если
, если  , решаем т.о. функция вида
, решаем т.о. функция вида  - гармоническая функция в т.
- гармоническая функция в т.  , тогда (согласно второй формуле Грина) получаем:
, тогда (согласно второй формуле Грина) получаем:  . Эта формула верна в случае любых двух непрерывно дифференцируемых функций в области D, а
. Эта формула верна в случае любых двух непрерывно дифференцируемых функций в области D, а 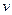 выбираем следующим образом:
выбираем следующим образом: 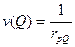 , (причём заметим, что
, (причём заметим, что  - гармоническая функция),
- гармоническая функция),  -
-  . Т.о. формула справедлива в области
. Т.о. формула справедлива в области  и появится ещё одно слагаемое:
и появится ещё одно слагаемое: 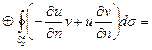 - интеграл по сфере
- интеграл по сфере 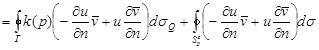 .
.
 ,
,  - точка на сфере
- точка на сфере 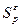 . Перейдём к переделу
. Перейдём к переделу  :
:  - первое слагаемое исчезло. Рассмотрим второе слагаемое:
- первое слагаемое исчезло. Рассмотрим второе слагаемое:  применим теорему о среднем
применим теорему о среднем  ,
,  - точка на сфере
- точка на сфере  :
: 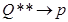 . Второе слагаемое:
. Второе слагаемое:  . Тогда второй интеграл перепишется в виде:
. Тогда второй интеграл перепишется в виде: 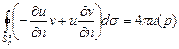 , а интеграл
, а интеграл  , так как
, так как  .
. ).
). , выражаем
, выражаем  . Мы получили формулу для 3D случая (к(р) положим = 1):
. Мы получили формулу для 3D случая (к(р) положим = 1):  .
. ,
, - расстояние между точками p и Q.
- расстояние между точками p и Q. - уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,
- уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,  и
и  :
: 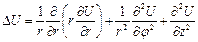 - возникает в связи с решением уравнения Лапласа в цилиндрических координатах.
- возникает в связи с решением уравнения Лапласа в цилиндрических координатах. .
.
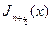 . Вычислим
. Вычислим 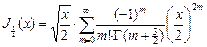 .
.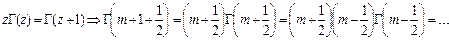
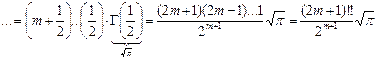 , подставим
, подставим 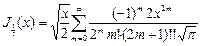 , но
, но  , тогда
, тогда  .
.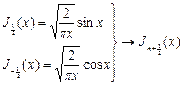 , используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.
, используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.


 .
2. Все нули, кроме
.
2. Все нули, кроме  , простые, изолированные.
3. Все нули действительные, положительные.
4.
, простые, изолированные.
3. Все нули действительные, положительные.
4. 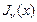 и
и  не имеют общих нулей (см. рисунок).
5. При возрастании
не имеют общих нулей (см. рисунок).
5. При возрастании  корень смещается,
корень смещается, 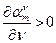 ,
,  - корни функции Бесселя.
- корни функции Бесселя.
 :
:  . Подставим это решение в уравнение
. Подставим это решение в уравнение 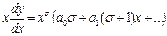 ,
,  , найдём коэффициенты и выберем ограниченное решение.
, найдём коэффициенты и выберем ограниченное решение. :
: 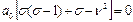 При
При 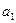 :
: 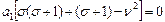 При
При  :
:  При
При  :
: 


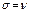 . Таким образом:
. Таким образом: 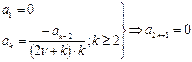 . Вычислим коэффициент
. Вычислим коэффициент  , и выразим его через
, и выразим его через  .
. , коэффициент
, коэффициент  выбираем произвольно:
выбираем произвольно:  , где
, где 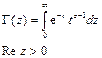 .
. , т.к.
, т.к. 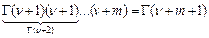 .
.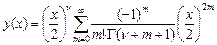 , если
, если  , тогда решение ограничено. Оно решение, т.к. ряд сходится для любых
, тогда решение ограничено. Оно решение, т.к. ряд сходится для любых 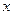 по признаку Даламбера:
по признаку Даламбера:  , сходится при всех
, сходится при всех  - функция Бесселя первого рода – это первое базисное решение.
- функция Бесселя первого рода – это первое базисное решение. рассмотрен в следующем пункте.
рассмотрен в следующем пункте. ,
, 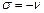 : тогда уравнение решение Бесселя будет:
: тогда уравнение решение Бесселя будет: 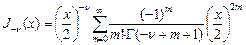 , где
, где 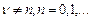 - любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения
- любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения 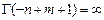 при
при  .
. 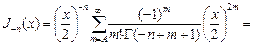 сменим индекс:
сменим индекс: 
 , получили соотношение:
, получили соотношение:  , то есть решения стали линейно зависимыми..
, то есть решения стали линейно зависимыми..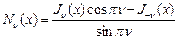 - это функция Неймана.
- это функция Неймана.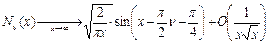 . Оно тоже может играть роль базисного уравнения.
. Оно тоже может играть роль базисного уравнения. - функции Ханкеля, их асимптотика
- функции Ханкеля, их асимптотика  .
.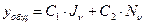
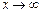 имеет следующий вид:
имеет следующий вид:  . Докажем это.
. Докажем это. , подставим
, подставим 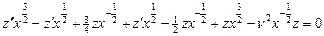 , первые производные ушли, осталось:
, первые производные ушли, осталось:  . Таким образом:
. Таким образом:  , будем искать
, будем искать 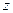 в виде:
в виде:  . Надо найти две функции:
. Надо найти две функции: 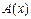 и
и  .
. положим
положим  , получим
, получим  . Тогда
. Тогда  , подставим в уравнение:
, подставим в уравнение:  , т.о. получили систему:
, т.о. получили систему:  . Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений:
. Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений: . При больших значениях
. При больших значениях 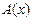 и
и  имеют вид констант.
имеют вид констант.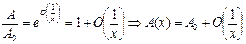 и
и  :
:  .
. - общая формула для любой цилиндрической функции.
- общая формула для любой цилиндрической функции.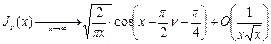
 , её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
, её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д. 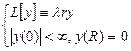 на отрезке
на отрезке  , или:
, или:  , отличается от уравнения Бесселя наличием параметра
, отличается от уравнения Бесселя наличием параметра  .
. , (
, ( )
) 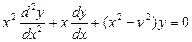 , его общее решение
, его общее решение 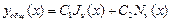 , константы находим из начального условия. Из ограниченности
, константы находим из начального условия. Из ограниченности  находим, что
находим, что  , из второго условия
, из второго условия  находим что:
находим что:  - это уравнение для определения
- это уравнение для определения  бесконечно много нулей:
бесконечно много нулей:  , тогда можно написать, что
, тогда можно написать, что  . Тогда собственные значения
. Тогда собственные значения  - их бесконечно много, и соответственно собственные функции
- их бесконечно много, и соответственно собственные функции  .
. . Убедимся в его самосопряженности. Напишем формулу Грина
. Убедимся в его самосопряженности. Напишем формулу Грина ,
,  - т.е. оператор самосопряжённый. Это значит, что все собственные значения действительны и положительны, т.к.
- т.е. оператор самосопряжённый. Это значит, что все собственные значения действительны и положительны, т.к.  и
и 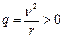 .
.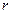 :
: 
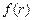 , которая на отрезке
, которая на отрезке  , разлагается в абсолютно и равномерно сходящийся ряд по функциям Бесселя:
, разлагается в абсолютно и равномерно сходящийся ряд по функциям Бесселя:  . Коэффициенты находятся интегрированием, т.к. это разложение по ортогональному базису.
. Коэффициенты находятся интегрированием, т.к. это разложение по ортогональному базису. 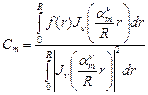 .
.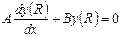 , тогда
, тогда 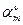 - будут корнями уравнения:
- будут корнями уравнения:  .
. , оно отличается знаком перед
, оно отличается знаком перед  . Сделаем замену
. Сделаем замену  , тогда подставим и получим уравнение:
, тогда подставим и получим уравнение:  , получили уравнение Бесселя. Его ограниченное решение:
, получили уравнение Бесселя. Его ограниченное решение: 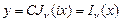 - модифицированная функция Бесселя.
- модифицированная функция Бесселя. , тогда
, тогда  . Он отличается знакопостоянством. Рассмотрим его асимптотику:
. Он отличается знакопостоянством. Рассмотрим его асимптотику:  . Модифицированная функция заведомо не имеет нулей (только на мнимой оси), т.к. все слагаемые положительные. Напишем базис. Первая базисная функция -
. Модифицированная функция заведомо не имеет нулей (только на мнимой оси), т.к. все слагаемые положительные. Напишем базис. Первая базисная функция -  , вторая базисная функция -
, вторая базисная функция - 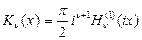 - функция Макдональда.
- функция Макдональда.  - действительна для действительных
- действительна для действительных 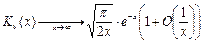 , тогда общее решение можно записать так:
, тогда общее решение можно записать так:  . Из линейной независимости
. Из линейной независимости 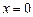 имеет полюс
имеет полюс 
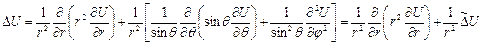

 (асимптотика):
(асимптотика):

 ;
; 

 ;
; 
 ;
; 



 2)
2) 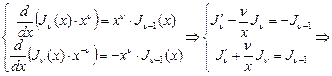

 ;
; 

 , где
, где 
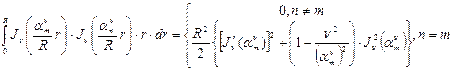
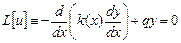 и пусть
и пусть  - имеет два ноля.
- имеет два ноля.
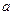 перейдёт в ограниченное решение в точке
перейдёт в ограниченное решение в точке 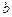 :
: 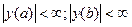 . Но в общем случае всё множество решения, как правило, неограниченно. Исключительная ситуация может быть в случае нулевого решения. Таким образом возникает задача нахождения таких собственных значений λ, при которых задача -
. Но в общем случае всё множество решения, как правило, неограниченно. Исключительная ситуация может быть в случае нулевого решения. Таким образом возникает задача нахождения таких собственных значений λ, при которых задача -  при
при  - имеет нетривиальное решение; роль граничных условий здесь играет требование на ограниченность решения
- имеет нетривиальное решение; роль граничных условий здесь играет требование на ограниченность решения 
 должен быть самосопряжённым.
должен быть самосопряжённым.
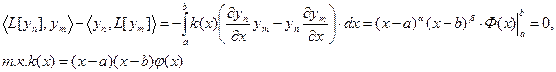
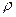 функцию:
функцию: 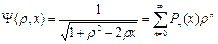 .
.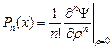 являются многочленами, называемыми полиномами Лежандра.
являются многочленами, называемыми полиномами Лежандра. 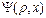 - называется производящей функцией полиномов Лежандра.
- называется производящей функцией полиномов Лежандра.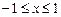 существуют не тривиальные решения уравнения Лежандра
существуют не тривиальные решения уравнения Лежандра 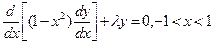 , ограниченные при
, ограниченные при  .
.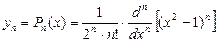 - есть собственная функция задачи, соответствующая собственному значению
- есть собственная функция задачи, соответствующая собственному значению 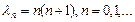 .
.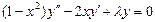
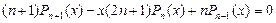
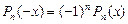
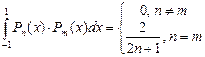 , полиномы Лежандра разных порядков ортогональны между собой; второе линейно независимое решение уравнения Лежандра при
, полиномы Лежандра разных порядков ортогональны между собой; второе линейно независимое решение уравнения Лежандра при 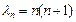 обращается в бесконечность при
обращается в бесконечность при  .
.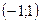 .
.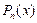 равномерно ограниченны для всех значений аргумента
равномерно ограниченны для всех значений аргумента 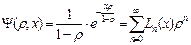 .
.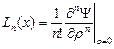 являются многочленами, называемыми полиномами Чебышева-Лягера.
являются многочленами, называемыми полиномами Чебышева-Лягера. 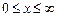 существуют не тривиальные решения уравнения Чебышева-Лягера
существуют не тривиальные решения уравнения Чебышева-Лягера 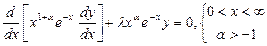 , ограниченные при
, ограниченные при 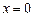 и возрастающие при
и возрастающие при 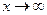 не быстрее чем конечная степень
не быстрее чем конечная степень 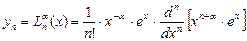 - есть собственная функция задачи, соответствующая собственному значению
- есть собственная функция задачи, соответствующая собственному значению 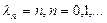 .
.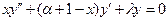
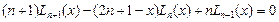
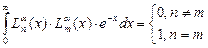 :, полиномы Чебышева-Лягера разных порядков ортогональны между собой с весом
:, полиномы Чебышева-Лягера разных порядков ортогональны между собой с весом 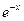 .
.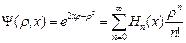 .
.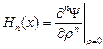 являются многочленами, называемыми полиномами Лежандра.
являются многочленами, называемыми полиномами Лежандра.  существуют не тривиальные решения уравнения Чебышева-Эрмита
существуют не тривиальные решения уравнения Чебышева-Эрмита 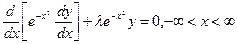 , возрастающее при
, возрастающее при  не быстрее чем конечная степень
не быстрее чем конечная степень 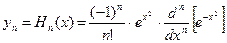 - есть собственная функция задачи, соответствующая собственному значению
- есть собственная функция задачи, соответствующая собственному значению 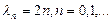 .
.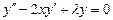
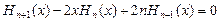 ;
; 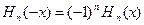
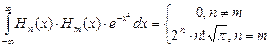 , полиномы Чебышева-Эрмита разных порядков ортогональны на
, полиномы Чебышева-Эрмита разных порядков ортогональны на 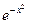 между собой.
между собой.
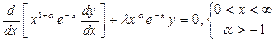
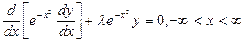
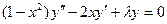

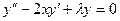
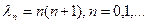
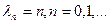
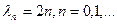

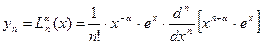
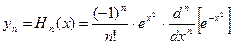


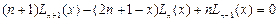
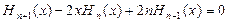
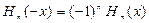

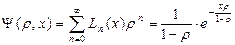
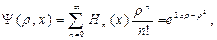
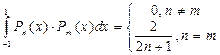
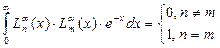
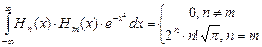
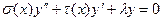
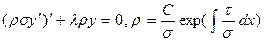
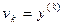
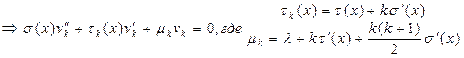
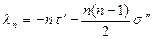
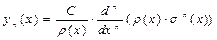

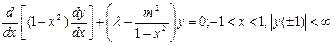
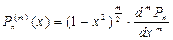 ,
,